关键路径——C语言（代码）

上一篇文章讲了关键路径的理论部分，今天这篇文章讲一下如何实现关键路径。

首先我们有这样一个图，先要构建好图：

        然后构建关键路径函数，上篇文章我们说到我们要先拓扑排序，接着计算最早最晚开始时间，所以在函数的开始部分，我们要为拓扑排序的序列，最早开始时间和最晚开始时间开辟数组，并且进行初始化。

	int* top = (int*)malloc(sizeof(int) * G->vexsNum);
	int* early = (int*)malloc(sizeof(int) * G->vexsNum);
	int* late = (int*)malloc(sizeof(int) * G->vexsNum);
	top=toposort(G, S);
	for (int i = 0; i < G->vexsNum; i++) {
		early[i] = 0;
		late[i] = 0;
	}

        然后我们要来计算事件的最早开始和最晚开始时间，首先要遍历每两个事件之间的活动，得到活动的最大值（计算最早开始时间，因为要考虑事件前驱的所有活动都完成）：

	for (int i = 0; i < G->vexsNum; i++) {
		for (int j = 0; j < G->vexsNum; j++) {
        遍历每两个事件间的活动
		}
	}

        遍历活动也是有顺序的，要先遍历拓扑排序指向最靠前的事件的活动，然后依次遍历，如图所示：先遍历指向首个事件的活动，但是没有，所以事件0的最早开始时间就是0。

        接着遍历下一个事件（因为我的拓扑排序使用的是栈，所以第二个是事件3）事件 3 的前驱只有一个活动C，所以最早开始时间就是 early[3]=early[0]+G->[0][3]，同理，事件1最早开始时间为6，事件2最早开始时间为4。

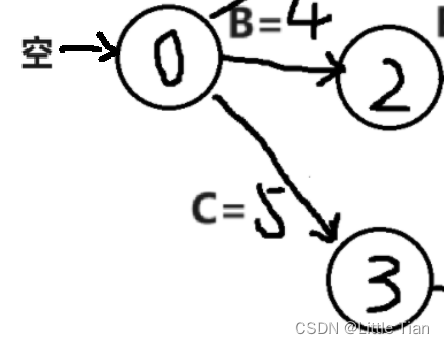
        接着是事件4，此时early[1]+G->[1][4]=7，early[2]+G->[2][4]=5，因为要求最早开始时间就是7，所以这也说明我们要在遍历中找最大值。

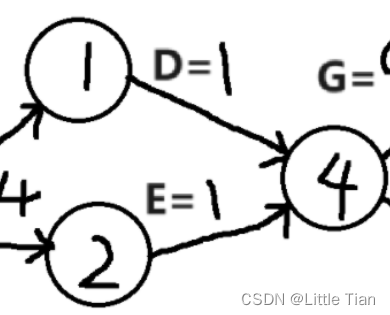
大概的思路已经有了

	for (int i = 0; i < G->vexsNum; i++) {
        int max=0;
		for (int j = 0; j < G->vexsNum; j++) {
        取得拓扑排序的最先事件index
        if(指向index的活动！=Max 并且 指向index的活动！=0 并且 ——————
         ——————指向index的活动+指向index的事件的最早开始时间>Max){
                更新Max；
        }

		}
        更新early数组
	}

最后的代码如下，if条件很长，所以写成了两个if。这里要注意是top[i]而不是i，表示拓扑序列中的第一个事件。

	for (int i = 0; i < G->vexsNum; i++) {
		int max = 0;
		for (int j = 0; j < G->vexsNum; j++) {
			if (G->arcs[j][top[i]] != 0 && G->arcs[j][top[i]] < Max) {
				if (G->arcs[j][top[i]] + early[j] > max) {
					max = G->arcs[j][top[i]] + early[j];
				}
			}
		}
		early[top[i]] = max;
		printf("%d ", early[top[i]]);
	}

        这样我们就计算出了事件的最早开始时间。

        最晚开始时间时间的计算类似，只不过因为我们要从后往前推，所以需要先设置好最后一个最晚开始时间。接着后继事件的最晚开始时间减去活动时间（最小的那个）就是该事件的最晚开始时间。

    late[G->vexsNum - 1] = early[G->vexsNum - 1];
	for (int i = G->vexsNum - 2; i >= 0;i--) {
		int min = Max;
		for (int j = 0; j < G->vexsNum; j++) {
			if (G->arcs[top[i]][j] != 0 && G->arcs[top[i]][j] < Max) {
				if (late[j] - G->arcs[top[i]][j] < min) {
					min = late[j] - G->arcs[top[i]][j];
				}
			}
		}
		late[top[i]] = min;
		printf("%d ", late[top[i]]);
	}

        以上就是事件的最早最晚开始时间的计算。

关键路径就是当early数组和late数组相等时的事件连成的路径，

    for (int i = 0; i < G->vexsNum; i++) {
        if (early[i] == late[i]) {
            printf("%d ", i);
        }
    }

最后的代码为： 

void calculateCriticalPath(Graph* G,StackNode* S ) {
	int* top = (int*)malloc(sizeof(int) * G->vexsNum);
	int* early = (int*)malloc(sizeof(int) * G->vexsNum);
	int* late = (int*)malloc(sizeof(int) * G->vexsNum);
	top=toposort(G, S);
	for (int i = 0; i < G->vexsNum; i++) {
		early[i] = 0;
		late[i] = 0;
	}
	for (int i = 0; i < G->vexsNum; i++) {
		int max = 0;
		for (int j = 0; j < G->vexsNum; j++) {
			if (G->arcs[j][top[i]] != 0 && G->arcs[j][top[i]] < Max) {
				if (G->arcs[j][top[i]] + early[j] > max) {
					max = G->arcs[j][top[i]] + early[j];
				}
			}
		}
		early[top[i]] = max;
		printf("%d ", early[top[i]]);
	}

	printf("\n");

	late[G->vexsNum - 1] = early[G->vexsNum - 1];
	for (int i = G->vexsNum - 2; i >= 0;i--) {
		int min = Max;
		for (int j = 0; j < G->vexsNum; j++) {
			if (G->arcs[top[i]][j] != 0 && G->arcs[top[i]][j] < Max) {
				if (late[j] - G->arcs[top[i]][j] < min) {
					min = late[j] - G->arcs[top[i]][j];
				}
			}
		}
		late[top[i]] = min;
		printf("%d ", late[top[i]]);
	}
	printf("\n");

	for (int i = 0; i < G->vexsNum; i++) {
		if (early[i] == late[i]) {
			printf("%d ", i);
		}
	}
}

        运行的结果如下，第二行为事件的最早开始时间（拓扑排序正序），第三行为事件的最晚开始事件（拓扑排序倒序），最后一行为关键路径。

这就是文章的全部内容了，希望对你有所帮助，如有错误欢迎评论。