【基础】模拟题 数学处理类 日期

P8831 [传智杯 #3 练习赛] 儒略历

题目描述

在 1582 年之前，以 4 为倍数的年份为闰年。正常情况下，一年中一月到十二月的天数分别是 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 天。如果这年是闰年，那么二月则有 29 天。

但某位教皇发现这么做其实不够准确，会造成误差，因此规定从 1582 年开始，以 4 为倍数的年份，除了以 100 为倍数且不为 400 的倍数年份，才是闰年。同时为了消除误差，规定 1582 年 10 月 4 日的下一天是 1582 年 10 月 15 日，中间的日期就当作不存在了。

现在给出日期，计算这个日期到公元 1 年 1 月 1 日经过的天数。

输入格式

按照 日月年 的格式输入数据，其中日是 1 到 31 之间的整数，月是三个大写字母，年是 1 到 9999 之间的整数。保证这个日期是合法且存在的。

月份的大写字母：

• 1月：JAN
• 2月：FEB
• 3月：MAR
• 4月：APR
• 5月：MAY
• 6月：JUN
• 7月：JUL
• 8月：AUG
• 9月：SEP
• 10月：OCT
• 11月：NOV
• 12月：DEC

输出格式

输出一个整数表示答案

输入输出样例

输入 #1复制

1JAN1

输出 #1复制

0

输入 #2复制

4OCT1582

输出 #2复制

577736

输入 #3复制

15OCT1582

输出 #3复制

577737

输入 #4复制

21NOV2020

输出 #4复制

737751

调了半天终于对了（

---

Step 1: 读入

如题我们已知输入的格式是 日 月 年 ，而月是用字符串表示，所以我们需要把哪一月份给求出来。

根据题目给的缩写，我们就可以打表来计算月份。

string month[13]={"","JAN","FEB","MAR","APR","MAY","JUN","JUL","AUG","SEP","OCT","NOV","DEC"};

由于我们读入的是个字符串，所以我们紧接着还要把年和日求出来，先求日，再求年。

把字符串转化成数字这应该人人皆知如何处理，这里不做细讲。我们先把前面的数字给日，直到出现了字符，我们之后出现的数字才给年。

for(int i=0;i<st.size();i++){
	if(st[i]>='0'&&st[i]<='9'){
		if(!ok)d*=10,d+=int(st[i]-48ll);//在出现字符之前计算日。
		else y*=10,y+=int(st[i]-48ll);//在出现字符后计算年。
	}
	else mon+=st[i],ok=1;//ok 代表是否出现了字符，mon最终是月份的字符串。
}

别问我为什么是减去 48ll ,只是防止 ctjer。

把月份化成数字也就很方便了。

for(int i=1;i<=12;i++)
	if(mon==month[i]){//正好匹配到一样的月份，i 的值即为月份。
		m=i;
		break;
	}

---

Step 2: 计算天数

题目由此可以化简为：我们已知现在是 y 年 m 月 d 日，求离 1 年 1 月 1 日多少天。

显然的，y 年不一定过完了，m 月也不一定过完了，所以我们不能直接加到它们的值，而是要到它们的值 -1。

由题我们又可以把月份分成3种情况：

1. 年 <1582<1582，闰年只需判断是否能被 4 整除。
2. 年 =1582=1582，不是闰年，10 月少了 10 天。
3. 年 >1582>1582，闰年包括普通和世纪闰年。

---

普通闰年：能被 4 整除不能被 100 整除。

世纪闰年：能被 400 整除。

拓展芝士：闰秒将在2035年取消。

---

根据上述条件，我们也就可以得出代码啦。

代码如下：

#include<bits/stdc++.h>
using namespace std;
string month[13]={"","JAN","FEB","MAR","APR","MAY","JUN","JUL","AUG","SEP","OCT","NOV","DEC"};
int a[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};//每个月的天数
signed main()
{
	int d=0,m=0,y=0;
	string st,mon="";
	bool ok=0;
	cin>>st;
	for(int i=0;i<st.size();i++){
		if(st[i]>='0'&&st[i]<='9'){
			if(!ok)d*=10,d+=int(st[i]-48ll);//在出现字符之前计算日。
			else y*=10,y+=int(st[i]-48ll);//在出现字符之前计算年。
		}
		else mon+=st[i],ok=1;//ok 代表是否出现了字符，mon最终是月份的字符串。
	}
	for(int i=1;i<=12;i++)
		if(mon==month[i]){//正好匹配到一样的月份，i 的值即为月份。
			m=i;
			break;
		}
	//cout<<y<<' '<<m<<' '<<d<<'\n';
	if(y<1582)a[2]=(y%4==0?29:28);;//第一种情况。
	else if(y==1582)a[2]=28;;//第二种情况。
	else a[2]=(y%4==0&&y%100!=0||y%400==0?29:28);;//第三种情况。
	if(y==1582&&m>=10&&d>=15)d-=10;//如果正好在1582年的10月15号及以后，减去 10。
	while(m--)d+=a[m];//完整走完的月的总天数。
	while(y--&&y){//完整走完的年的总天数
		if(y<1582)d+=(y%4==0?366:365);//第一种情况。
		else if(y==1582)d+=355;//第二种情况。
		else d+=(y%4==0&&y%100!=0||y%400==0?366:365);//第三种情况。
	}
	cout<<d-1;//因为求的是与 1 年 1 月 1 日之间的天数，d 为天数，所以输出 d-1 。
}

P7075 [CSP-S2020] 儒略日

题目描述

为了简便计算，天文学家们使用儒略日（Julian day）来表达时间。所谓儒略日，其定义为从公元前 4713 年 1 月 1 日正午 12 点到此后某一时刻间所经过的天数，不满一天者用小数表达。若利用这一天文学历法，则每一个时刻都将被均匀的映射到数轴上，从而得以很方便的计算它们的差值。

现在，给定一个不含小数部分的儒略日，请你帮忙计算出该儒略日（一定是某一天的中午 12 点）所对应的公历日期。

我们现行的公历为格里高利历（Gregorian calendar），它是在公元 1582 年由教皇格里高利十三世在原有的儒略历（Julian calendar）的基础上修改得到的（注：儒略历与儒略日并无直接关系）。具体而言，现行的公历日期按照以下规则计算：

1. 公元 1582 年 10 月 15 日（含）以后：适用格里高利历，每年一月 31天、 二月 28 天或 29 天、三月 31 天、四月 30 天、五月 31 天、六月 30 天、七月 31 天、八月 31 天、九月 30 天、十月 31 天、十一月 30 天、十二月 31 天。其中，闰年的二月为 29 天，平年为 28 天。当年份是 400 的倍数，或日期年份是 4 的倍数但不是 100 的倍数时，该年为闰年。
2. 公元 1582 年 10 月 5 日（含）至 10 月 14 日（含）：不存在，这些日期被删除，该年 10 月 4 日之后为 10 月 15 日。
3. 公元 1582 年 10 月 4 日（含）以前：适用儒略历，每月天数与格里高利历相同，但只要年份是 44 的倍数就是闰年。
4. 尽管儒略历于公元前 45 年才开始实行，且初期经过若干次调整，但今天人类习惯于按照儒略历最终的规则反推一切 1582 年 10 月 4 日之前的时间。注意，公元零年并不存在，即公元前 1 年的下一年是公元 1 年。因此公元前 1 年、前 5 年、前 9 年、前 13 年……以此类推的年份应视为闰年。

输入格式

第一行一个整数 QQ，表示询问的组数。
接下来 QQ 行，每行一个非负整数 riri​，表示一个儒略日。

输出格式

对于每一个儒略日 riri​，输出一行表示日期的字符串 sisi​。共计 QQ 行。 sisi​ 的格式如下：

1. 若年份为公元后，输出格式为 Day Month Year。其中日（Day）、月（Month）、年（Year）均不含前导零，中间用一个空格隔开。例如：公元 2020 年 11 月 7 日正午 12 点，输出为 7 11 2020。
2. 若年份为公元前，输出格式为 Day Month Year BC。其中年（Year）输出该年份的数值，其余与公元后相同。例如：公元前 841 年 2 月 1 日正午 12 点，输出为 1 2 841 BC。

输入输出样例

输入 #1复制

3
10
100
1000

输出 #1复制

11 1 4713 BC
10 4 4713 BC
27 9 4711 BC

输入 #2复制

3
2000000
3000000
4000000

输出 #2复制

14 9 763
15 8 3501
12 7 6239

输入 #3复制

见附件中的 julian/julian3.in

输出 #3复制

见附件中的 julian/julian3.ans

说明/提示

【数据范围】

测试点编号	Q=	ri≤
11	1000	365
22	1000	104
33	1000	105
44	10000	3×1053×105
55	10000	2.5×1062.5×106
66	105	2.5×1062.5×106
77	105	5×1065×106
88	105	107107
99	105	109109
1010	105	年份答案不超过 10^9

在一种历法中，日期计算以400年为周期，每400年都有恰好146097天

预处理出400年内的情况，将年份模400即可快速得到答案

几个简化代码的技巧：

对于格里高利历，以1200年1月1日为起始日，rr减去跳过的天数（2159351）

判断历法：r⩽2299160r⩽2299160即为儒略历

公元前xx年视为1−x1−x年

#include<bits/stdc++.h>
typedef long long ll;
const int N=146097;//格里高利历400年的天数
int T,y[N],m[N],d[N];
ll n,t;
inline int md(int y,int m){//格里高利历y年m月的天数
    if(m==2)return y%4?28:y%100?29:y%400?28:29;
    return m==4||m==6||m==9||m==11?30:31;
}
int main(){
    m[0]=d[0]=1;
    for(int i=1;i<N;++i){
        d[i]=d[i-1]+1;m[i]=m[i-1];y[i]=y[i-1];
        if(d[i]>md(y[i],m[i]))++m[i],d[i]=1;
        if(m[i]>12)++y[i],m[i]=1;
    }//y[i],m[i],d[i]分别表示从0年1月1日经过i天的年月日
    scanf("%d",&T);
    while(T--){
        scanf("%lld",&n);
        if(n>2299160){//格里高利历
            n-=2159351;
            t=n/N*400+1200;
            n%=N;
        }else{
            t=n/1461*4-4712;//1461是儒略历4年的天数
            n%=1461;
        }
        if(t+y[n]>0)printf("%d %d %lld\n",d[n],m[n],t+y[n]);
        else printf("%d %d %lld BC\n",d[n],m[n],1-t-y[n]);
    }
}

1. 1010 分做法

由于第一个点 ri≤365ri​≤365 ，所以判断几月几日就好。

等等，好像没那么简单？

有的同学发现了一点：一月一日是第 00 天，那么第 365365 天不就到后一年去了吗？

其实公元前4713年是一个闰年，因为 4713≡1   (mod 4)4713≡1   (mod 4) ，而公元前1年为闰年。

所以只要枚举判断月份的前缀和是否超过了 riri​ 即可。

	month[2]++;
	int qwq=0,mth;
	for(int i=1;i<=12;i++){
		qwq+=month[i];
		if(qwq>=k){
			mth=i;
			k-=(qwq-month[i]);
			printf("%lld %lld 4713 BC\n",k,mth);
			break;
		}
	}
	month[2]--;

2. 4040 分做法

首先，公元1582年10月4日是第 22991602299160 天，所以只处理适用儒略历的就可以拿到 4040 分了。

那如何处理儒略历呢？

注意到，儒略历 44 年一循环，所以可以让 riri​ 对 365×4+1365×4+1 取余，求出大致年份，再一年一年判断在哪一年。

然后再向上面一样判断月、日就好了。

void count_date(int year,int k,int r){
	if(r==1)month[2]++;
	int qwq=0,mth;
	for(int i=1;i<=12;i++){
		qwq+=month[i];
		if(qwq>=k){
			mth=i;
			k-=(qwq-month[i]);
			if(year-4713<0)printf("%lld %lld %lld BC\n",k,mth,4713-year);
			else printf("%lld %lld %lld\n",k,mth,year-4712);
			break;
		}
	}
	if(r==1)month[2]--;
}

		scanf("%lld",&n);
			int k=n%(365*4+1),year=n/(365*4+1)*4,r=1;
			if(k>=366)k-=365,year++,r=0;
			if(k>=366)k-=365,year++;
			if(k>=366)k-=365,year++;
			if(r==1)k++;
			count_date(year,k,r);

3. 100100 分做法

没错，就是 100100 分做法。

首先，对于格里高利历，有个很没良心的地方：当年份是 400400 的倍数，或日期年份是 44 的倍数但不是 100100 的倍数时，该年为闰年。

所以，变成了 400400 一周期。怎么办？

其实和 4040 分做法一样处理就行了。

具体来说，就是把那几个if语句写个循环，道理是一样的。

注意，循环里还是要判断闰年。

还有，由于以公元1600年1月1日为原点写起来会比较舒服（周期起点），所以可以为了减少代码量，特判一下公元1582年和公元1600年之间的那几年。

下面是完整的代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
int q,n,rsum,month[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
void count_date(int year,int k,int r){
	if(r==1)month[2]++;
	int qwq=0,mth;
	for(int i=1;i<=12;i++){
		qwq+=month[i];
		if(qwq>=k){
			mth=i;
			k-=(qwq-month[i]);
			if(year-4713<0)printf("%lld %lld %lld BC\n",k,mth,4713-year);
			else printf("%lld %lld %lld\n",k,mth,year-4712);
			break;
		}
	}
	if(r==1)month[2]--;
}//儒略历时代的count_date
void count_date2(int year,int k,int r){
	if(r==1)month[2]++;
	int qwq=0,mth,f=0;
	for(int i=1;i<=12;i++){
		qwq+=month[i];
		if(qwq>=k){
			mth=i;
			k-=(qwq-month[i]);
			printf("%lld %lld %lld\n",k,mth,year+1600);
			f=1;
			break;
		}
	}
	if(f==0)printf("1 1 %lld\n",year+1601);
	if(r==1)month[2]--;
}//格里高利历时代的count_date
signed main(){
	//freopen("julian.in","r",stdin);
	//freopen("julian.out","w",stdout);
	for(int i=1;i<=400;i++)
		if((i%4==0&&i%100!=0)||i%400==0)rsum++;
	scanf("%lld",&q);
	while(q--){
		scanf("%lld",&n);
		if(n<=2299160){
			int k=n%(365*4+1),year=n/(365*4+1)*4,r=1;
			if(k>=366)k-=365,year++,r=0;
			if(k>=366)k-=365,year++;
			if(k>=366)k-=365,year++;
			if(r==1)k++;
			count_date(year,k,r);
		}//儒略历时代
		else {
			n+=10;//完美跳过不存在的那几天
			if(n<=2305457){
				int k=n%(365*4+1),year=n/(365*4+1)*4,r=1;
				if(k>=366)k-=365,year++,r=0;
				if(k>=366)k-=365,year++;
				if(k>=366)k-=365,year++;
				if(r==1)k++;
				count_date(year,k,r);
			}//特判的那几年
			else{
				n-=2305458;
				int k=n%(365*400+rsum),year=n/(365*400+rsum)*400,r=1;
				if(k>=366)k-=365,year++,r=0;
				for(int i=2;i<=399;i++){
					if(i%4==0&&i%100!=0){
						if(k>=367)k-=366,year++,r=1;
						else break;
					}
					else{
						if(k>=366)k-=365,year++,r=0;
						else break;
					}
				}
				if(r==1)k++;
				count_date2(year,k,r);
			}//格里高利历时代
		}
	}
	return 0;
}

时间复杂度：这看起来暴力的做法实际上是 O(q)O(q) 的不过常数比较大。

心血来潮，来一个 4040 分钟内想 + 写 + 调的做法，作为自己最后一篇题解吧。

这个做法有一个优点就是不会挂，只要过了大样例就是对的。

注意要 #define int long long !!!

首先将询问离线。

• 记录 rmon 数组表示闰年月份，mon 数组表示普通年月份。

• 定义一个结构体 QWQ 表示当前日期。

• 写一个判断闰年的函数 bool isr(QWQ x)。

• 写一个函数 QWQ nextday(QWQ x) 表示 xx 的下一天，返回一个 QWQ 类型。

这个函数需要讨论的是：当前是否是 15821582 年，当前是否是公元前 11 年（要进到公元 1 年），当前是否是 15821582 前的闰年，当前是否是 15821582 后的闰年。

这个分类讨论还是比较清晰的。

• 对于 −4713.1.1∼1999.12.31−4713.1.1∼1999.12.31 这段时间，从元年开始暴力 nextday 函数求。打表出来第 24515452451545 年就是 2000.1.12000.1.1。

接下来闰年很难做怎么办？继续考虑暴力。打表打出这 400400 年有 146097146097 天。

我们考虑暴力把这 400400 天用 nextday 函数跑出来，然后减去 24515452451545 再除 146097146097 求出这是第几轮循环（即第几个 400400 年），简单讨论一下就好了。

这样前面一步错样例就过不去，所以不可能挂分了。

时间复杂度 O(2451545+146097+Q)O(2451545+146097+Q)。我知道这样描述时间复杂度不严谨，但是就这样吧。

代码其实很好写，中间那一大段都是复制粘贴的，所以看起来很长，但实际就那么一点点...

#include<bits/stdc++.h>
#define ll long long
#define int long long //重要 
#define gc getchar
using namespace std;
inline ll read(){
    ll x=0,f=1;char ch=gc();
    while (!isdigit(ch)){if (ch=='-') f=-1;ch=gc();}
    while (isdigit(ch)){x=x*10ll+ch-'0';ch=gc();}
    return x*f;
}
const int mon[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
const int rmon[13]={0,31,29,31,30,31,30,31,31,30,31,30,31};
struct que{
    int t,id;
}q[1010101];
struct QWQ{
    int y,m,d;
}ori,tmp,ans[101010],X[300001];
int Q,mx,cnt; 
inline bool cmp(que a,que b){return a.t<b.t;}
inline int mabs(int x){return (x>0?x:-x);}
inline bool isr(QWQ a){
    if (a.y<0) return (-a.y-1)%4==0;
    if (a.y>=1582) return a.y%400==0||(a.y%4==0&&a.y%100);
    if (a.y%4==0) return 1;
    return 0;
}
inline QWQ nextday(QWQ a){ //分类讨论 
    QWQ ans=a;
    if (a.y==1582){
        if (a.m==12&&a.d==31) ans.y++,ans.d=1,ans.m=1;
        else if (a.m==10&&a.d==4) ans.d=15;
        else if (a.d==mon[a.m]) ans.d=1,ans.m++;
        else ans.d++;
        return ans;
    }
    if (a.y==-1&&a.m==12&&a.d==31) ans.y=1,ans.d=1,ans.m=1;    
    else if (isr(a)){
        if (a.m==12&&a.d==31) ans.y++,ans.d=1,ans.m=1;
        else if (a.d==rmon[a.m]) ans.d=1,ans.m++;
        else ans.d++;
    }else{
        if (a.m==12&&a.d==31) ans.y++,ans.d=1,ans.m=1;
        else if (a.d==mon[a.m]) ans.d=1,ans.m++;
        else ans.d++;
    }
    return ans;
}
signed main(){
    ori.y=-4713,ori.m=1,ori.d=1,cnt=-1;
    Q=read();
    for (int i=1;i<=Q;i++) q[i].id=i,q[i].t=read();
    sort(q+1,q+1+Q,cmp);
    tmp=ori;
    for (int i=1;i<=Q;i++){
        if (q[i].t>=2451545) break;
        mx=i; 
    }
    for (int i=1,now=0;i<=mx;i++){
        for (;now!=q[i].t;now++) tmp=nextday(tmp);
        ans[q[i].id]=tmp;
    }
    tmp.d=1,tmp.m=1,tmp.y=2000;
    for (;tmp.y!=2400;) X[++cnt]=tmp,tmp=nextday(tmp);
    for (int i=mx+1;i<=Q;i++){
        ans[q[i].id].d=X[(q[i].t-2451545)%146097].d;
        ans[q[i].id].m=X[(q[i].t-2451545)%146097].m;
        ans[q[i].id].y=X[(q[i].t-2451545)%146097].y+400*((q[i].t-2451545)/146097);
    }
    for (int i=1;i<=Q;i++){
        printf("%lld %lld %lld",ans[i].d,ans[i].m,mabs(ans[i].y));
        if (ans[i].y<0) printf(" BC");
        puts("");
    }
    return 0;
}

3254. Crontab

•    题目
•    提交记录
•    讨论
•    题解
•    视频讲解

Cron (源自希腊语 χρόνοςχρόνος，意思是时间〉是类 Unix 系统下基于时间的任务调度器，用于在固定的时间运行指定的任务(多为系统管理和维护的任务)。

Cron 适合于周期性重复调度的任务，通过crontab文件来描述调度任务的配置。

Crontab文件由若干行组成，每行是一条配置信息，格式如下:

<minutes> <hours> <day of month> <month> <day of week> <command>

表示在满足前 55 项所指定的时间来运行第 66 项 <command> 所描述的命令。

前 55 项用于描述时间，含义和取值范围如下:

• <minutes> 是分钟数，取值范围是 0−590−59;
• <hours> 是小时数，取值范围是 0−230−23;
• <day of month> 是月份中的天数，取值范围是 1−311−31;
• <month> 是月份，取值范围是 1−121−12，或 Jan - Dec ;
• <day of week> 是星期几，取值范围是 0−60−6，或 Sun - Sat。

对于前 55 项，除了可以直接给出数字或者英文缩写(不区分大小写)外，还可以出现星号 *(表示任何取值)、逗号 , (表示多个不同的取值)或减号 - (表示一段连续的取值范围)。

星号只能单独出现，减号和逗号可以配合出现。

Cron 每分钟检查一次系统时间，当系统时间同时满足这 55 项要求时，cron 将执行对应的命令。

给出一个时间段，以及一个 crontab 文件，请你编程输出在这段时间内的任务调度执行情况。

输入格式

输入第一行有 33 个整数 n、s、t𝑛、𝑠、𝑡，用空格分隔。n𝑛 表示接下来有 n𝑛 行，描述一个 crontab 文件。s𝑠 和 t𝑡 分别为系统运行的开始时间（包含）和结束时间（不包含)，格式为 yyyymmddHHMM(年、月、日、小时、分钟)。

接下来有 n𝑛 行，每行是一条 crontab 配置信息，相邻两项之间用一个空格分隔。

输出格式

输出有若干行，每行表示一个任务调度，由两部分构成︰第一部分是任务调度的时间，格式同样为 yyyymmddHHMM，第二部分是调度执行的命令。

两部分之间用一个空格分隔。

按照时间先后顺序输出。

如果同一时刻有多条命令满足调度条件，则按照输入给出的顺序输出。

数据范围

输入数据约定:

• 1≤n≤20,s≤t1≤𝑛≤20,𝑠≤𝑡
• 输入数据中给出的时间均在 1970-01-01 00:00 到 2099-12-31 23:59 之间。
• 输入中给出的命令只包含大小写字母、数字和下划线 _，不包含空格或其他符号。
• 保证输入中描述时间的部分都是合法的。对于减号描述的时间范围 x−y𝑥−𝑦，一定满足 x≤y𝑥≤𝑦。英文缩写的拼写保证是正确的。英文缩写和数值可以混合使用。分钟数和小时数可以有前导 00，也可以没有(例如，0000 和 00 都是合法的输入)，其他部分不会出现前导 00。
• 输入的每行不超过 100100 个字符。
• 保证输出内容不超过 1000010000 行。
• 提示:19701970 年 11 月 11 日是星期四。

输入数据特征(√√ 表示可以出现，×× 表示不会出现)∶

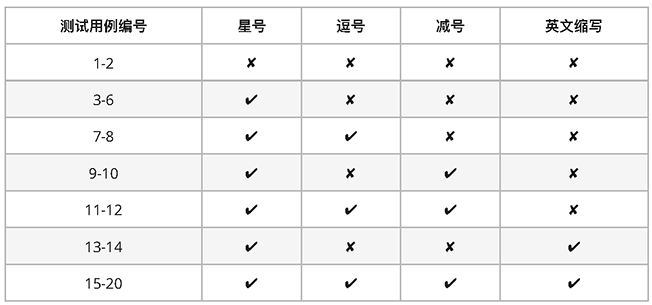
附：月份与星期的英文缩写对照表：

输入样例：

3 201711170032 201711222352
0 7 * * 1,3-5 get_up
30 23 * * Sat,Sun go_to_bed
15 12,18 * * * have_dinner

输出样例：

201711170700 get_up
201711171215 have_dinner
201711171815 have_dinner
201711181215 have_dinner
201711181815 have_dinner
201711182330 go_to_bed
201711191215 have_dinner
201711191815 have_dinner
201711192330 go_to_bed
201711200700 get_up
201711201215 have_dinner
201711201815 have_dinner
201711211215 have_dinner
201711211815 have_dinner
201711220700 get_up
201711221215 have_dinner
201711221815 have_dinner

样例解释

样例输入给出了 33 条 cron 配置信息，系统运行的开始时间是 2017-11-17 00:32(包含)，结束时间为 2017-11-22 23:52(不包含)。

每条配置信息的含义如下:
1．在星期一、三、四、五的 77 点整运行 get_up 命令。
2．在星期六、星期天的 2323 点 3030 分运行 go_to_bed 命令。
3．在每天的 1212 点 1515 分和 1818 点 1515 分运行 have_dinner 命令。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>

using namespace std;

int n;
int months[13] = {
    0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31
};

struct Timer
{
    int year, month, day, hour, minute, week;
    Timer(string str)
    {
        sscanf(str.c_str(), "%04d%02d%02d%02d%02d", &year, &month, &day, &hour, &minute);
    }
    bool operator< (const Timer& t) const
    {
        if (year != t.year) return year < t.year;
        if (month != t.month) return month < t.month;
        if (day != t.day) return day < t.day;
        if (hour != t.hour) return hour < t.hour;
        return minute < t.minute;
    }
    int is_leap()
    {
        if (year % 4 == 0 && year % 100 || year % 400 == 0)
            return 1;
        return 0;
    }
    int get_days()
    {
        if (month == 2) return months[2] + is_leap();
        return months[month];
    }
    void next()
    {
        if ( ++ minute == 60)
        {
            minute = 0;
            if ( ++ hour == 24)
            {
                hour = 0;
                week = (week + 1) % 7;
                if ( ++ day > get_days())
                {
                    day = 1;
                    if ( ++ month > 12)
                    {
                        month = 1;
                        year ++ ;
                    }
                }
            }
        }
    }
    string to_string()
    {
        char str[20];
        sprintf(str, "%04d%02d%02d%02d%02d", year, month, day, hour, minute);
        return str;
    }
};

struct Task
{
    bool minutes[60], hours[24], day_of_month[32], month[13], day_of_week[7];
    string name;
    bool check(Timer& t)
    {
        return minutes[t.minute] && hours[t.hour] && day_of_month[t.day] &&
            month[t.month] && day_of_week[t.week];
    }
}task[20];
unordered_map<string, int> nums;

void init()
{
    string keys[] = {
        "jan", "feb", "mar", "apr", "may", "jun",
        "jul", "aug", "sep", "oct", "nov", "dec",
        "sun", "mon", "tue", "wed", "thu", "fri",
        "sat"
    };
    int values[] = {
        1, 2, 3, 4, 5, 6,
        7, 8, 9, 10, 11, 12,
        0, 1, 2, 3, 4, 5,
        6
    };
    for (int i = 0; i < 19; i ++ )
        nums[keys[i]] = values[i];
}

int get(string str)
{
    if (str[0] >= '0' && str[0] <= '9') return stoi(str);
    string s;
    for (auto c: str) s += tolower(c);
    return nums[s];
}

void work(string str, bool st[], int len)
{
    if (str == "*")
    {
        for (int i = 0; i < len; i ++ ) st[i] = true;
    }
    else
    {
        for (int i = 0; i < str.size(); i ++ )
        {
            int j = i + 1;
            while (j < str.size() && str[j] != ',') j ++ ;
            string s = str.substr(i, j - i);
            i = j;
            int k = s.find('-');
            if (k != -1)
            {
                int l = get(s.substr(0, k)), r = get(s.substr(k + 1));
                for (int u = l; u <= r; u ++ ) st[u] = true;
            }
            else st[get(s)] = true;
        }
    }
}

int main()
{
    init();
    string start, end;
    cin >> n >> start >> end;
    for (int i = 0; i < n; i ++ )
    {
        string minutes, hours, day_of_month, month, day_of_week, name;
        cin >> minutes >> hours >> day_of_month >> month >> day_of_week >> name;
        work(minutes, task[i].minutes, 60);
        work(hours, task[i].hours, 24);
        work(day_of_month, task[i].day_of_month, 32);
        work(month, task[i].month, 13);
        work(day_of_week, task[i].day_of_week, 7);
        task[i].name = name;
    }

    Timer t("197001010000"), S(start), E(end);
    t.week = 4;

    int cnt = 0;
    while (t < E)
    {
        if (!(t < S))
        {
            for (int i = 0; i < n; i ++ )
                if (task[i].check(t))
                    cout << t.to_string() << ' ' << task[i].name << endl;
        }
        t.next();
    }

    return 0;
}