C语言：汉诺塔问题-CSDN博客

本文链接：https://blog.csdn.net/2302_80932177/article/details/138373426

汉诺塔的玩法是将一个木桩上的圆盘转移到另外一个木桩。移动规则：1、一次只能移动一个圆盘；2、每个桩上只有最顶层的圆盘可以移动，并且所移动的圆盘只能移到空木桩上或者它要比木桩顶层已存在的圆盘小。也就是说，您不能将大圆盘置于小圆盘之上。

一.问题分析

汉罗塔只能大圆盘在小圆盘的下面，并且一次只能移动一个圆盘。现有三个木桩，分别是A木桩,B木桩,C木桩,若要把A木桩上的所有圆盘都移到C木桩上，我们肯定要借助B木桩来实现的。所以我们假设A木桩为开始木桩，B木桩为中转木桩，则C木桩为目标木桩。(注意在实现的过程中，中转和目标是变化的，这里只是从最大方面来说)
若只有一个圆盘，则只需要移动一次即可，即A–>C
在这里插入图片描述
若有两个圆盘，则需要移动三次，即A–>B,A–>C,B–>C

若有三个圆盘，则需要移动7次，即A–>C,A–>B,C–>B,A–>C,B–>A,B–>C,A–>C

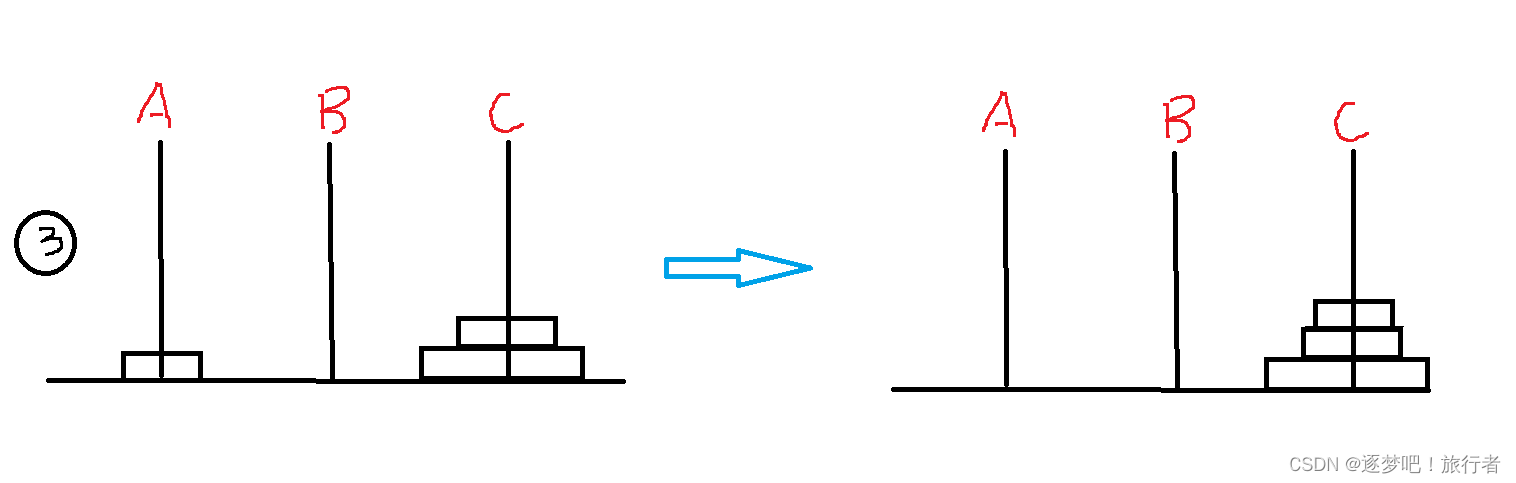
根据以上所举的例子，我们可以发现当有n个圆盘时，需要移动2^n-1次（2的n次方-1），由此可推得，当有4个圆盘时，需要移动15次。

二.代码实现

1.对于移动的如何移动（移动的路径），我们可以自定义一个move函数，无返回值，因为移动只能从一个木桩一道另一个木桩，所以需要有一个代表开始的参数，一个代表目标的参数，这个函数是用来打印移动路径的。
2.对于汉诺塔问题，我们一般都采用递归算法来解决，为什么呢？对于n个圆盘，我们可以把底部上面的n-1个圆盘看成一个只有n-1个圆盘的单独的汉诺塔问题，同理我们也可以把底部上面的n-2个圆盘看成一个只有n-2个圆盘的单独的汉诺塔问题，以此内推，就转换成了大问题化小问题的递归问题。这里我们自定义一个Hanluio函数，无返回值，有四个参数，一个参数代表有n个圆盘，一个是代表A木桩，一个代表B木桩，还有一个代表木桩。
在这里插入图片描述
接下来我们来看代码：

void move(char op1, char op2)
{
	printf("%c-->%c ", op1, op2);//代表从op1移到op2
}
void Hanluio(int n, char op1, char op2, char op3)//op1接收A，op2接收B,op3接收C
{
	if (n == 1)//只有一个圆盘，只需要一次就移动到目标木桩
	{
		move(op1, op3);
	}
	else
	{
		Hanluio(n - 1, op1, op3, op2);//这里代表A为开始，B为目标，C为中转
		move(op1, op3);//代表从op1移到op3
		Hanluio(n - 1, op2, op1, op3);//这里代表A为中转，B为开始，C为目标
	}
}
int main()
{
	Hanluio(1, 'A', 'B', 'C');
	printf("\n");
	Hanluio(2, 'A', 'B', 'C');
	printf("\n");
	Hanluio(3, 'A', 'B', 'C');
	return 0;
}