前言
本文主要是发现有很多🤷♀️(新手小白)没有办法很清楚的理解二进制原码,反码和补码之间的关系😣以及计算机内部到底是怎么用补码进行运算的进行一个详细的解释😏写下这篇🐷(小猪)都能看懂的三码介绍(●’◡’●)
原码,反码,补码的故事(个人瞎编版)
为了让读者更好的理解,我就用我自己的语言瞎编😁一些东西,纯属虚构别当真,这里我们管原码叫小原,反码叫反骨仔,补码叫小猪(🐷)。
小原(原码)
有一天小原同学设计了一款计算机,他打算用自己的名字命名,于是就叫小原计算机╰(°▽°)╯,小原打算用他的计算机做数学题,小原决定用八位二进制数最高位为零作为正数,最高位为1的八位二进制数为负数例如:
1 0 D = 0 000101 0 B − 1 0 D = 1 000101 0 B 10_D = 0 \ 0001010_B \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -10_D = 1 \ 0001010_B 10D=0 0001010B −10D=1 0001010B
首位(最高位)小原决定命名为符号位剩余的都叫数值位,这便是小原的数值计算器,小原觉得自己特别聪明(❁´◡`❁)【我简直是天才😏】他可以算 1 1111111~0 1111111之间的数字了(-127 ~ 127)
小原用他的计算机进行计算:
0 0001010 + 0 0001010 = 0 0010100 \ \ \ \ 0\ 0001010 \\+\ 0\ 0001010\\=0\ 0010100 0 0001010+ 0 0001010=0 0010100
简直是完美一点也没问题,那我们再算一个 -2+2吧
1 0000010 + 0 0000010 = 1 0000100 \ \ \ \ 1\ 0000010 \\ +\ 0 \ 0000010 \\ = 1\ 0000100 1 0000010+ 0 0000010=1 0000100
偶买噶得😣,为什么变成-4了呀,我好像设计的有问题,这不对要是要计算我得额外规定符号数,±分别让计算机识别,我的加减运算复杂,还需判断符号和绝对值,而且1 0000000 和 0 0000000到底哪个才算是鸭蛋呢???
why baby why tall me why? 小原顿感道心破碎,我的计算机是废物呜呜呜~
此时此刻小原belike:
反骨仔(反码)
反骨仔看见小原就说看我的,你的正数我都不碰,你的负数我就是要跟你反着来,我刚你全部变成反的肯定就是对的,就是要气死你😏
看我算:(-2+2)
1 1111101 + 0 0000010 = 1 1111111 \ \ \ \ 1\ 1111101 \\ +\ 0 \ 0000010 \\ = 1\ 1111111 1 1111101+ 0 0000010=1 1111111
我把答案的数值位也全反过来,我就是要跟你反着来,我得到了 1 0000000,我的答案是对的,我的计算机比你小原的厉害🤷♀️小原说:那你的0 0000000 也是零吗?反骨仔也很疑惑怎么会这样我已经用循环的方式让数可以正常计算了呀,但是好像依旧没有解决两个零的问题呀,要是计算下去我就得格外规定这个零导致我的溢出判断依旧复杂。
>经过一整子深思熟虑以后,他决定求助聪明的小猪。
小猪🐷(补码)
小猪看了以后说给我一个钟,我用钟告诉你们,小原的正数我也不动,但是反骨仔(反码)你的反过来我要末尾+1,这是为了区分+0 和 -0 同时也为了简化溢出的判断这样不用循环进位,比如对于一个n位的进制位来说,小原(原码)的方式都不能方便的进行运算,对于负数 -x 反骨仔(反码)是(2^n - 1)-x 我(补码)就是2 ^n - x 这样有什么好处呢,这样可以完全用加法取代减法😏不会出现+0,-0的歧义,还可以通过简单的符号位进位来判断溢出,我们把 0 0000000——>(0)0 1111111——>(127) 让 1 0000000——>(-128) 1 1111111——>(-1) 这样可以计算范围就有-128~127,像下面这张图一样😊😘
你们想想时钟是怎么转的呀时钟转一圈是12个小时,是不是从12转到12又重新从12开始了,那我们也这样,符号位只要进位了就舍弃,像钟表一样, ( x + 2 n ) m o d 2 n = x (x+2^n)\ mod\ 2^n = x (x+2n) mod 2n=x我们不看商,只看余数,利用模的思想25/12 = 2···1 那就等于1点,明白了吗?
我们拿补码来算几个数字。
4+(-5)
0 0000100 + 1 1111011 = 1 1111111 \ \ \ \ 0\ 0000100\\ \ +1\ 1111011\\ =1\ 1111111 0 0000100 +1 1111011=1 1111111
这个补码对应的刚好是-1,对补码再求补码会等于原码这里你可能会有疑问后面我会细细道来😘
1 1111111 − > 数值位取反( 1 0000000 )— > 加一( 1 0000001 ) 1 \ 1111111-> 数值位取反(1 \ 0000000)—>加一(1\ 0000001) 1 1111111−>数值位取反(1 0000000)—>加一(1 0000001)
知识小结
在上面的故事我们有一个原码反码补码的发展过程,原码没有办法简单进行正负相加的计算(需要格外规定加减符号)判断溢出麻烦,反码区分+0,-0要额外计算效率比较低,判断溢出麻烦补码将+0,-0统一用mod(模)的方式将减法变成加法,大大提高了运算效率
对于溢出只看操作数与结果的符号(第一种方法特别推荐):
正 + 正 → 结果为负 ⇒ 溢出
负 + 负 → 结果为正 ⇒ 溢出
异号相加 ⇒ 永远不会溢出
另外的方法:(不推荐)
Cn:最高数值位(第 n-1 位)向符号位(第 n 位)的进位
Cn+1:符号位向更高位(第 n+1 位,即“溢出位”)的进位
溢出标志 V = Cn ⊕ Cn+1
V = 1 → 溢出
V = 0 → 无溢出
4 位例子
0111 (+7)
0101 (+5)
1100 (–4) ← 正+正=负,明显溢出
Cn = 1, Cn+1 = 0 → V = 1⊕0 = 1 ✔
一句话就是:符号位进位异或,不同就溢出;同号相加变号,也溢出
三个码之间的变换方式😏
原码变反码
正数:正数的原码反码补码一致
负数:符号位不变,数值位取反举例(-5)
1 0000101 (原码) ( 取反 ) 1 1111010 (反码) 1\ 0000101(原码)\\(取反)\\ 1\ 1111010(反码) 1 0000101(原码)(取反)1 1111010(反码)
反码变补码
正数:正数的原码反码补码一致
负数:反码末位加一
1 1111010 (反码) ( 加一 ) 1 1111011 (补码) 1\ 1111010(反码)\\(加一)\\ 1\ 1111011(补码) 1 1111010(反码)(加一)1 1111011(补码)
补码变原码
正数:正数的原码反码补码一致
负数:对补码再求补码
1 1111011 (原来的补码) ( 取反 ) 1 0000100 (补码的反码) ( 加一 ) 1 0000101 ( 原码 ) 1\ 1111011(原来的补码)\\(取反)\\ 1\ 0000100(补码的反码)\\(加一)\\ 1\ 0000101(原码) 1 1111011(原来的补码)(取反)1 0000100(补码的反码)(加一)1 0000101(原码)
是不是很神奇😍
补码的补码为什么是原码
很多小白听到补码的补码是原码的时候总是会想凭什么啊,怎么这么奇怪呢,其实一点也不奇怪,负数的补码是反码加一,是原码数值为取反加一,正数的原码反码补码是一样的我们不讨论。
(❁´◡`❁)我们知道补码是原码数值位取反加一,那么我们把他分成两部分,一部分是因为加一产生了变化的部分,一部分是没有产生变化的部分。
拿-5举例
− 5 = 1 0000101 ( 原码) − 5 = 1 1111011 ( 补码 ) \ \ -5=1\ 0000101(原码)\\-5 = 1\ 1111011(补码) −5=1 0000101(原码)−5=1 1111011(补码)
这里最末尾的1是因为加一发生变化了的,他跟原码是一致的,没产生变化的是跟原码相反的,那么补码既然是这样的话,我再对他取反加一的话,是不是说因为加一产生变化的部位还是与原码一致,没发生变化的部分与原码是相反的呢,答案确实是这样的。
− 5 = 1 0000101 ( 原码) − 5 = 1 1111011 ( 补码 ) 补码的反码 − 5 = 1 0000100 ( 反码 ) 对补码取反后可以很清楚的看见除了因为加一变化的部位,补码取反码后都跟原码一致了。 补码的补码 − 5 = 1 0000101 ( 补码 ) 很清楚的看见,补码的补码跟原码是一致的。 \ \ -5=1\ 0000101(原码)\\-5 = 1\ 1111011(补码)\\补码的反码\\ -5 = 1\ 0000100(反码)\\对补码取反后可以很清楚的看见除了因为加一变化的部位,补码取反码后都跟原码一致了。\\补码的补码\\-5 = 1\ 0000101(补码) \\很清楚的看见,补码的补码跟原码是一致的。 −5=1 0000101(原码)−5=1 1111011(补码)补码的反码−5=1 0000100(反码)对补码取反后可以很清楚的看见除了因为加一变化的部位,补码取反码后都跟原码一致了。补码的补码−5=1 0000101(补码)很清楚的看见,补码的补码跟原码是一致的。
我们可以多看几个数加深我们的理解
-10
− 10 = 1 0001010 补码 − 10 = 1 1110110 可以看到后面两个数跟原码是一致的,其他(除符号位)是相反的 补码的反码 − 10 = 1 0001001 可以看到除了后面因为加一产生变化的数其他位已经与原码相同了 补码的补码(原码) − 10 = 1 0001010 加一以后已经是一模一样了。 -10 = 1\ 0001010\\补码\\-10 = 1\ 1110110\\可以看到后面两个数跟原码是一致的,其他(除符号位)是相反的\\补码的反码\\-10 = 1\ 0001001\\可以看到除了后面因为加一产生变化的数其他位已经与原码相同了\\补码的补码(原码)\\-10 = 1\ 0001010\\加一以后已经是一模一样了。 −10=1 0001010补码−10=1 1110110可以看到后面两个数跟原码是一致的,其他(除符号位)是相反的补码的反码−10=1 0001001可以看到除了后面因为加一产生变化的数其他位已经与原码相同了补码的补码(原码)−10=1 0001010加一以后已经是一模一样了。
-11
− 11 = 1 0001011 (开始的原码) − 11 = 1 1110101 (开始的补码) − 11 = 1 0001010 (补码的反码) − 11 = 1 0001011 (补码的补码) -11 = 1\ 0001011(开始的原码)\\-11 = 1\ 1110101(开始的补码)\\-11 = 1\ 0001010(补码的反码)\\-11 = 1\ 0001011(补码的补码) −11=1 0001011(开始的原码)−11=1 1110101(开始的补码)−11=1 0001010(补码的反码)−11=1 0001011(补码的补码)
我相信你已经特别明白了但是我还是不放心,就说明一下它的数学原理(上面是我瞎编的,但它很对,特别对,相当的对😊)
数学原理:mod的意思是只取余数部分
对于一个 n 位数,补码表示的范围是 : − 2 ( n − 1 ) 到 2 ( n − 1 ) − 1 一个数 x 的补码可以表示成( 2 n + x ) m o d ( 2 n ) 对补码再次求补码 2 n + ( 2 n + x ) m o d ( 2 n ) = ( 2 ∗ 2 n + x ) m o d 2 n = x m o d ( 2 n ) 就是原码。 对于一个n位数,补码表示的范围是:\ \ \ \ \ -2^{(n-1)}到2^{(n-1)}-1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\一个数x的补码可以表示成(2^{n}+x)mod\ (2^n)对补码再次求补码\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\2^{n}+(2^{n}+x)\ mod\ (2^n)=(2*2^n+x)\ mod\ 2^n =x\ mod\ ( 2^n)就是原码 。\ \ \ \ \ \ \ \ 对于一个n位数,补码表示的范围是: −2(n−1)到2(n−1)−1 一个数x的补码可以表示成(2n+x)mod (2n)对补码再次求补码 2n+(2n+x) mod (2n)=(2∗2n+x) mod 2n=x mod (2n)就是原码。
结语
这次的结语包括了我整篇文章的创作过程,还有一些留给读者的话,由于需要详细,我希望我做出这篇文章是那种能让人看一遍就对原码,反码,补码有一个比较完整清晰的了解,所以也是花了不少心思,制作时间可能比较长。
创作过程
2025.9.3 21 : 32 完成故事编写, 23 : 50 进行第一次阅读修正和补充 2025.9.9 22 : 00 前段时间数学建模去了,我要先看两遍文章 写了一点【 23 : 19 】好累好累我要去休息了 2025 : 9 : 12 1 : 19 明天看一眼差不多就发了 2025.9.3\\21:32完成故事编写,23:50进行第一次阅读修正和补充\\ 2025.9.9\\22:00前段时间数学建模去了,我要先看两遍文章\\写了一点【23:19】好累好累我要去休息了 \\2025:9:12\ \ \ \ 1:19明天看一眼差不多就发了 2025.9.321:32完成故事编写,23:50进行第一次阅读修正和补充2025.9.922:00前段时间数学建模去了,我要先看两遍文章写了一点【23:19】好累好累我要去休息了2025:9:12 1:19明天看一眼差不多就发了
给读者的话
整篇文章是我用自己学习上的经验进行的总结,用我认为好理解的方式把知识简化写出来,上面的故事可能不是特别好,但是也能看出原码反码补码的一个大致的发展过程,如果文章有什么问题请给我留言,我会进行更正修改,要是这篇文章没有让你一眼看懂,那多半是我学习功底的问题,后期我会不定期的进行修正补足,争取做出一篇谁都能看懂的文章。






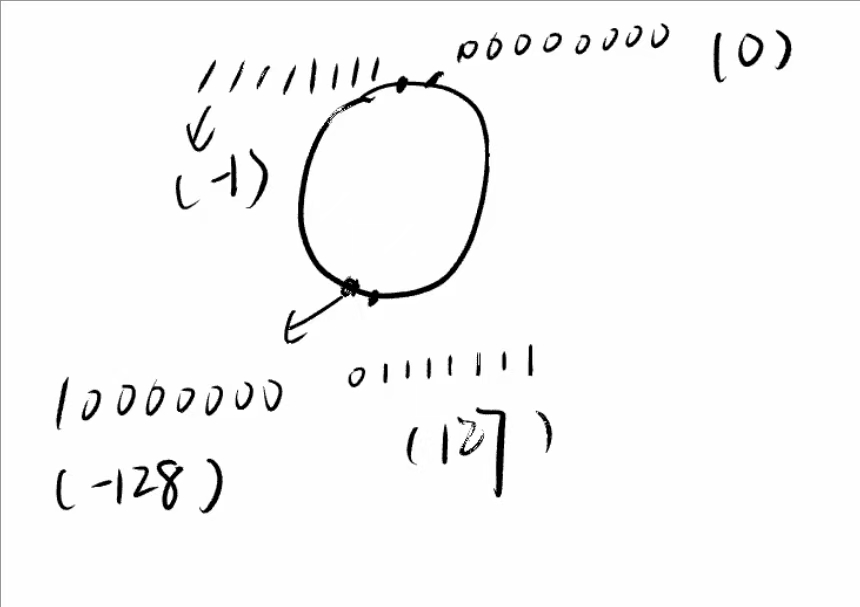


















 5928
5928


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?







