C++个人算法模版总结

清心悬玉

已于 2024-05-27 21:33:49 修改

阅读量692

点赞数 22

文章标签：算法 c++ 数据结构经验分享学习

于 2024-05-24 22:03:30 首次发布

本文链接：https://blog.csdn.net/2303_76151267/article/details/138865503

版权

文章目录

一、基础算法
二、数据结构
三、图论
四、数学知识
五、提高

一、基础算法

1. 归并排序

应用：超快速排序、求逆序对数量、相邻两两交换
n ( log₂n )

int merge_sort(int l,int r)
{
    if(l>=r) return 0;
    int mid=l+r>>1;
    int res=merge_sort(l,mid)+merge_sort(mid+1,r);
    int k=0,i=l,j=mid+1;
    while(i<=mid&&j<=r)
        if(a[i]<=a[j]) tmp[k++]=a[i++];
        else tmp[k++]=a[j++],res+=mid-i+1;
    while(i<=mid) tmp[k++]=a[i++];
    while(j<=r) tmp[k++]=a[j++];
    for(int j=0,i=l;i<=r;i++,j++) a[i]=tmp[j];
    return res;
}
int main()
{
        cin>>n;
        for(int i=0;i<n;i++) cin>>a[i];
        cout<<merge_sort(0,n-1)<<endl;
}

2. 二分

整数二分
log₂n

	// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用
	int l=?,r=?;
	while(l<r)
	{
		int mid=l+r>>1;
		if(check(mid)) r=mid;
		else l=mid+1;
	}
	cout<<l;
	
	// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用
	int l=?,r=?;
	while(l<r)
	{
		int mid=l+r+1>>1;
		if(check(mid)) l=mid;
		else r=mid-1;
	}
	cout<<l;

计算三次方根

	x=cbrt(8);
	//x=2.0 (double类型)

3. 高精度

加法

#include <iostream>
#include <vector>
using namespace std;

const int N = 1e6 + 10;

// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{
    if (A.size() < B.size()) return add(B, A);

    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++ )
    {
        t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }

    if (t) C.push_back(t);
    return C;
}

int main()
{
	string a, b;
	vector<int> A, B;
	
	cin >> a >> b;
	
	for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
	for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
	
	auto C = add(A, B);
	for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
	return 0;
}

减法

#include <iostream>
#include <string>
#include <vector>
using namespace std;

// 返回A >= B是否成立
bool cmp(vector<int>& A, vector<int>& B)
{
    if (A.size() != B.size()) return A.size() >= B.size();
    
    for (int i = A.size() - 1; i >= 0; i--) 
        if (A[i] != B[i])
            return A[i] >= B[i];

    return true;
}
// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ )
    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main()
{
    string a, b;
    vector<int> A, B;

    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');

    vector<int> C;
    if (cmp(A, B))
	{
        C = sub(A, B);
    }
	else
	{
        C = sub(B, A);
        printf("-");
    }

    for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);

    return 0;
}

乘法

string乘以int(等)

#include <iostream>
#include <vector>

using namespace std;

// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;
    
    for(int i = 0, t = 0; i<A.size() || t; i++)
    {
        if(i<A.size()) t += A[i] * b;
        C.push_back(t % 10);//取对10的余数存入
        t /= 10;//进位
    }//计算A * b
    
    while(C.size() > 1 && C.back() == 0) C.pop_back();//清除前导0
    
    return C;
}

int main()
{
    string a;
    int b;
    
    cin >> a >> b;
    
    vector<int> A;
    for (int i = a.size() - 1; i>=0; i--) A.push_back(a[i] - '0');
    
    auto C = mul(A, b);
    
    for (int i = C.size() - 1; i>=0; i--) cout << C[i];
    
    return 0;
}

除法

string乘以int(等)

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;

// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main()
{
    string a;
    int b;

    cin >> a >> b;
    
    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i--)  A.push_back(a[i] - '0');

    int r;
    
	auto C = div(A, b, r);
    
    for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    cout << endl;
    
	cout << r << endl;

    return 0;
}

4. 二维差分

使用二维前缀和求和

	//给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
	S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

5. 离散化

vector<int> v; // 存储所有待离散化的值

sort(v.begin(), v.end()); // 将所有值排序
v.erase(unique(v.begin(), v.end()), v.end());   // 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置，如果 v 中没有比 x 小的元素，则返回 n;
{
    int l = 0, r = v.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (v[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // 映射到1, 2, ...n
}

6. 区间合并

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

typedef pair<int, int> PII;

int n, l, r;
vector<PII> segs;

void merge(vector<PII> &segs)
{
    vector<PII> res;
    
    sort(segs.begin(), segs.end());//按区间左端点排序，sort默认排序segs的第一项
    
    int st = -2e9, ed = -2e9;//此时st和ed只要比-1e9小就可以
    for (auto seg : segs)
    {
        if (ed < seg.first)
        {
            if (st != -2e9) res.push_back({st, ed});
            st = seg.first;
            ed = seg.second;
        }
        else ed = max(ed, seg.second);
    }
    
    if (st != -2e9) res.push_back({st, ed});
    
    segs = res;//不能忘
}

int main()
{
    cin >> n;
    
    for (int i = 0; i < n; i ++ )
    {
        cin >> l >> r;
        segs.push_back({l, r});
    }
    
    merge(segs);
    
    cout << segs.size() << endl;
    
    return 0;
}//该代码引用AcWing网站的代码

二、数据结构

7. 双链表

	// e[]表示节点的值，l[]表示节点的左指针，r[]表示节点的右指针，idx表示当前用到了哪个节点
	int e[N], l[N], r[N], idx;
	
	// 初始化
	void init()
	{
	    //0是左端点，1是右端点
	    r[0] = 1, l[1] = 0;
	    idx = 2;
	}
	
	// 在节点a的右边插入一个数x
	void insert(int a, int x)
	{
	    e[idx] = x;
	    l[idx] = a, r[idx] = r[a];
	    l[r[a]] = idx, r[a] = idx ++ ;
	}
	
	// 删除节点a
	void remove(int a)
	{
	    l[r[a]] = l[a];
	    r[l[a]] = r[a];
	}

8. 滑动窗口

#include <iostream>
using namespace std;

const int N = 1e6 + 10;

int q[N], a[N], hh, tt = -1;
int n, k;

int main()
{
   scanf("%d%d", &n, &k);
   for (int i = 0; i < n; i++) scanf("%d", &a[i]);
   
   // i 本质是窗口的依次经历的右端点
   for (int i = 0; i < n; i++)
   {
       // 当前窗口区间是[i - k + 1, i]
       if (hh <= tt && q[hh] < i - k + 1) hh++; 
       while (hh <= tt && a[q[tt]] >= a[i]) tt--;
       q[++tt] = i;
       
       if (i + 1 >= k) printf("%d ", a[q[hh]]);
   }//求区间最小
   puts("");
   
   hh = 0, tt = -1;
   for (int i = 0; i < n; i++)
   {
       if (hh <= tt && q[hh] < i - k + 1) hh++;
       while (hh <= tt && a[q[tt]] <= a[i]) tt--;
       q[++tt] = i;
       
       if (i + 1 >= k) printf("%d ", a[q[hh]]);
   }//求区间最大
    
    return 0;
}

9. KMP

    // s[]是长文本，p[]是模式串，n是s的长度，m是p的长度
	// 求模式串的Next数组：
	// get_next()
	for (int i = 2, j = 0; i <= m; i ++ )
	{
	    while (j && p[i] != p[j + 1]) j = ne[j];
	    if (p[i] == p[j + 1]) j ++ ;
	    ne[i] = j;
	}
	
	// 匹配
	for (int i = 1, j = 0; i <= n; i ++ )
	{
	    while (j && s[i] != p[j + 1]) j = ne[j];
	    if (s[i] == p[j + 1]) j ++ ;
	    if (j == m)
	    {
	    	//匹配完成后的具体操作
            //如：输出以0开始的匹配子串的首字母下标
            //l 
            cout<<i-m<<' ';//若从1开始，加1
            //r：l+m-1即可 
	        j = ne[j];
	    }
	}

10. 并查集

(1)朴素并查集：

    int p[N]; //存储每个点的祖宗节点

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);


(2)维护size的并查集：

    int p[N], size[N];
    //p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        size[i] = 1;
    }

    // 合并a和b所在的两个集合：
    size[find(b)] += size[find(a)];
    p[find(a)] = find(b);


(3)维护到祖宗节点距离的并查集：

    int p[N], d[N];
    //p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x)
        {
            int u = find(p[x]);
            d[x] += d[p[x]];
            p[x] = u;
        }
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        d[i] = 0;
    }

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);
    d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量

11. 哈希

    typedef unsigned long long ULL;
	ULL h[N], p[N], P=131(或13331); // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
	
	// 初始化
	p[0] = 1;
	for (int i = 1; i <= n; i ++ )
	{
	    h[i] = h[i - 1] * P + str[i];
	    p[i] = p[i - 1] * P;
	}
	
	// 计算子串 str[l ~ r] 的哈希值
	ULL get(int l, int r)
	{
	    return h[r] - h[l - 1] * p[r - l + 1];
	}

12. STL

（1）Lambda函数（内置函数）

	int arr[5] = {3, 4, 2, 1, 7};
	sort(arr, arr + 5, [] (int a, int b) {
	    return a > b; //从大到小排序
	});

	auto func = [&, a, c](int x, int &y)->int {//不修改x，修改y
        b = 5, x = 6, y = 7;
        return a + b + c + x + y;
    };

	auto dfs = [&](auto&& self, int x) -> int{ // 一定要写返回值
   		return x > 0 ? x + self(self, x - 1) : 0;
	};
	printf("%d\n", dfs(dfs, 10));// 输出:55

（2）vector

2.1> 基础声明方式

	// 直接声明元素类型为int的vector
    vector<int> v1;

    // 利用构造函数声明一个长度为5的vector，
    vector<int> v2(5);
	
	// 利用构造函数声明一个长度为5，所有值为1的vector
    vector<int> v3(5, 1);
	
	// 另一种声明方式
    vector<int> v4 = {4, 5, 6, 7};

	// 也可以这样
    int b[4] = {1, 2, 3, 4};
    vector<int> v5(b + 1, b + 4); // v5元素为 2， 3， 4

2.2> 函数

	vector<int>v;
	
	v.push_back();
	v.pop_back();
	v.size();
	v.clear();//O(1)
	v.empty();//是否为空
	v.erase();//O(n)
		v.erase(v.begin()+1,v.begin()+4);//删除[1,4)，即区间[1,3] (数组下标)
	v.insert();//O(n)
		v.insert(v.begin()+1,5)//从前往后数，第一个元素后面插入5
		v.insert(v.begin()+2,2,6); // 往第2个元素后面插入2个6
		v.insert(v.begin() + 3, b + 1, b + 3); // 往第3个元素后面插入数组b中下标从1~2的数
	v.resize();//O(n)
		v.resize(10); // 重置v的大小为10，其值为前10个元素，不够补0
		v.resize(10, 2); // 重置v大小为10，其值为前10个元素，不够补2;
		
	vector<int>a,b;
	a.swap(b);//交换a,b两个vector
	
	begin返回vector起始的迭代器，end是vector最后一个元素的下一个位置的迭代器
	vector<int> v = {4, 5, 6, 7};
	cout<< *v.begin() <<endl;//输出4
	cout<< *(v.end()-1) <<endl;//输出7

（3）string

3.1> 基础声明方式

	// 方式一
	string s1;
	
	// 方式二
	string s2 = "123";
	
	// 方式三，初始化为由3个c组成的字符串
	string s3(3, 'c');
	
	// 方式四 相当于方式二
	string s4("123");
	
	// 方式五，和方式四是等价的
	char chr[] = "abc";
	string s5(chr);

3.2> 函数

	类似vector的函数
	s.push_back();
	s.pop_back();
	s.size(), s.length();
	s.clear();
	s.empty();
	begin(), end();
	+, +=//在时间复杂度上相差较大，如：O(n)与O(1)
	swap();
	resize();
	s.front();
	s.back();

	find();//O(n)
		s.find('c')//从0开始找字符c
		s.find("cd",3)//从下标3开始找字符串cd,返回c的下标
		找不到则返回string::npos//常量
	
	substr();//O(n)
		s.substr(3)//3~结束
		s.substr(3,3)//[3,3+3)，从3开始长度为3的字符串
	
	replace();//O(1)
		s.replace(3,2,"123456")//从3开始长度为2的字符创替换为"123456"
		s.replace(3,2,"123456",2,2)//从3开始长度为2的字符创替换为"34"
		s.replace(3,2,5,'#')//从3开始长度为2的字符创替换为"#####"
	
	s.append();
		添加字符串类型
		x="123456";
		s.append(x,2,2);//尾部加上"34"
	
	compare();
		a.compare(b)<0 //a<b
		a.compare(2,1,b,3,2)<0 //a[2,2]<b[3,4] (字典序)
	
	insert();//O(n)
		a.insert(2,b)//从前往后数第2个元素后面插入字符串b
		a.insert(2,b,3,2)//上述位置插入b[3,4]
	
	erase();
		s.erase(3)//删除下标3~n的字符串
		s.erase(3,1)//删除下标[3,3+1)，即[3,3]的字符串
	
	c_str();//将字符串转换成char*类型的字符串
	to_string();//可传入的参数有int、long long、double等
	stoi();//string->int
		与其类似的还有stol、stof、stod、stoll、stold、stoull等，
		分别对应返回值为long、double、long long、long double、unsigned long long
	getline(cin, s)//读入整行string，前面有换行符需要先getchar()
	
	sstream();//缺点：速度慢，优点：大模拟省事
		#include <sstream> // 需要导入此头文件
	    string str = "what are you doing now", sub;
	    stringstream ss1(str); // 将流初始化
	    while (ss1 >> sub) { // 想流一样读入到sub里面
	        cout << sub << endl;
	    }
	    /*
	    输出结果
	    what
	    are
	    you
	    doing
	    now
	    */
	
	    str = "123 45.6";
	    stringstream ss2;
	    ss2 << str; // 像流一样读入到ss2
	    int x;
	    double y;
	    ss2 >> x >> y; // 像流一样读入到 x 和 y 里面
	    cout << x << ' ' << y; // 123 45.6

（4）stack

先进后出
无clear

	stack<int>stk;
	size();
	push();
	pop();//弹出栈顶元素，如果此时栈为空，则报错
	top();//返回栈顶
		stk.top()=6;//修改栈顶为6
	empty();

（5）queue

先进先出

	size();
	push();
	pop();
	front();
	back();
	empty();

优先队列

	poriority_queue<int>q;//默认大根堆，即less<int>
	poriority_queue<int,vector<int>,greater<int>>q;//小根堆
	结构体定义
	struct node
	{
		int x,y;
		friend bool operator<(const node &x,const node &y){
			return x.x<y.x;
		}
	};//按照x从大到小
	poriority_queue<node>q;//引用
	size();
	push();
	pop();
	top();
	empty();

（6）set

6.1> set

	insert();
	erase();
		s.erase(3);//删除元素3
		s.erase(s.begin()); // 删除指点迭代器的元素
		s.erasse(s.begin(), s.begin() + 2); // 删除连个迭代器范围内的数
	size();
	empty();
	count();
		s.count(3);//元素3是否存在
	clear();//O(n)
	lower_bound();//log(n)
		s.lower_bound(3)//找到 第一个 >= 3 的迭代器，没有则返回end()
	upper_bound();//log(n)
		s.upper_bound(3)//找到 第一个  > 3 的迭代器，没有则返回end()
	find();//返回查找元素的迭代器，没有则返回end()

6.2> unordered_set

	存入set中，但不排序，无lower_bound()等操作

6.3> multiset

	排序，不去重
	erase();//仍是擦除所有这个元素
	可以multiset<node,cmp>s;//大部分容器应该都有相似的
	equal_range(elem);//返回元素值等于elem的区间(两个迭代器)（l 与 r+1 的位置的元素）
	swap();
		a.swap(b);
		swap(a,b);
	s.begin();
	s.end();
	s.rbegin();
	s.rend();
	
	insert();
	erase();
	clear();
	
	emplace();
		//相当于insert，但速度更快？
		//set与unordered_set好像也能用
	count();

（7）map

	erase();
	count();
	size();
	empty();
	clear();
	lower_bound();
		如 mp.lower_bound(3);
	upper_bound();

	unordered_map
	速度快，但键不能为结构体类型

（8）bitset

	bitset<10> name; //声明 10 位，每位都是0
	bitset<N> name(string 或 char[] );//如"100110"，只包含0和1
	// 定义长度为 N 的二进制数组，命名为 name，将01串 string 存到其中，长度不够前补 0，长度过长截断；
	bitset<N> name(int);//如：4
	//若 N=2，则name = 00，(4: 100) 
	
	count()  返回有多少个1

    any()  判断是否至少有一个1
    none()  判断是否全为0

    set()  把所有位置成1
    set(k, v)  将第k位变成v
    reset()  把所有位变成0
    flip()  等价于~
    flip(k) 把第k位取反

（9）deque

	双端队列，相较于queue，有
	push_front();
	pop_front();
	push_back();
	pop_back();

（10）list

相当于双链表

	push_front(val)//在头部插入
	pop_front()//在头部删除
	push_back(val)//尾部插入
	pop_back()//尾部删除
	insert(iterator, val)//在迭代器iterator前插入val
	insert(iterator, count, val)//在迭代器iterator前插入count个val
	front()、back()//返回头元素、尾元素的引用
	begin()、end()//返回头部和尾部下一位置的迭代器
	size()//大小
	sort()//升序排序
	clear()//清空
	reverse()//翻转链表
	merge(list2) //用第二个有序的 list 合并一个有序 list
	splice(list.iterator, list2, list2.iterator_start, list2.iterator_end)
		//在本list的 iterator后插入list2的从 iterator_start 到 iterator_end， 
		//后面两个可填可以不填，当填了iterator_start，可不填最后一个，时间复杂度O(1)
	erase(iterator)：删除iterator，返回删除前的下一个的迭代器
	erase(iterator_start, iterator_end)
		//删除[iterator_start, iterator_end)范围内的元素，返回删除前的	iterator_end

（11）tuple

	类似于pair,但能存很多个
	tuple<int, string, double, char> t = {1, "okok", 0.9, 'y'};
	
	cout << get<0>(t) << endl; // 输出：1
	
	auto [a, b, c, d] = t;
	cout << a << ' ' << b << ' ' << c << ' ' << d << endl; // 输出：1 okok 0.9 y

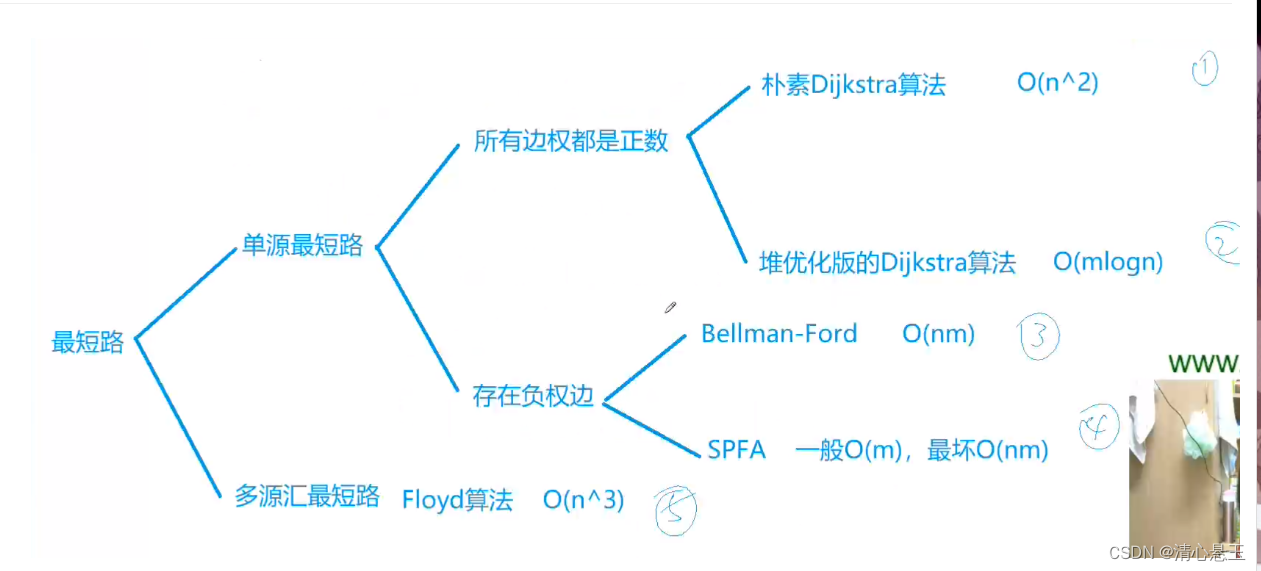
三、图论

最小生成树问题：prim 与 kruskal

13. 拓扑排序（topsort）

时间复杂度 O(n+m)，n 表示点数，m表示边数

	bool topsort()
	{
	    int hh = 0, tt = -1;
	
	    // d[i] 存储点i的入度
	    for (int i = 1; i <= n; i ++ )
	        if (!d[i])
	            q[ ++ tt] = i;
	
	    while (hh <= tt)
	    {
	        int t = q[hh ++ ];
	
	        for (int i = h[t]; i != -1; i = ne[i])
	        {
	            int j = e[i];
	            if (-- d[j] == 0)
	                q[ ++ tt] = j;
	        }
	    }
	
	    // 如果所有点都入队了，说明存在拓扑序列；否则不存在拓扑序列。
	    return tt == n - 1;
	}

14. dijkstra

时间复杂度 O(mlogn)，n 表示点数，m表示边数

	typedef pair<int, int> PII;

	int n;      // 点的数量
	int h[N], w[N], e[N], ne[N], idx;       // 邻接表存储所有边
	int dist[N];        // 存储所有点到1号点的距离
	bool st[N];     // 存储每个点的最短距离是否已确定
	
	// 求1号点到n号点的最短距离，如果不存在，则返回-1
	int dijkstra()
	{
	    memset(dist, 0x3f, sizeof dist);
	    dist[1] = 0;
	    priority_queue<PII, vector<PII>, greater<PII>> heap;
	    heap.push({0, 1});      // first存储距离，second存储节点编号
	
	    while (heap.size())
	    {
	        auto t = heap.top();
	        heap.pop();
	
	        int ver = t.second, distance = t.first;
	
	        if (st[ver]) continue;
	        st[ver] = true;
	
	        for (int i = h[ver]; i != -1; i = ne[i])
	        {
	            int j = e[i];
	            if (dist[j] > distance + w[i])
	            {
	                dist[j] = distance + w[i];
	                heap.push({dist[j], j});
	            }
	        }
	    }
	
	    if (dist[n] == 0x3f3f3f3f) return -1;
	    return dist[n];
	}

15. spfa

队列优化的Bellman-Ford算法
时间复杂度平均情况下 O(m)，最坏情况下 O(nm)，n表示点数，m表示边数

	int n;      // 总点数
	int h[N], w[N], e[N], ne[N], idx;       // 邻接表存储所有边
	int dist[N];        // 存储每个点到1号点的最短距离
	bool st[N];     // 存储每个点是否在队列中
	
	// 求1号点到n号点的最短路距离，如果从1号点无法走到n号点则返回-1
	int spfa()
	{
	    memset(dist, 0x3f, sizeof dist);
	    dist[1] = 0;
	
	    queue<int> q;
	    q.push(1);
	    st[1] = true;
	
	    while (q.size())
	    {
	        auto t = q.front();
	        q.pop();
	
	        st[t] = false;
	
	        for (int i = h[t]; i != -1; i = ne[i])
	        {
	            int j = e[i];
	            if (dist[j] > dist[t] + w[i])
	            {
	                dist[j] = dist[t] + w[i];
	                if (!st[j])     // 如果队列中已存在j，则不需要将j重复插入
	                {
	                    q.push(j);
	                    st[j] = true;
	                }
	            }
	        }
	    }
	
	    if (dist[n] == 0x3f3f3f3f) return -1;
	    return dist[n];
	}

spfa判断图中是否存在负环
O(nm)

	int n;      // 总点数
	int h[N], w[N], e[N], ne[N], idx;       // 邻接表存储所有边
	int dist[N], cnt[N];        // dist[x]存储1号点到x的最短距离，cnt[x]存储1到x的最短路中经过的点数
	bool st[N];     // 存储每个点是否在队列中
	
	// 如果存在负环，则返回true，否则返回false。
	bool spfa()
	{
	    // 不需要初始化dist数组
	    // 原理：如果某条最短路径上有n个点（除了自己），
	    //		那么加上自己之后一共有n+1个点，由抽屉原理一定有两个点相同，所以存在环。
	
	    queue<int> q;
	    for (int i = 1; i <= n; i ++ )
	    {
	        q.push(i);
	        st[i] = true;
	    }
	
	    while (q.size())
	    {
	        auto t = q.front();
	        q.pop();
	
	        st[t] = false;
	
	        for (int i = h[t]; i != -1; i = ne[i])
	        {
	            int j = e[i];
	            if (dist[j] > dist[t] + w[i])
	            {
	                dist[j] = dist[t] + w[i];
	                cnt[j] = cnt[t] + 1;
	                if (cnt[j] >= n) return true;
	                	// 如果从1号点到x的最短路中包含至少n个点（不包括自己），则说明存在环
	                if (!st[j])
	                {
	                    q.push(j);
	                    st[j] = true;
	                }
	            }
	        }
	    }
	
	    return false;
	}

16. 染色法判断二分图

O(n+m)

	int n;      // n表示点数
	int h[N], e[M], ne[M], idx;     // 邻接表存储图
	int color[N];       // 表示每个点的颜色，-1表示未染色，0表示白色，1表示黑色
	
	// 参数：u表示当前节点，c表示当前点的颜色
	bool dfs(int u,int c)//染色
	{
	    color[u]=c;
	    for(int i=h[u];~i;i=ne[i])
	    {
	        int j=e[i];
	        if(color[j])
			{
				if(color[j]==color[u]) return false;
			}
			else if(!dfs(j,!c)) return false;
	    }
	    return true;
	}
	
	bool check()//判断是否是二分图
	{
	    memset(color,-1,sizeof color);
	    for(int i=1;i<=n;i++)
	        if(color[i]==-1)
	            if(!dfs(i, 0)) return false;
	    return true;
	}

17. 匈牙利算法

O(nm)
（二分图最大匹配）

	int n1, n2;     // n1表示第一个集合中的点数，n2表示第二个集合中的点数
	int h[N], e[M], ne[M], idx;     // 邻接表存储所有边，匈牙利算法中只会用到从第一个集合指向第二个集合的边，所以这里只用存一个方向的边
	int match[N];       // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
	bool st[N];     // 表示第二个集合中的每个点是否已经被遍历过
	
	bool find(int x)
	{
	    for (int i = h[x]; i != -1; i = ne[i])
	    {
	        int j = e[i];
	        if (!st[j])
	        {
	            st[j] = true;
	            if (match[j] == 0 || find(match[j]))
	            {
	                match[j] = x;
	                return true;
	            }
	        }
	    }
	
	    return false;
	}
	
	// 求最大匹配数，依次枚举第一个集合中的每个点能否匹配第二个集合中的点
	int res = 0;
	for (int i = 1; i <= n1; i ++ )
	{
	    memset(st, false, sizeof st);
	    if (find(i)) res ++ ;
	}

四、数学知识

18. 线性筛素数

	int primes[N], cnt;     // primes[]存储所有素数
	bool st[N];         // st[x]存储x是否被筛掉
	
	void get_primes(int n)
	{
	    for (int i = 2; i <= n; i ++ )
	    {
	        if (!st[i]) primes[cnt ++ ] = i;
	        for (int j = 0; primes[j] <= n / i; j ++ )
	        {
	            st[primes[j] * i] = true;
	            if (i % primes[j] == 0) break;
	        }
	    }
	}

19. 约数个数和约数之和

	如果 N = p1^c1 * p2^c2 * ... *pk^ck
	约数个数： (c1 + 1) * (c2 + 1) * ... * (ck + 1)
	约数之和： (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)

20. 欧拉函数

$a^b\equiv \begin{cases} a^{b\ mod\ \varphi(m)},\quad \quad \quad \ gcd(a,m)=1,\\ a^b, \quad \quad \quad \quad \ \quad \quad \ gcd(a,m)\neq1,b<\varphi(m),\quad (mod\ m)\\ a^{b\ mod\ \varphi(m)+\varphi(m)},\quad gcd(a,m)\neq1,b\geq\varphi(m). \end{cases}$

	int phi(int x)
	{
	    int res = x;
	    for (int i = 2; i <= x / i; i ++ )
	        if (x % i == 0)
	        {
	            res = res / i * (i - 1);
	            while (x % i == 0) x /= i;
	        }
	    if (x > 1) res = res / x * (x - 1);
	
	    return res;
	}

筛法求欧拉函数

	int primes[N], cnt;     // primes[]存储所有素数
	int euler[N];           // 存储每个数的欧拉函数
	bool st[N];         // st[x]存储x是否被筛掉
	
	
	void get_eulers(int n)
	{
	    euler[1] = 1;
	    for (int i = 2; i <= n; i ++ )
	    {
	        if (!st[i])
	        {
	            primes[cnt ++ ] = i;
	            euler[i] = i - 1;
	        }
	        for (int j = 0; primes[j] <= n / i; j ++ )
	        {
	            int t = primes[j] * i;
	            st[t] = true;
	            if (i % primes[j] == 0)
	            {
	                euler[t] = euler[i] * primes[j];
	                break;
	            }
	            euler[t] = euler[i] * (primes[j] - 1);
	        }
	    }
	}

21. 扩展欧几里得算法

判断方程ax+by=m是否有解
求ax+by=m的任意一组解、通解、最小整数解
求逆元

如果ax+by=m有解，那么m一定是gcd(a,b)的若干倍

扩欧求出来的解x，y是方程：ax+by=gcd(a,b)的解

	int x,y,kx,ky;
	int g=extgcd(a,b,x,y);
	x*=c/g;
	y*=c/g;
	kx=b/g;
	ky=-a/g;
	//通解就是：x+kx*n,y+ky*n
	//即，x+b/g*n, y-a/g*n

	//最小正整数解
	int x,y;
	int g=extgcd(a,b,x,y);
	x*=c/g;
	b/=g;
	if(b<0)b=-b;
	int ans=x%b;
	if(ans<0)ans+=b;

	// 求x, y，使得ax + by = gcd(a, b)
	int exgcd(int a, int b, int &x, int &y)
	{
	    if (!b)
	    {
	        x = 1; y = 0;
	        return a;
	    }
	    int d = exgcd(b, a % b, y, x);
	    y -= (a/b) * x;
	    return d;
	}

22. 高斯消元 — 高斯消元解线性方程组

// a[N][N]是增广矩阵
int gauss()
{
    int c, r;
    for (c = 0, r = 0; c < n; c ++ )
    {
        int t = r;
        for (int i = r; i < n; i ++ )   // 找到绝对值最大的行
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;

        if (fabs(a[t][c]) < eps) continue;

        for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]);      // 将绝对值最大的行换到最顶端
        for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];      // 将当前行的首位变成1
        for (int i = r + 1; i < n; i ++ )       // 用当前行将下面所有的列消成0
            if (fabs(a[i][c]) > eps)
                for (int j = n; j >= c; j -- )
                    a[i][j] -= a[r][j] * a[i][c];

        r ++ ;
    }

    if (r < n)
    {
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][n]) > eps)
                return 2; // 无解
        return 1; // 有无穷多组解
    }

    for (int i = n - 1; i >= 0; i -- )
        for (int j = i + 1; j < n; j ++ )
            a[i][n] -= a[i][j] * a[j][n];

    return 0; // 有唯一解
    /*
    //唯一解如下
    	for (int i = 0; i < n; i ++ )
        {
            if(fabs(a[i][n]) < eps) a[i][n] = 0.00; // 避免输出-0.00
            printf("%.2lf\n", a[i][n]);

        }
    */
}

23. 组合数

（0）线性求逆元

	inv[1]=1;
	for(i=2;i<=n;i++)
		inv[i] = ( p - p / i ) * inv[p % i] % p;

（1）递推法求组合数

	// c[a][b] 表示从a个苹果中选b个的方案数
	for (int i = 0; i < N; i ++ )
	    for (int j = 0; j <= i; j ++ )
	        if (!j) c[i][j] = 1;
	        else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;

（2）通过预处理逆元的方式求组合数

	//线性求阶乘逆元
	fact[0]=1;
	for(int i=1;i<N;i++)
		fact[i]=fact[i-1]*i%mod;
	infact[N-1]=qmi(fact[N-1],mod-2);
	for(int i=N-2;i>=0;i--)
		infact[i]=fact[i+1]*(i+1)%mod;

（3）Lucas定理

	若p是质数，则对于任意整数 1 <= m <= n，有：
    C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p)

	int C(int a, int b, int p)  // 通过定理求组合数C(a, b)
	{
	    if (a < b) return 0;
	
	    LL x = 1, y = 1;  // x是分子，y是分母
	    for (int i = a, j = 1; j <= b; i --, j ++ )
	    {
	        x = x * i % p;
	        y =  y * j % p;
	    }
	
	    return x * qmi(y, p - 2, p) % p;
	}
	
	int lucas(LL a, LL b, int p)
	{
	    if (a < p && b < p) return C(a, b, p);
	    return C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
	}

（4）分解质因数法求组合数

当我们需要求出组合数的真实值，而非对某个数的余数时，分解质因数的方式比较好用：
    1. 筛法求出范围内的所有质数
    2. 通过 C(a, b) = a! / b! / (a - b)! 这个公式求出每个质因子的次数。 
        n! 中p的次数是 n / p + n / p^2 + n / p^3 + ...
    3. 用高精度乘法将所有质因子相乘

int primes[N], cnt;     // 存储所有质数
int sum[N];     // 存储每个质数的次数
bool st[N];     // 存储每个数是否已被筛掉


void get_primes(int n)      // 线性筛法求素数
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


int get(int n, int p)       // 求n！中的次数
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}


vector<int> mul(vector<int> a, int b)       // 高精度乘低精度模板
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }

    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }

    return c;
}

get_primes(a);  // 预处理范围内的所有质数

for (int i = 0; i < cnt; i ++ )     // 求每个质因数的次数
{
    int p = primes[i];
    sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}

vector<int> res;
res.push_back(1);

for (int i = 0; i < cnt; i ++ )     // 用高精度乘法将所有质因子相乘
    for (int j = 0; j < sum[i]; j ++ )
        res = mul(res, primes[i]);

24. 卡特兰数

前?个卡特兰数
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …

初级应用：
给定n个0和n个1，它们按照某种顺序排成长度为2n的序列，满足任意前缀中0的个数都不少于1的个数的序列的数量为： 
Cat(n) = C(2n, n) / (n + 1)

通项公式1： $h_n=\frac{1}{n+1}C_{2n}^n=\frac{(2n)!}{(n+1)!n!}$

通项公式2： $h_n=\frac{1}{n+1}\sum_{i=0}^{n}(C_n^i)^2$

递推公式1： $h_{n+1}=\frac{4n+2}{n+2}h_n,\quad \quad \quad \ \ h_0=1$

递推公式2： $h_{n+1}=\sum_{i=0}^{n}h_ih_{n-i}, \quad \ h_0=1,n>=0$

性质： $h_n=C_{\ 2n}^{\ n}-C_{\ 2n}^{\ n-1}=C_{\ 2n}^{\ n}-C_{\ 2n}^{\ n+1}$

（1）出栈次序

一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?
其解等于第 n 个Catalan数

（2）01序列

给出一个n，要求一个长度为2n的01序列，使得序列的任意前缀中1的个数不少于0的个数，有多少个不同的01序列?
其解等于第 n 个Catalan数

（3）+1，-1序列

n个+1和n个-1构成的2n项 $a_1,a_2, ···,a_{2n}$ ，其部分和满足非负性质，即 $a_1+a_2+···+a_k \geq 0$ ，有多少个不同的此序列?
其解等于第 n 个Catalan数

（4）括号序列

n对括号有多少种匹配方式？
其解等于第 n 个Catalan数

（5）找零问题

2n个人要买票价为五元的电影票，每人只买一张，但是售票员没有钱找零。其中，n个人持有五元，另外n个人持有十元，问在不发生找零困难的情况下，有多少种排队方法？
其解等于第 n 个Catalan数

（6）矩阵链乘

P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？
其解等于第 n - 1 个Catalan数

（7）二叉树计数

有n个节点构成的二叉树（非叶子节点都有2个儿子），共有多少种情形？
有n+1个叶子的二叉树的个数？
其解等于第 n 个Catalan数

（8）凸多边形划分

在一个n边形中，通过不相交于n边形内部的对角线，把n边形拆分为若干个三角形，问有多少种拆分方案？
其解等于第 n - 2 个Catalan数

（9）圆上n条线段

在圆上选择2n个点，将这些点成对连接起来使得所得到的n条线段不相交的方法数？
其解等于第 n 个Catalan数

（10）单调路径

一位大城市的律师在他住所以北n个街区和以东n个街区处工作，每天他走2n个街区去上班。如果他从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？
其解等于第 n 个Catalan数

（11）填充阶梯图形

用n个长方形填充一个高度为n的阶梯状图形的方法个数？

其解等于第 n 个Catalan数

（12）摞碗问题

饭后，姐姐洗碗，妹妹把姐姐洗过的碗一个一个放进碗橱摞成一摞。一共有n个不同的碗，洗前也是摞成一摞的，也许因为小妹贪玩而使碗拿进碗橱不及时，姐姐则把洗过的碗摞在旁边，问：小妹摞起的碗有多少种可能的方式？
其解等于第 n 个Catalan数

（13）汽车胡同加油问题

一个汽车队在狭窄的路面上行驶，不得超车，但可以进入一个死胡同去加油，然后再插队行驶，共有n辆汽车，问共有多少种不同的方式使得车队开出城去？
其解等于第 n 个Catalan数

（14）还书借书问题

在图书馆一共2n个人在排队，n个还《面试宝典》一书，n个在借《面试宝典》一书，图书馆此时没有了面试宝典了，求他们排队的总数？
其解等于第 n 个Catalan数

（15）高矮排队问题

2n个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
其解等于第 n 个Catalan数

五、提高

25. 矩阵乘法

斐波那契数列前n项和

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3;
int n,m;
void mul(int c[][N],int a[][N],int b[][N])
{
    int temp[N][N]={0};
    for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
            for(int k=0;k<N;k++)
                temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%m;
    memcpy(c,temp,sizeof temp);
}
signed main()
{
    cin>>n>>m;
    int f1[N][N]={1,1,1};
    int a[N][N]={
      {0,1,0},
      {1,1,1},
      {0,0,1}
    };
    n--;
    while(n)
    {
        if(n&1) mul(f1,f1,a);
        mul(a,a,a);
        n>>=1;
    }
    cout<<f1[0][2];
    return 0;
}

$T(n)=(F1+2F_2+3F_3+…+nF_n)\ mod\ m$

signed main()
{
    cin>>n>>m;
    int f1[N][N]={1,1,1,1},x=n+1;
    int a[N][N]={
      {0,1,0,0},
      {1,1,1,1},
      {0,0,1,1},
      {0,0,0,1}
    };
    n--;
    while(n)
    {
        if(n&1) mul(f1,f1,a);
        mul(a,a,a);
        n>>=1;
    }
    cout<<(f1[0][2]*x-f1[0][3]+m)%m;
    return 0;
}

26. 树状数组

一个简单的整数问题2

给定一个长度为 N 的数列 A，以及 M 条指令，每条指令可能是以下两种之一：

C l r d，表示把 A[l],A[l+1],…,A[r] 都加上 d。
Q l r，表示询问数列中第 l∼r 个数的和。

对于每个询问，输出一个整数表示答案。

#include<bits/stdc++.h>
#define int long long
#define endl "\n"
using namespace std;
const int N=1e5+10;
int n,m,a[N];
int tr1[N],tr2[N];
int lowbit(int x)
{
    return x & -x;
}
void add(int tr[],int x,int c)
{
    for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
}
int sum(int tr[],int x)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i)) res+=tr[i];
    return res;
}
int prefix_sum(int x)
{
    return sum(tr1,x)*(x+1)-sum(tr2,x);
}
signed main()
{
    ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        add(tr1,i,a[i]-a[i-1]);
        add(tr2,i,(a[i]-a[i-1])*i);
    }
    while(m--)
    {
        char op[2];
        int l,r,d;
        cin>>op>>l>>r;
        if(*op=='Q')
        {
            cout<<prefix_sum(r)-prefix_sum(l-1)<<endl;
        }
        else
        {
            cin>>d;
            add(tr1,l,d),add(tr2,l,l*d);
            add(tr1,r+1,-d),add(tr2,r+1,(r+1)*-d);
        }
    }
    return 0;
}

27. 线段树

（1）区间最大公约数

给定一个长度为 N 的数列 A，以及 M 条指令，每条指令可能是以下两种之一：

C l r d，表示把 A[l],A[l+1],…,A[r] 都加上 d。
Q l r，表示询问 A[l],A[l+1],…,A[r] 的最大公约数(GCD)。

对于每个询问，输出一个整数表示答案。

#include<bits/stdc++.h>
#define int long long 
#define endl "\n"
using namespace std;
const int N=500010;
int n,m,a[N];
struct Node
{
    int l,r;
    int sum,gcd;
}tr[N*4];

void pushup(Node &root,Node &left,Node &right)
{
    root.sum=left.sum+right.sum;
    root.gcd=__gcd(left.gcd,right.gcd);
}

void pushup(int u)
{
    pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}

void build(int u,int l,int r)
{
    if(l==r)
    {
        int b=a[r]-a[r-1];
        tr[u]={l,r,b,b};
    }
    else
    {
        tr[u]={l,r};
        int mid=l+r>>1;
        build(u<<1,l,mid),build(u<<1|1,mid+1,r);
        pushup(u);
    }
}

void modify(int u,int x,int v)
{
    if(tr[u].l==x&&tr[u].r==x)
    {
        int b=tr[u].sum+v;
        tr[u]={x,x,b,b};
    }
    else
    {
        int mid=tr[u].l+tr[u].r>>1;
        if(x<=mid) modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        pushup(u);
    }
}

Node query(int u,int l,int r)
{
    if(l>r) return {0};
    if(tr[u].l>=l&&tr[u].r<=r) return tr[u];
    else
    {
        int mid=tr[u].l+tr[u].r>>1;
        Node res={0},num={0};
        if(l<=mid) res=query(u<<1,l,r);
        if(mid<r) num=query(u<<1|1,l,r);
        pushup(res,res,num);
        return res;
    }
}

signed main()
{
    ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    build(1,1,n);
    while(m--)
    {
        char op[2];
        int l,r,d;
        cin>>op>>l>>r;
        if(*op=='Q')
        {
            auto left=query(1,1,l),right=query(1,l+1,r);
            cout<<abs(__gcd(left.sum,right.gcd))<<endl;
        }
        else
        {
            cin>>d;
            modify(1,l,d);
            if(r+1<=n) modify(1,r+1,-d);
        }
    }
    return 0;
}

（2）一个简单的整数问题2

给定一个长度为 N 的数列 A，以及 M 条指令，每条指令可能是以下两种之一：

C l r d，表示把 A[l],A[l+1],…,A[r] 都加上 d。
Q l r，表示询问数列中第 l∼r 个数的和。

对于每个询问，输出一个整数表示答案。

#include<bits/stdc++.h>
#define int long long
#define endl "\n"
using namespace std;
const int N=1e5+10;
int n,m,w[N];

struct Node
{
    int l,r;
    int sum,add;
}tr[N*4];

void pushup(int u)
{
    tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}

void pushdown(int u)
{
    auto &root=tr[u],&left=tr[u<<1],&right=tr[u<<1|1];
    if(root.add)
    {
        left.add+=root.add;
        left.sum+=root.add*(left.r-left.l+1);
        right.add+=root.add;
        right.sum+=root.add*(right.r-right.l+1);
        root.add=0;
    }
}

void build(int u,int l,int r)
{
    if(l==r) tr[u]={l,r,w[r],0};
    else
    {
        tr[u]={l,r};
        int mid=l+r>>1;
        build(u<<1,l,mid),build(u<<1|1,mid+1,r);
        pushup(u);
    }
}

void modify(int u,int l,int r,int d)
{
    if(tr[u].l>=l&&tr[u].r<=r)
    {
        tr[u].sum+=d*(tr[u].r-tr[u].l+1);
        tr[u].add+=d;
    }
    else
    {
        pushdown(u);
        int mid=tr[u].l+tr[u].r>>1;
        if(l<=mid) modify(u<<1,l,r,d);
        if(mid<r) modify(u<<1|1,l,r,d);
        pushup(u);
    }
}

int query(int u,int l,int r)
{
    if(tr[u].l>=l&&tr[u].r<=r) return tr[u].sum;
    else
    {
        pushdown(u);
        int mid=tr[u].l+tr[u].r>>1;
        int res=0;
        if(l<=mid) res=query(u<<1,l,r);
        if(mid<r) res+=query(u<<1|1,l,r);
        return res;
    }
}

signed main()
{
    ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>w[i];
    build(1,1,n);
    while(m--)
    {
        int l,r,d;
        char op[2];
        cin>>op>>l>>r;
        if(*op=='C')
        {
            cin>>d;
            modify(1,l,r,d);
        }
        else
        {
            cout<<query(1,l,r)<<endl;
        }
    }
    return 0;
}

（3）维护序列

有长为 N 的数列，不妨设为 a1,a2,…,aN。

有如下三种操作形式：

把数列中的一段数全部乘一个值；
把数列中的一段数全部加一个值；
询问数列中的一段数的和，由于答案可能很大，你只需输出这个数模 P 的值。

#include<bits/stdc++.h>
#define int long long
#define endl "\n"
using namespace std;
const int N=1e5+10;
int n,m,p,w[N];
struct Node
{
    int l,r;
    int sum,add,mul;
}tr[N*4];

void pushup(int u)
{
    tr[u].sum=(tr[u<<1].sum+tr[u<<1|1].sum)%p;
}

void eval(Node &t,int add,int mul)
{
    t.sum=(t.sum*mul+add*(t.r-t.l+1))%p;
    t.add=(t.add*mul+add)%p;
    t.mul=(t.mul*mul)%p;
}

void pushdown(int u)
{
    auto &root=tr[u],&left=tr[u<<1],&right=tr[u<<1|1];
    eval(left,root.add,root.mul);
    eval(right,root.add,root.mul);
    root.add=0,root.mul=1;
}

void build(int u,int l,int r)
{
    if(l==r) tr[u]={l,r,w[r],0,1};
    else
    {
        tr[u]={l,r,0,0,1};
        int mid=l+r>>1;
        build(u<<1,l,mid),build(u<<1|1,mid+1,r);
        pushup(u);
    }
}

void modify(int u,int l,int r,int add,int mul)
{
    if(tr[u].l>=l&&tr[u].r<=r) eval(tr[u],add,mul);
    else
    {
        pushdown(u);
        int mid=tr[u].l+tr[u].r>>1;
        if(l<=mid) modify(u<<1,l,r,add,mul);
        if(mid<r) modify(u<<1|1,l,r,add,mul);
        pushup(u);
    }
}

int query(int u,int l,int r)
{
    if(tr[u].l>=l&&tr[u].r<=r) return tr[u].sum;
    else
    {
        pushdown(u);
        int mid=tr[u].l+tr[u].r>>1;
        int res=0;
        if(l<=mid) res=query(u<<1,l,r);
        if(mid<r) res=(res+query(u<<1|1,l,r))%p;
        return res;
    }
}

signed main()
{
    ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);
    cin>>n>>p;
    for(int i=1;i<=n;i++) cin>>w[i];
    build(1,1,n);
    cin>>m;
    while(m--)
    {
        int x,l,r,d;
        cin>>x>>l>>r;
        if(x==1)
        {
            cin>>d;
            modify(1,l,r,0,d);
        }
        else if(x==2)
        {
            cin>>d;
            modify(1,l,r,d,1);
        }
        else
        {
            cout<<query(1,l,r)%p<<endl;
        }
    }
    return 0;
}

线段树的第二种询问方式

node query(int u,int l,int r)
{
    if(l<=tr[u].l&&tr[u].r<=r) return tr[u];
    else
    {
        int mid=tr[u].l+tr[u].r>>1;
        if(r<=mid) return query(u<<1,l,r);
        else if(l>mid) return query(u<<1|1,l,r);
        else
        {
            auto left=query(u<<1,l,r);
            auto right=query(u<<1|1,l,r);
            node res;
            pushup(res,left,right);
            return res;
        }
       
    }
}

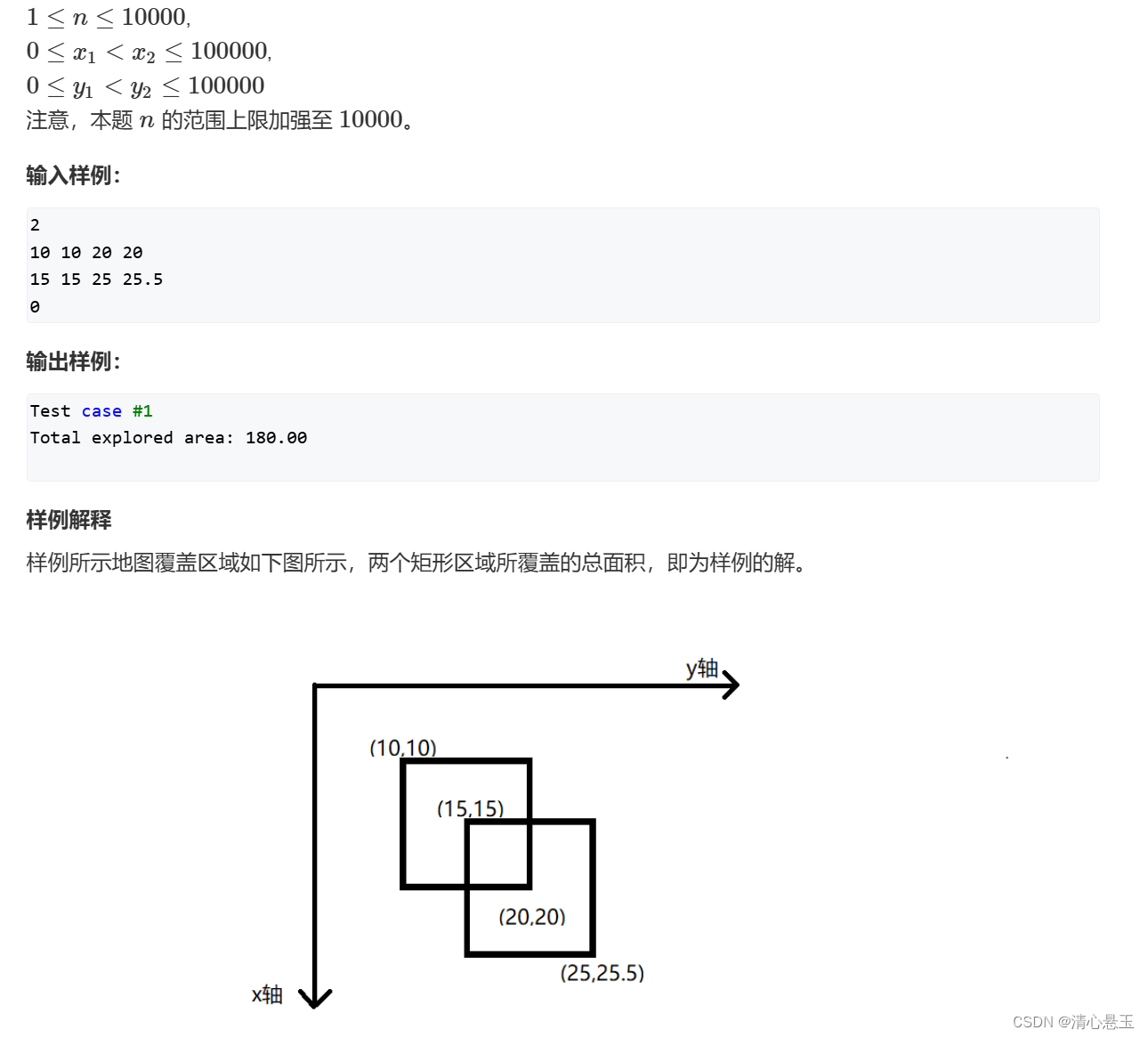
28. 扫描线

求被覆盖的面积

#include<bits/stdc++.h>
#define int long long
#define endl "\n"
using namespace std;
const int N=1e5+10;
int n;
vector<double>ys;
struct Segment
{
    double x,y1,y2;
    int k;
    friend bool operator<(const Segment &x,const Segment &y)
    {
        return x.x<y.x;
    }
}seg[N*2];
struct node
{
    int l,r;
    double len;
    int cnt;
}tr[N*8];

int find(double y)
{
    return lower_bound(ys.begin(),ys.end(),y)-ys.begin();
}

void pushup(int u)
{
    if(tr[u].cnt) tr[u].len=ys[tr[u].r+1]-ys[tr[u].l];
    else if(tr[u].l==tr[u].r) tr[u].len=0;
    else tr[u].len=tr[u<<1].len+tr[u<<1|1].len;
}

void build(int u,int l,int r)
{
    if(l==r) tr[u]={l,r,0,0};
    else
    {
        tr[u]={l,r};
        int mid=l+r>>1;
        build(u<<1,l,mid),build(u<<1|1,mid+1,r);
        // pushup(u);
    }
}

void modify(int u,int l,int r,int k)
{
    if(tr[u].l>=l&&tr[u].r<=r)
    {
        tr[u].cnt+=k;
        pushup(u);
    }
    else
    {
        int mid=tr[u].l+tr[u].r>>1;
        if(l<=mid) modify(u<<1,l,r,k);
        if(mid<r) modify(u<<1|1,l,r,k);
        pushup(u);
    }
}

signed main()
{
    ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);
    int T=1;
    array<double,3>x,y;
    while(cin>>n,n)
    {
        ys.clear();
        for(int i=0,j=0;i<n;i++)
        {
            cin>>x[1]>>y[1]>>x[2]>>y[2];
            seg[j++]={x[1],y[1],y[2],1};
            seg[j++]={x[2],y[1],y[2],-1};
            ys.push_back(y[1]),ys.push_back(y[2]);
        }
        sort(seg,seg+n*2);
        
        sort(ys.begin(),ys.end());
        ys.erase(unique(ys.begin(),ys.end()),ys.end());
        
        build(1,0,ys.size()-2);
        
        double res=0;
        for(int i=0;i<n*2;i++)
        {
            if(i>0) res+=tr[1].len*(seg[i].x-seg[i-1].x);
            modify(1,find(seg[i].y1),find(seg[i].y2)-1,seg[i].k);
        }
        cout<<"Test case #"<<T++<<endl;
        cout<<"Total explored area: "<<fixed<<setprecision(2)<<res<<"\n\n";
    }
    return 0;
}

29. 最近公共祖先（LCA）

#include<bits/stdc++.h>
using namespace std;
const int N=4e4+10,M=N*2;
int n,m,a,b;
int h[N],e[M],ne[M],idx;
int depth[N],fa[N][20];
void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void bfs(int root)
{
    memset(depth,0x3f,sizeof depth);
    depth[0]=0,depth[root]=1;
    queue<int>q;
    q.push(root);
    while(!q.empty())
    {
        auto t=q.front();
        q.pop();
        for(int i=h[t];~i;i=ne[i])
        {
            int j=e[i];
            if(depth[j]>depth[t]+1)
            {
                depth[j]=depth[t]+1;
                q.push(j);
                fa[j][0]=t;
                for(int k=1;k<=19;k++)
                    fa[j][k]=fa[fa[j][k-1]][k-1];
            }
        }
    }
}
int lca(int a,int b)
{
    if(depth[a]<depth[b]) swap(a,b);
    for(int k=15;k>=0;k--)
        if(depth[fa[a][k]]>=depth[b])
            a=fa[a][k];
    if(a==b) return a;
    for(int k=15;k>=0;k--)
        if(fa[a][k]!=fa[b][k])
        {
            a=fa[a][k];
            b=fa[b][k];
        }
    return fa[a][0];
}
int main()
{
    int root=0;
    cin>>n;
    memset(h,-1,sizeof h);
    for(int i=0;i<n;i++)
    {
        cin>>a>>b;
        if(b==-1) root=a;
        else add(a,b),add(b,a);
    }
    bfs(root);
    cin>>m;
    while(m--)
    {
        cin>>a>>b;
        int p=lca(a,b);
        if(p==a) cout<<"1\n";
        else if(p==b) cout<<"2\n";
        else cout<<"0\n";
    }
    return 0;
}

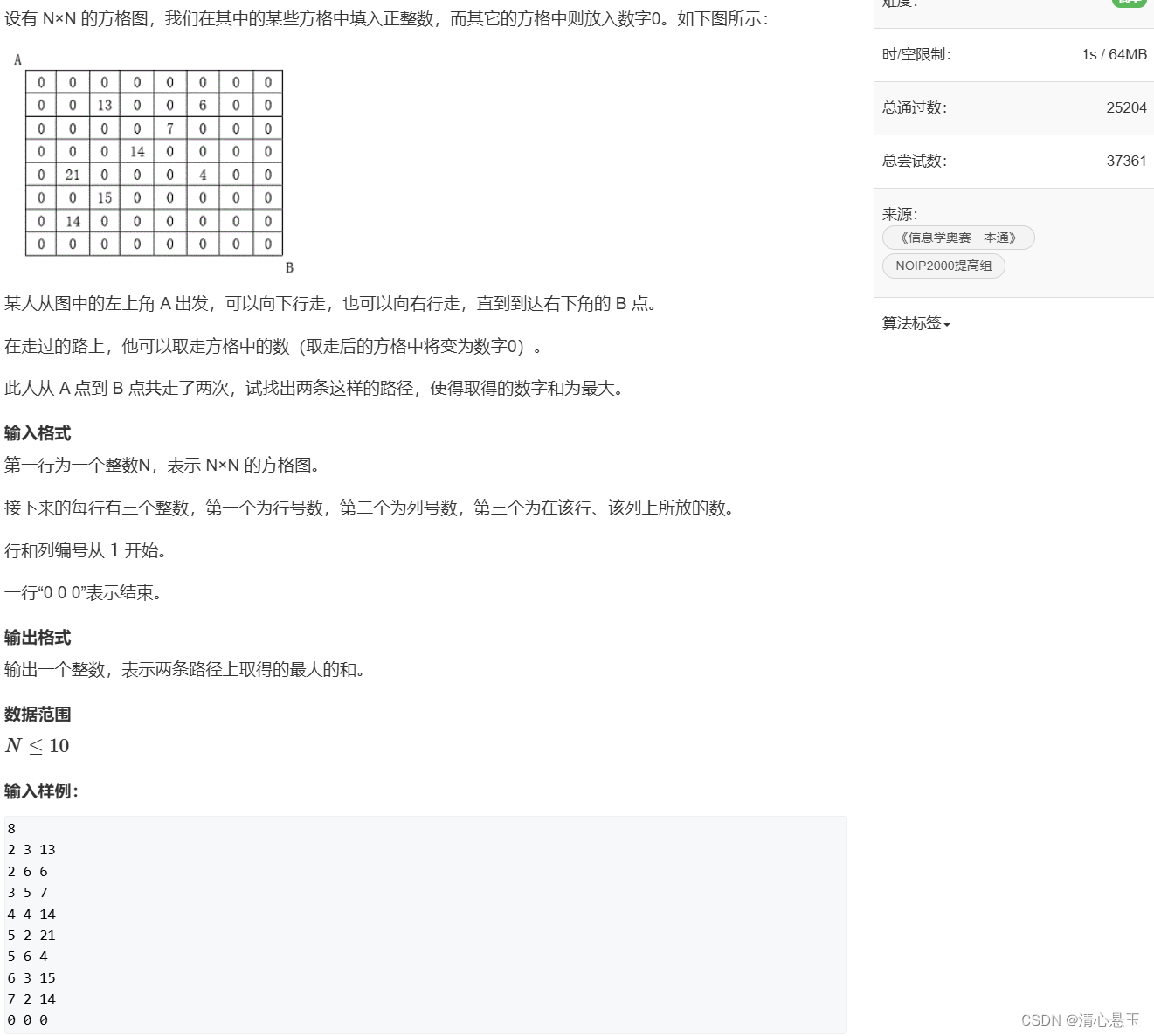
30. 方格取数

在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
const int N=15;
int n,a,b,c;
int w[N][N];
int f[N*2][N][N];
int main()
{
    cin>>n;
    while(cin>>a>>b>>c) w[a][b]=c;
    for(int k=2;k<=n+n;k++)
        for(int i1=1;i1<=n;i1++)
            for(int i2=1;i2<=n;i2++)
            {
                int j1=k-i1,j2=k-i2;
                if(j1>=1&&j1<=n&&j2>=1&&j2<=n)
                {
                    int t=w[i1][j1];
                    if(i1!=i2) t+=w[i2][j2];
                    int &x=f[k][i1][i2];
                    x=max(x,f[k-1][i1-1][i2-1]+t);
                    x=max(x,f[k-1][i1][i2-1]+t);
                    x=max(x,f[k-1][i1-1][i2]+t);
                    x=max(x,f[k-1][i1][i2]+t);
                }
            }
    cout<<f[n+n][n][n]<<endl;
    return 0;
}

31. 最长上升子序列

n ( log₂n )

#include<bits/stdc++.h>
using namespace std;
int a[100010],n,x,f[100010],g[100010],len,cnt;
int main()
{
	while(cin>>x) a[n++]=x;
	for(int i=0;i<n;i++)
	{
		int pos1=upper_bound(f,f+len,a[i],greater<int>())-f;
		if(pos1==len) f[len++]=a[i];
		else f[pos1]=a[i];
		
		int pos2=lower_bound(g,g+cnt,a[i])-g;
		if(pos2==cnt) g[cnt++]=a[i];
		else g[pos2]=a[i];
	}
	cout<<len<<"\n";//最长上升子序列长度
	cout<<cnt<<"\n";//几个上升子序列成功完全覆盖a数组
	return 0;
}

32. 背包

（1）01背包

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 $i$ 件物品的体积是 $v_i$ ，价值是 $w_i$ 。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

#include<iostream>
#include<algorithm>
using namespace std;
#define int long long
const int N = 1010;
int n,m,v[N],w[N],f[N];
signed main()
{
    ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>v[i]>>w[i];
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

（2）完全背包

有 N 件物品和一个容量是 V 的背包。每种物品都有无限件可用。
第 $i$ 件物品的体积是 $v_i$ ，价值是 $w_i$ 。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

	for(int i=1;i<=n;i++)
        for(int j=v[i];j<=m;j++)
            f[j]=max(f[j],f[j-v[i]]+w[i]);
    cout<<f[m]<<endl;

（3）多重背包

有 N 件物品和一个容量是 V 的背包。
第 $i$ 件物品最多有 $s_i$ 件，每件体积是 $v_i$ ，价值是 $w_i$ 。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

#include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int f[N],n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        int v,w,s;
        cin>>v>>w>>s;
        for(int j=m;j>=0;j--)
        {
            for(int k=0;k<=s&&j>=k*v;k++)
            {
                f[j]=max(f[j],f[j-k*v]+k*w);
            }
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

二进制优化

#include <iostream>
using namespace std;
const int N = 2010;
int n,m;
int f[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        int w,v,s;
        cin>>w>>v>>s;
        for(int k=1;k<=s;k<<=1)
        {
            for(int j=m;j>=w*k;j--)
                f[j]=max(f[j],f[j-w*k]+v*k);
            s-=k;
        }
        if(s>0)
        {
            for(int j=m;j>=w*s;j--)
                f[j]=max(f[j],f[j-w*s]+v*s);
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

单调队列优化

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1010, M = 20010;

int n, m;
int v[N], w[N], s[N];
int f[M], g[M];
int q[M];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i] >> s[i];
    for (int i = 1; i <= n; ++ i)
    {
        memcpy(g, f, sizeof g);
        for (int r = 0; r < v[i]; ++ r)
        {
            int hh = 0, tt = -1;
            for (int j = r; j <= m; j += v[i])
            {
                while (hh <= tt && j - q[hh] > s[i] * v[i]) hh ++ ;
                while (hh <= tt && g[q[tt]] + (j - q[tt]) / v[i] * w[i] <= g[j]) -- tt;
                q[ ++ tt] = j;
                f[j] = g[q[hh]] + (j - q[hh]) / v[i] * w[i];
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

（4）混合背包

在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int n,m;
int f[N];
struct Good
{
    int v,w;
};
int main()
{
    vector<Good>goods;
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {
        int v,w,s;
        cin>>v>>w>>s;
        if(s==-1) s=1;
        if(s==0) s=10000;
        for(int k=1;k<=s;k*=2)
        {
            s-=k;
            goods.push_back({k*v,k*w});
        }
        if(s) goods.push_back({s*v,s*w});
    }
    for(auto good:goods)
    {
        for(int j=m;j>=good.v;j--)
        {
            f[j]=max(f[j],f[j-good.v]+good.w);
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

（5）分组背包

在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n,m;
int f[N],v[N],w[N];
int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {
        int s;
        cin>>s;
        for(int j=0;j<s;j++) cin>>v[j]>>w[j];
        for(int j=m;j>=0;j--)
            for(int k=0;k<s;k++)
                if(j>=v[k])
                    f[j]=max(f[j],f[j-v[k]]+w[k]);
    }
    cout<<f[m]<<endl;
    return 0;
}

（6）背包问题求具体方案

字典序最小的方案
01背包

#include<bits/stdc++.h> 
#define endl "\n"
using namespace std;
const int N=2010;
int n,m,f[N][N],w[N],v[N];
int main( )
{
    ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    for(int i=n;i>=1;i--)
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i+1][j];
            if(j>=v[i]) f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
        }
    int j=m;
    for(int i=1;i<=n;i++)
        if(j>=v[i]&&f[i][j]==f[i+1][j-v[i]]+w[i])
        {
            cout<<i<<' ';
            j-=v[i];
        }
    return 0;
}

（7）试填法

在这里插入图片描述

    cin>>n>>k;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    int res=0;
    for(int i=29;i>=0;i--)
    {
        res+=1<<i;
        int fv=(1<<30)-1;
        for(int j=1;j<=n;j++)
        {
            if((res&w[j])==res)
                fv&=v[j];
        }
        if(fv>k)
            res-=1<<i;
    }
    cout<<res;

33. 二进制枚举全排列

i=10011101(二进制)
for(j=i;j;j=(j-1)&i) 能枚举出i中的1的全排列的所有情况
(只有一个1，只有两个1…只有k个1…的全部情况)

34. 斯特林数

第一类斯特林数
$将 n 个不同的元素分配到 k 个圆排列中，圆不能为空\\\ \\ s_u(n,m)=s_u(n-1,m-1)+s_u(n-1,m)*(n-1)$

在这里插入图片描述

第二类斯特林数

$个相同的盒子中，盒子不能为空\\\ \\ S(n,k)=\frac{1}{k!}\sum_{i=0}^{k}(-1)^i\ C_k^i\ (k-i)^n$
$S (n, m) = S (n - 1, m - 1) + S (n - 1, m) * m$
在这里插入图片描述

化简
$S(n,m)=\sum_{i=0}^{m}\frac{(-1)^{m-i}×i^n}{i!×(m-i)!}$

35. 随机数、for循环优化并查集

随机数：mt19937_64 rng;
for循环优化并查集：

    while(q--)
    {
        int op,l,r;
        cin>>op>>l;
        if(op==1)
        {
            cin>>r;
            for(int k=find(r);k>l;k=find(k))
            {
                int fl=find(l);
                a[fl]=max(a[fl],a[k]);
                p[k]=find(p[k-1]);
            }
        }
        else cout<<a[find(l)]<<endl;
    }

以上部分代码来自acwing

清心悬玉

关注

22
点赞
踩
19

收藏

觉得还不错? 一键收藏
2
评论
C++个人算法模版总结

文章目录一、基础算法1. 归并排序2. 二分计算三次方根3. 高精度加法减法乘法除法4. 二维差分5. 离散化6. 区间合并二、数据结构7. 双链表8. 滑动窗口9. KMP10. 并查集11. 哈希12. STL（1）Lambda函数（内置函数）（2）vector2.1> 基础声明方式2.2> 函数（3）string3.1> 基础声明方式3.2> 函数（4）stack（5）queue（6）set6.1> set6.2> unordered_set6.3>
复制链接

扫一扫