小浩的国际象棋

问题描述

小浩有一个大小为 N×NN×N 的国际象棋棋盘。

有 NN 个主教以之字形的形式放置在棋盘的矩阵上，坐标分别为 (1,1),(2,2),(1,3),(2,4),(1,5),…​(1,1),(2,2),(1,3),(2,4),(1,5),…​。

例如对于 N=4​N=4​，棋盘初始时为：

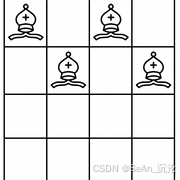
已知主教只能斜向移动且每次可以移动任意距离。

你的任务是找到最少的移

动次数，满足对于所有 1≤i≤N1≤i≤N，棋盘矩阵上的格子 (i,i)​(i,i)​ 都被主教占领了。

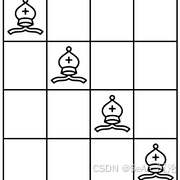
对于 N=4​N=4​，最后的位置应该为：

解释说明：

样例 11：棋盘的主教一开始已经处于最终位置了。

样例 22： 我们最少需要 33 次移动：

• 将主教从 (2,2)(2,2) 移动到 (4,4)(4,4)。
• 将主教从 (1,3)(1,3) 移动到 (2,2)(2,2)。
• 将主教从 (2,4)(2,4) 移动到 (3,3)(3,3)。

样例 3​3​：棋盘的主教一开始已经处于最终位置了。

解题思路：

1.将第二排所有的棋子都移动到最边缘。

2.分奇偶性来讨论第二排棋子的数量，如果N为偶数：第二排棋子的数量为2/N，但偶数时，第二排的最后一个棋子已经在边缘地区，不用移动，所以移动棋子的数量为2/(N-1)的取整，而其他棋子的移动次数为N-2，这个结果不包含第一排的第一个棋子和第二排最后一个棋子，其他的棋子都向斜前方移动即可，最终的公式为：(N-1)/2+N-2；如果N为奇数，可以发现第二排的棋子数量并且移动次数为2/(N-1)，其他步骤也和偶数一样。所以最终的公式总结为(N-1)/2+N-2。

3.此外，我们还需要考虑N与1的关系，如果使用公式，我们需要分情况讨论，直接使用if-else语句来进行，当N>1的时候，使用公式输出。

方法示例：

以下是使用归纳总结之后的Python语言的实现：

T = int(input())
for i in range(T):
    N = int(input())
    if N > 1:
        x = (N - 1) / 2 + N - 2
        print(int(x))
    else:
        print("0")

评测数据规模

对于所有的评测数据，1≤T≤2×1051≤T≤2×105，1≤N≤1091≤N≤109。