图的存储—邻接矩阵和邻接表

---

前言

身为小白的我太容易忘记图的存储了，导致后面对于图论的题目总是很生疏，于是写下这篇文章来加深印象，希望能帮助到正在学习邻接矩阵和邻接表的你。若对文章内容有疑惑，欢迎评论区发言，小白会积极改进的。
参考文献：严蔚敏，吴伟民，数据结构(C语言版)[M].北京：清华大学出版社,2011.

---

一、图的存储结构

在图结构中，节点之间的关系是任意的，图中任意两个数据元素都可能相关，是非线性结构。

所以图没有顺序存储结构，顺序存储结构是借助元素在存储器中的相对位置来表示数据元素之间的逻辑关系的，适用于线性结构。
但是，可以采用邻接矩阵（一个二维数组），来表示元素之间的关系，此外，任意两个顶点都可能存在关系，因此可以使用链表来表示图。

二、邻接矩阵

邻接矩阵是表示顶点之间相邻关系的矩阵。设G(V,E)是具有n个顶点的图，则它的邻接矩阵就是n方阵。

1.邻接矩阵表示法

1.1 图的邻接矩阵

在图中，a[i][j]:表示顶点vi和vj的关系，也就是它们之间有没有边，如果有边就赋值为1，没有边就赋值为0：

举例：

分析：
（1）我们可以发现，在无向图中a[i][j] = a[j][i]，这是为什么呢？
我们要明白a[i][j]，表示的是顶点vi和顶点vj有没有边。在无向图中，若vi和vj之间有边，那么vj和vi之间也有边，都为1；如果没有边，那么都为0。
（2）还可以发现，无论是有向图还是无向图，当i = j我们都会把他赋值为0，将自身到自身视为没有边。
（3）在无向图中，顶点的度为第i行或第i列的元素之和。第i行表示：顶点vi和其他顶点的关系；第i列表示：其他顶点和顶点vi的关系。可以区分入度和出度，但由于是无向图，没有入度和出度之分，所以两者的值是一样的；对于有向图，第i行元素之和就是顶点vi的出度，第j列元素之和就是顶点i的入度。

1.2 网的邻接矩阵

在网（有权值的图）中，a[i][j]:表示顶点vi和vj的关系，如果存在边，那么a[i][j]赋值为它们边的权值，如果没有边，则赋值为∞：

举例：

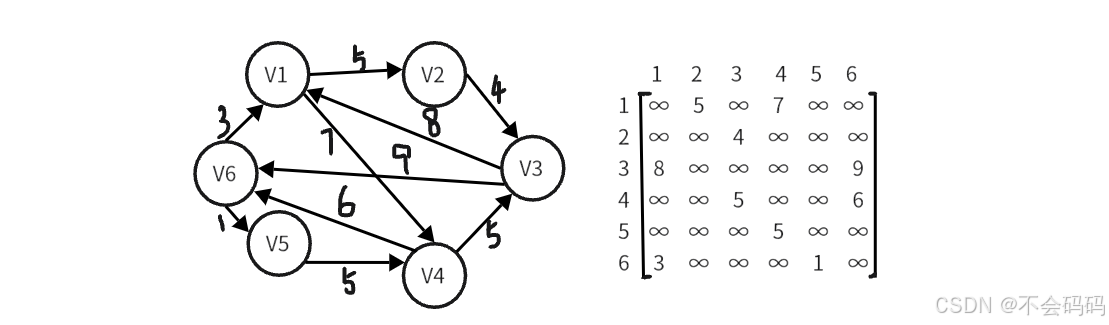
网中除了权值，和默认值与图不同外，其余步骤都相同。

1.3 图的邻接矩阵存储表示

用邻接表表示法表示图，除了一个用于存储邻接矩阵的二维数组外，还需要用一个一维数组来来存储顶点的信息。
形式说明：

#define MaxInt = 32767	// 用于表示∞
#define MaxNum 100	// 最大定点数，因为定义数组需要长度

typedef struct {
   
	char vexs[MaxNum];	// 存储顶点信息的一维数组
	int arcs[MaxNum][MaxNum];	// 定义二维数组，表示邻接矩阵
	int vexnum, arcnum;	// 图的实际顶点数和边数
}AMGraph;	// 因为邻接矩阵单词是:Adjacency Matrix

2.采用邻接矩阵表示法创建无向网

2.1 算法步骤

（1）获取总顶点数和总边数。// 后续操作都与它们有关
（2）初始化邻接矩阵，每个权值初始值都为极大值。
（3）输入每条边依附的顶点（输入的这两个顶点其实就是表示一条边），并输入它的权值，确定两个顶点在图中的位置（也就是获取i和j,这样就可以给a[i][j]赋值，通过函数LocateVex来确定）之后，使其相应边赋予相应的权值，同时使其对应边赋予相同的权值（因为是无向图）。

2.2 算法描述

int LocateVex(AMGraph &G