模板原型 - 基础篇
学习网站
一、进制转换
十进制数 n 转 q 进制
int n,a[1000],len=0;
cin>>n;
do{
a[len++] = n % q;
n /= q;
}while(n>0);
for(int i= len-1;i>=0;i--){
cout<<a[i];
}
p进制数 n 转 Q进制
int y = 0,product = 1; //product 不断乘以p
while( n != 0){
y += (n%10) * product;
n /= 10;
product *= p
}
二、二分查找
① 查找指定元素
// 查找指定元素
int findX(int a[],int l,int r,int x){
int mid;
while( l<= r){ //注意<= 号
mid = (l + r) / 2;
if(a[mid]==x){
return mid;
}else if(a[mid] < x){
l = mid + 1;
}else{
r = mid - 1;
}
}
return -1;
}
int main(){
cout<<findX(a,0,n-1,x); //n为数组长度
}
② 查找第一个大于等于 x 值的序列下标
// 查找第一个大于等于 x 值的序列下标
int findX(int a[],int l,int r,int x){
int mid;
while(l < r){ // 注意< 号
mid = (l+r)/2;
if(a[mid] >= x){ //
r = mid;
}else{
l = mid + 1;
}
}
return l; // 注意return l
}
③ 查找第一个大于 x 值的序列下标
int findX(int a[],int l,int r,int x){
int mid;
while(l<=r){
mid = (l+r)/2;
if(a[mid]<=x){
l = mid + 1;
}else{
r = mid - 1;
}
}
return l;
}
④ 单峰序列
单峰序列是指,在这个序列中存在一个位置,满足这个位置的左侧(含该位置)是严格递增的、右侧(含该位置)是严格递减的,这个位置被称作峰顶位置。现在给定一个单峰序列,求峰顶位置的下标。
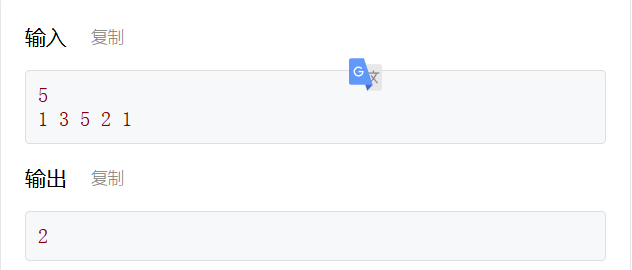
int maxIn = 0;
int mx = 0;
void findX(int a[],int l,int r){
if(l>r)
return ;
int mid = (l+r)/2;
if(a[mid]>mx){
mx = a[mid];
maxIn = mid;
}
findX(a,mid+1,r);
findX(a,l,mid-1);
}
三、双指针
① 两数之和
给定一个严格递增序列A和一个正整数k,在序列A中寻找不同的下标i、j,使得Ai+Aj=k。问有多少对(i,j)同时i<j满足条件。
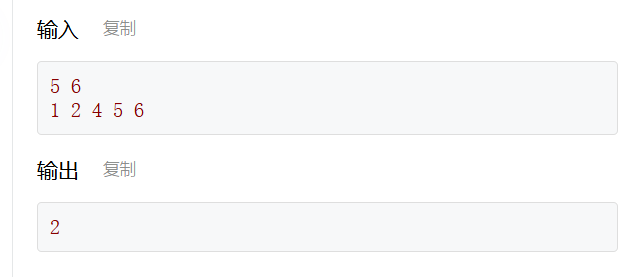
int i=0,j=n-1,cnt=0;
while(i<j){
if(a[i]+a[j]==k){
cnt++;
i++;
j--;
}else if(a[i]+a[j]<k){
i++;
}else{
j--;
}
}
② 序列合并
给定两个升序的正整数序列A和B,将它们合并成一个新的升序序列并输出。
int merge() {
int i = 0, j = 0, counter = 0;
while (i < n && j < m) {
if (a[i] < b[j]) {
mergedNums[counter++] = a[i++];
} else {
mergedNums[counter++] = b[j++];
}
}
while (i < n) {
mergedNums[counter++] = a[i++];
}
while (j < m) {
mergedNums[counter++] = b[j++];
}
return counter;
}
③ 集合求交
给定一个包含 n 个正整数的集合 S1,再给定一个包含 m 个正整数的集合 S2,求两个集合的交集。
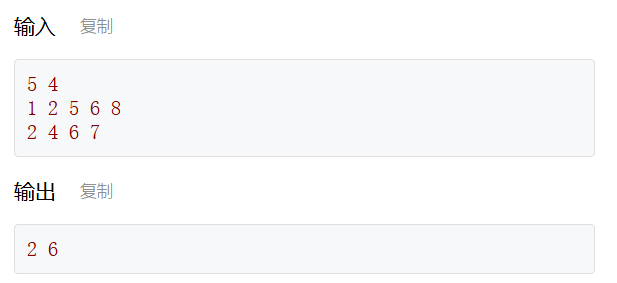
void getIntersection() {
int i = 0, j = 0;
while (i < n && j < m) {
if (a[i] == b[j]) {
intersection.push_back(a[i]);
i++, j++;
} else if (a[i] < b[j]) {
i++;
} else {
j++;
}
}
}
④ 集合求并
给定一个包含 n 个正整数的集合S1,再给定一个包含 m 个正整数的集合S2,求两个集合的并集。
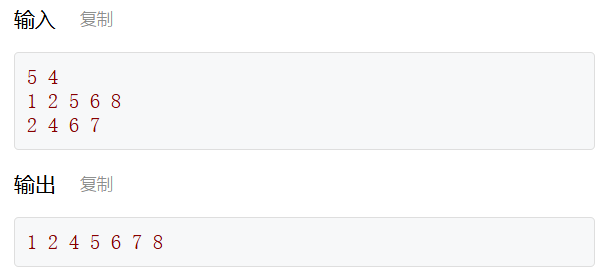
void getUnionSet() {
int i = 0, j = 0;
while (i < n && j < m) {
if (a[i] == b[j]) {
unionSet.push_back(a[i]);
i++, j++;
} else if (a[i] < b[j]) {
unionSet.push_back(a[i++]);
} else {
unionSet.push_back(b[j++]);
}
}
while (i < n) {
unionSet.push_back(a[i++]);
}
while (j < m) {
unionSet.push_back(b[j++]);
}
}
四、其他高效技巧与算法
① 区间和
给定由n个正整数组成的序列A,接下来给出k个查询,每个查询指定两个正整数l、r,计算序列从第l个整数至第r个整数之和,即Al+Al+1+…+Ar。
int main() {
int n;
cin >> n;
vector<int> A(n + 1);
vector<int> prefixSum(n + 1, 0);
// 读取原数组并构建前缀和数组
for (int i = 1; i <= n; ++i) {
cin >> A[i];
prefixSum[i] = prefixSum[i - 1] + A[i];
}
int k;
cin >> k;
for (int i = 0; i < k; ++i) {
int l, r;
cin >> l >> r;
// 计算区间和并输出结果
cout << prefixSum[r] - prefixSum[l - 1] << endl;
}
return 0;
}
② 01 对
给定由n个0或1组成的序列,我们把序列中从左至右(可不连续)存在的0、1称为01对,问在序列中有多少个01对。

int main() {
int n, x, numZero = 0;
scanf("%d", &n);
long long result = 0;
for (int i = 0; i < n; i++) {
scanf("%d", &x);
if (x == 1) {
result += numZero;
} else {
numZero++;
}
}
printf("%lld", result);
return 0;
}
解析:从左到右 01 对,若看 0 ,不确定后面有多少1。但是若看 1,则必知道前面有多少0,这样就知道有多少 01 对了。
③ 左小数
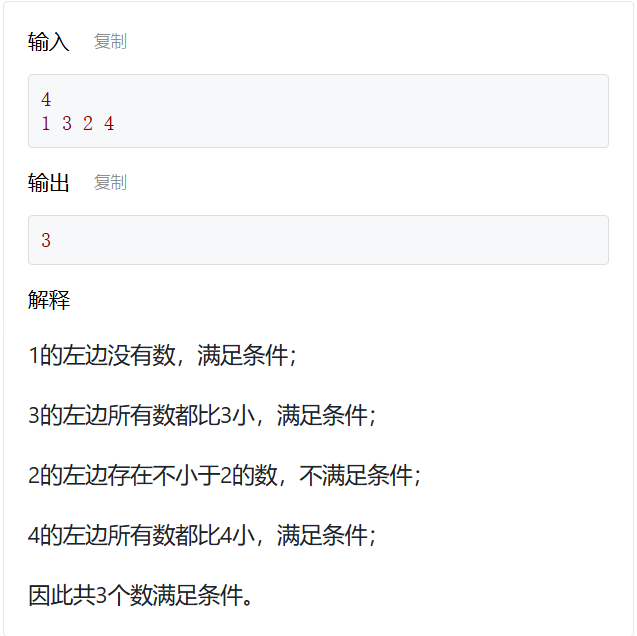
给定由n个正整数组成的序列,问在序列中有多少个数,满足在它左边的所有数都比它小。
int main() {
int n, x, leftMax = 0;
scanf("%d", &n);
int result = 0;
for (int i = 0; i < n; i++) {
scanf("%d", &x);
if (x > leftMax) {
result++;
}
leftMax = max(leftMax, x);
}
printf("%d", result);
return 0;
}
五、数学问题
① 最大公约数
int gcd(int a, int b) {
if (b == 0) {
return a;
} else {
return gcd(b, a % b);
}
}
int main() {
int a, b;
scanf("%d%d", &a, &b);
printf("%d", gcd(a, b));
return 0;
}
② 最小公倍数
int gcd(int a, int b) {
if (b == 0) {
return a;
} else {
return gcd(b, a % b);
}
}
int main() {
int a, b;
scanf("%d%d", &a, &b);
printf("%d", a / gcd(a, b) * b);
return 0;
}
③ 素数
int gcb(int a,int b){
if(b==0){
return a;
}else{
return gcb(b,a%b);
}
}
int main(){
int a,b;
cin>>a>>b;
if(gcb(a,b)==1){
cout<<"Yes";
}else{
cout<<"No";
}
}
补充:打印素数表
void getPrimes(int n) {
memset(isPrime, true, sizeof(isPrime));
for (int i = 2; i <= n; i++) {
if (isPrime[i]) {
primes.push_back(i);
for (int j = i + i; j <= n; j += i) {
isPrime[j] = false;
}
}
}
}
int main() {
int n;
scanf("%d", &n);
getPrimes(n);
for (int i = 0; i < primes.size(); i++) {
printf("%d\n", primes[i]);
}
return 0;
}
④ 质因子
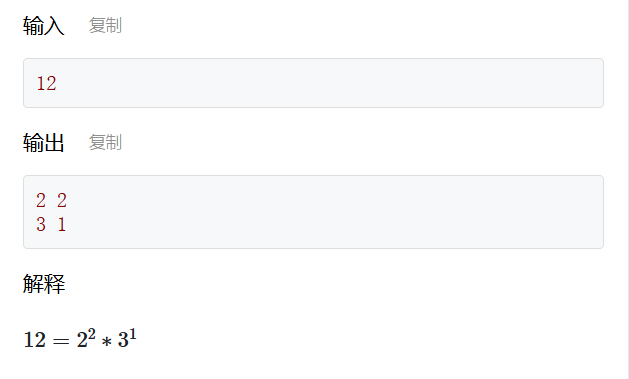
给定一个正整数n,对n进行质因子分解。
void getPrimes(int n) {
memset(isPrime, true, sizeof(isPrime));
for (int i = 2; i <= n; i++) {
if (isPrime[i]) {
primes.push_back(i);
for (int j = i + i; j <= n; j += i) {
isPrime[j] = false;
}
}
}
}
int main() {
int n;
scanf("%d", &n);
getPrimes((int)sqrt(1.0 * n));
for (int i = 0; i < primes.size() && n > 1; i++) {
int counter = 0;
while (n > 1 && n % primes[i] == 0) {
counter++;
n /= primes[i];
}
if (counter > 0) {
printf("%d %d\n", primes[i], counter);
}
}
if (n > 1) {
printf("%d 1", n);
}
return 0;
}
⑤ 组合数
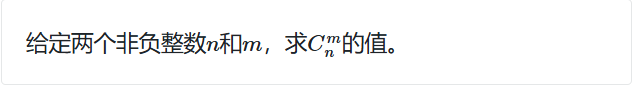
#include <cstdio>
typedef long long LL;
LL C(LL n, LL m) {
LL ans = 1;
for (LL i = 1; i <= m; i++) {
ans = ans * (n - m + i) / i;
}
return ans;
}
int main() {
LL n, m;
scanf("%lld%lld", &n, &m);
printf("%lld", C(n, m));
return 0;
}
六、数据结构
① 栈
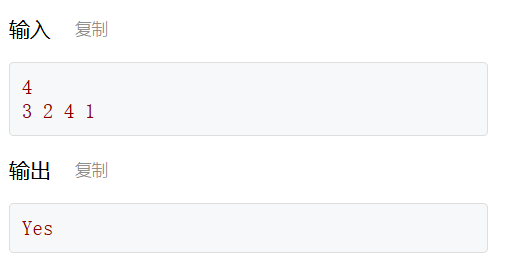
现有一个空栈s和一个正整数n,将1,2,3,…,n依次入栈,期间任意时刻出栈。然后给定一个出栈序列,问其是否是一个合法的出栈序列。
int main() {
int n;
scanf("%d", &n);
stack<int> s;
int x, nowMax = 0;
bool isValid = true;
for (int i = 0; i < n; i++) {
scanf("%d", &x);
if (x > nowMax) {
for (int j = nowMax + 1; j <= x; j++) {
s.push(j);
}
nowMax = x;
}
if (s.top() != x) {
isValid = false;
break;
} else {
s.pop();
}
}
printf(isValid ? "Yes" : "No");
return 0;
}
② 队列
约瑟夫环:假设n个人按编号顺时针从小到大排成一圈(编号为从1到n)。接着约定一个正整数k,从编号为1的人开始顺时针报数(编号为1的人报数1,编号为2的人报数2……),报到k的人离开圈子,然后他的下一个人继续从1开始报数,以此类推,直到圈子里只剩下一个人。
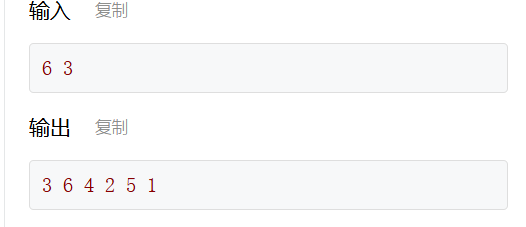
int main(){
int n,k,m;
cin>>n>>m;
queue<int> q;
for(int i=1;i<=n;i++){
q.push(i);
}
int cnt = 0;
while(!q.empty()){
int num = q.front();
cnt++;
if(cnt % m ==0){
cout<<q.front();
q.pop();
if(q.size()>=1){
cout<<" ";
}
}else{
q.pop();
q.push(num);
}
}
}
③ 链表
private:
struct ListNode{
int val;
ListNode* next;
ListNode():val(0),next(NULL){}
ListNode(int val):val(val),next(NULL){}
ListNode(int val,ListNode* next):val(val),next(NULL){}
};
int len;
ListNode* dummyhead; //链表虚拟头结点
public:
MyLinkedList() {
len = 0;
dummyhead = new ListNode();
}
int get(int index) {
if(index<0||index>len-1) return -1;
ListNode* p = dummyhead->next;
while(index--){
p = p ->next;
}
return p->val;
}
void addAtHead(int val) {
ListNode* p = new ListNode(val);
p->next = dummyhead->next;
dummyhead->next = p;
len++;
}
void addAtTail(int val) {
ListNode* p = new ListNode(val),*cur=dummyhead;
while(cur->next) cur = cur->next;
cur->next = p;
len++;
}
void addAtIndex(int index, int val) {
if(index<=0) addAtHead(val);
else if(index==len) addAtTail(val);
else{
ListNode* p = new ListNode(val),*pre = dummyhead;
while(index--) pre = pre->next;
p->next = pre->next;
pre->next = p;
len++;
}
}
void deleteAtIndex(int index) {
if(index<0||index>len-1) return;
ListNode* pre = dummyhead,*p = NULL;
while(index--) pre = pre->next;
p = pre->next;
pre->next = p->next;
delete p;
len--;
}
};
// 创建单链表
ListNode *head = new ListNode,*p = head;
for(int i=1;i<=n;i++){
scanf("%d",&v);
p->next = new ListNode(v);
p = p->next;
}
//头插法
p = q ->next;
q->next = H->next;
H->next = q;
q = p;
//尾插法
LNode *rear = H->next;
while(){
q = new ListNode(v);
rear->next = q;
rear = q;
}
rear->next = NULL;
//单链表法二
struct Node {
int data, next;
} nodes[MAXN];
七、深度优先遍历(DFS)
① 01 串
在一个长度为n的数组中填写0或者1,输出所有可能的结果。
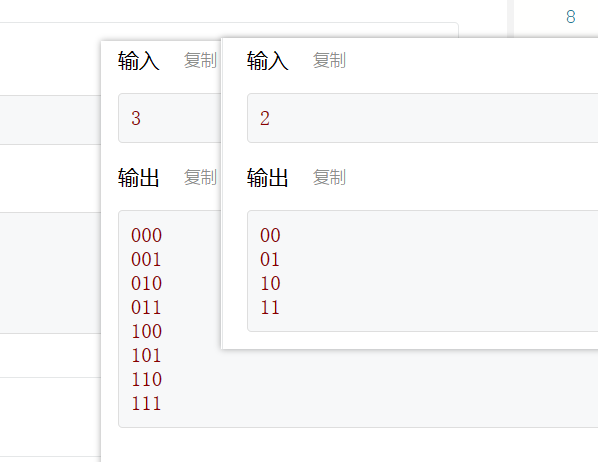
vector<int> temp;
vector<vector<int> > result;
void DFS(int k){
if(k==n) {
result.push_back(temp);
return;
}
temp.push_back(0);
DFS(k+1);
temp.pop_back();
temp.push_back(1);
DFS(k+1);
temp.pop_back();
}
② 子集
给定一个正整数n,假设序列S=[1,2,3,…,n],求S的所有子集。

void DFS(int idx) {
if (idx == n + 1) {
result.push_back(temp);
return;
}
temp.push_back(idx);
DFS(idx + 1);
temp.pop_back();
DFS(idx + 1);
}
bool cmp(vector<int> a, vector<int> b) {
if (a.size() != b.size()) {
return a.size() < b.size();
} else {
return a < b;
}
}
③ 全排列
给定一个正整数n,假设序列S=[1,2,3,…,n],求S的全排列。
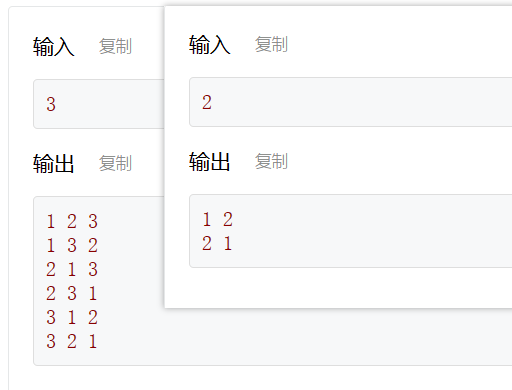
bool used[MAXN] = {false};
void DFS(int idx) {
if (idx == n + 1) {
result.push_back(temp);
return;
}
for (int i = 1; i <= n; i++) {
if (!used[i]) {
temp.push_back(i);
used[i] = true;
DFS(idx + 1);
used[i] = false;
temp.pop_back();
}
}
}
④ 组合
给定两个正整数n、k,假设序列S=[1,2,3,…,n],求从S中任选k个的所有可能结果。
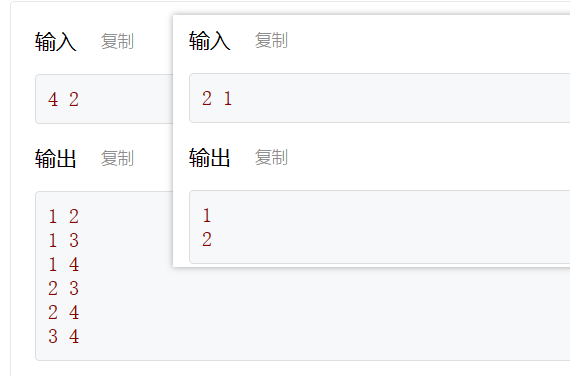
void DFS(int idx) {
if (temp.size() == k) {
result.push_back(temp);
return;
}
if (idx == n + 1) {
return;
}
temp.push_back(idx);
DFS(idx + 1);
temp.pop_back();
DFS(idx + 1);
}
⑤ 有限制的选数Ⅰ
给定n个互不相同的正整数,从中选择若干个数(每个数只能选一次),使得这些数之和为定值K。求满足条件的方案数。
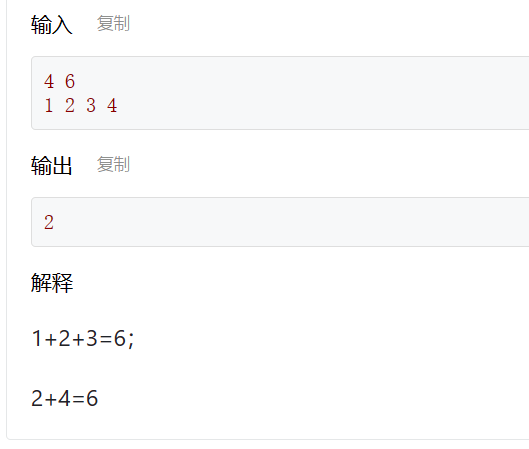
void DFS(int idx, int nowSum) {
if (idx == n + 1) {
if (nowSum == k) {
ans++;
}
return;
}
if (nowSum > k) {
return;
}
DFS(idx + 1, nowSum + a[idx]);
DFS(idx + 1, nowSum);
}
⑥ 有限制的选数Ⅱ
给定n个互不相同的正整数,从中选择若干个数(每个数可以选任意次),使得这些数之和为定值K。求满足条件的方案数。
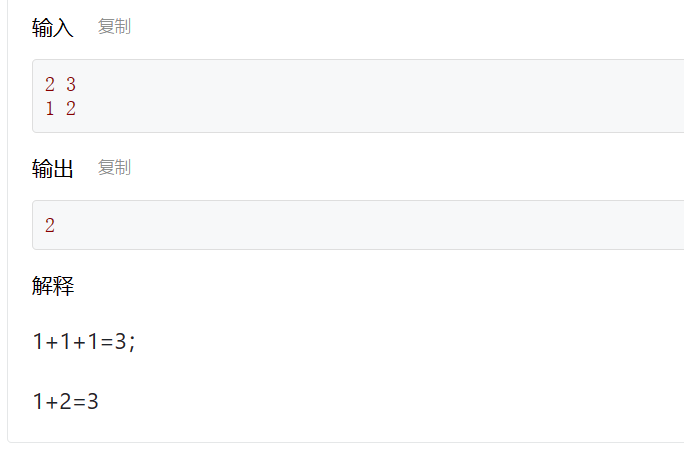
void DFS(int idx, int nowSum) { //k为目标值
if (idx == n + 1) {
if (nowSum == k) {
ans++;
}
return;
}
for (int i = 0; i <= (k - nowSum) / a[idx]; i++) {
DFS(idx + 1, nowSum + i * a[idx]);
}
}
⑦ n皇后
bool vis_col[14],vis_l[30],vis_r[30]; //col 列 ,l左对角线,r右对角线
int n,ans;
void dfs(int row){ //行
if(row==n){
ans++;
return;
}
for(int i=0;i<n;i++){
if(!vis_col[i]&&!vis_l[i-row+n]&&!vis_r[i+row]){
vis_col[i] = vis_l[i-row+n] = vis_r[i+row] = 1;
dfs(row+1);
vis_col[i] = vis_l[i-row+n] = vis_r[i+row] = 0;
}
}
}
⑧ 迷宫可行路径数
现有一个n∗m大小的迷宫,其中1表示不可通过的墙壁,0表示平地。每次移动只能向上下左右移动一格(不允许移动到曾经经过的位置),且只能移动到平地上。求从迷宫左上角到右下角的所有可行路径的条数。

int De[][2] = {{0,1},{0,-1},{1,0},{-1,0}};
int mp[5][5];
bool vis[5][5] = {false};
int cnt = 0;
int n,m;
bool isVilid(int x,int y){
if(x<0||y<0||x>=n||y>=m||vis[x][y]==true||mp[x][y]==1){
return false;
}else{
return true;
}
}
void DFS(int x,int y){
if(x==n-1&&y==m-1){
cnt++;
return;
}
vis[x][y] = true;
for(int i=0;i<5;i++){
int next_x = x + De[i][0];
int next_y = y + De[i][1];
if(isVilid(next_x,next_y)){
DFS(next_x,next_y);
}
}
vis[x][y] = false;
}
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
cin>>mp[i][j];
}
}
DFS(0,0);
cout<<cnt;
}
⑨ 无向连通图的块数
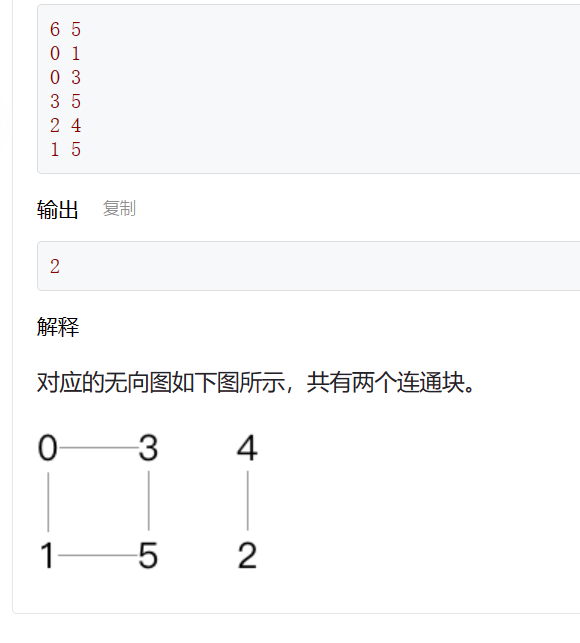
#include <cstdio>
#include <vector>
using namespace std;
const int MAXN = 100;
vector<int> G[MAXN];
bool vis[MAXN];
void DFS(int u) {
vis[u] = true;
for (int i = 0; i < G[u].size(); i++) {
int v = G[u][i];
if (!vis[v]) {
DFS(v);
}
}
}
int main() {
memset(vis, false, sizeof(vis));
int n, m, u, v;
scanf("%d%d", &n, &m);
for (int i = 0; i < m; i++) {
scanf("%d%d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
int blockCount = 0;
for (int i = 0; i < n; i++) {
if (!vis[i]) {
DFS(i);
blockCount++;
}
}
printf("%d", blockCount);
return 0;
}
八、广度优先搜索(BFS)
① 数字操作
从整数1开始,每轮操作可以选择将上轮结果加1或乘2。问至少需要多少轮操作才能达到指定整数 n。
const int MAXN = 100000;
bool inQueue[MAXN + 1] = {false};
int getStep(int n) {
int step = 0;
queue<int> q;
q.push(1);
while (true) {
int cnt = q.size();
for (int i = 0; i < cnt; i++) {
int front = q.front();
q.pop();
if (front == n) {
return step;
}
inQueue[front] = true;
if (front * 2 <= n && !inQueue[front * 2]) {
q.push(front * 2);
}
if (front + 1 <= n && !inQueue[front + 1]) {
q.push(front + 1);
}
}
step++;
}
}
② 矩阵中的块
现有一个n∗m的矩阵,矩阵中的元素为0或1。然后进行如下定义:
- 位置(x,y)与其上下左右四个位置(x,y+1)、(x,y−1)、(x+1,y)、(x−1,y)是相邻的;
- 如果位置(x1,y1)与位置(x2,y2)相邻,且位置(x2,y2)与位置(x3,y3)相邻,那么称位置(x1,y1)与位置(x3,y3)也相邻;
- 称个数尽可能多的相邻的
1构成一个“块”。
求给定的矩阵中“块”的个数。
int n, m, matrix[MAXN][MAXN];
bool inQueue[MAXN][MAXN] = {false};
const int MAXD = 4;
int dx[MAXD] = {0, 0, 1, -1};
int dy[MAXD] = {1, -1, 0, 0};
bool canVisit(int x, int y) {
return x >= 0 && x < n && y >= 0 && y < m && matrix[x][y] == 1 && !inQueue[x][y];
}
void BFS(int x, int y) {
queue<Position> q;
q.push(Position(x, y));
inQueue[x][y] = true;
while (!q.empty()) {
Position front = q.front();
q.pop();
for (int i = 0; i < MAXD; i++) {
int nextX = front.first + dx[i];
int nextY = front.second + dy[i];
if (canVisit(nextX, nextY)) {
inQueue[nextX][nextY] = true;
q.push(Position(nextX, nextY));
}
}
}
}
③ 迷宫最短步数
现有一个n∗m大小的迷宫,其中1表示不可通过的墙壁,0表示平地。每次移动只能向上下左右移动一格,且只能移动到平地上。求从迷宫左上角到右下角的最小步数。
bool canVisit(int x, int y) {
return x >= 0 && x < n && y >= 0 && y < m && maze[x][y] == 0 && !inQueue[x][y];
}
int BFS(int x, int y) {
queue<Position> q;
q.push(Position(x, y));
inQueue[x][y] = true;
int step = 0;
while (!q.empty()) {
int cnt = q.size();
while (cnt--) {
Position front = q.front();
q.pop();
if (front.first == n - 1 && front.second == m - 1) {
return step;
}
for (int i = 0; i < MAXD; i++) {
int nextX = front.first + dx[i];
int nextY = front.second + dy[i];
if (canVisit(nextX, nextY)) {
inQueue[nextX][nextY] = true;
q.push(Position(nextX, nextY));
}
}
}
step++;
}
return -1;
}
④ 迷宫最短路径
现有一个n∗m大小的迷宫,其中1表示不可通过的墙壁,0表示平地。每次移动只能向上下左右移动一格,且只能移动到平地上。假设左上角坐标是(1,1),行数增加的方向为x增长的方向,列数增加的方向为y增长的方向,求从迷宫左上角到右下角的最少步数的路径。
typedef pair<int, int> Position;
const int MAXN = 100;
int n, m, maze[MAXN][MAXN];
bool inQueue[MAXN][MAXN] = {false};
Position pre[MAXN][MAXN];
const int MAXD = 4;
int dx[MAXD] = {0, 0, 1, -1};
int dy[MAXD] = {1, -1, 0, 0};
bool canVisit(int x, int y) {
return x >= 0 && x < n && y >= 0 && y < m && maze[x][y] == 0 && !inQueue[x][y];
}
void BFS(int x, int y) {
queue<Position> q;
q.push(Position(x, y));
inQueue[x][y] = true;
while (!q.empty()) {
Position front = q.front();
q.pop();
if (front.first == n - 1 && front.second == m - 1) {
return;
}
for (int i = 0; i < MAXD; i++) {
int nextX = front.first + dx[i];
int nextY = front.second + dy[i];
if (canVisit(nextX, nextY)) {
pre[nextX][nextY] = Position(front.first, front.second);
inQueue[nextX][nextY] = true;
q.push(Position(nextX, nextY));
}
}
}
}
void printPath(Position p) {
Position prePosition = pre[p.first][p.second];
if (prePosition == Position(-1, -1)) {
printf("%d %d\n", p.first + 1, p.second + 1);
return;
}
printPath(prePosition);
printf("%d %d\n", p.first + 1, p.second + 1);
}






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








