NLP学习日记二：HMM-witerbi算法

开干：从当前，计算未来可能状态的概率，并求最大的，同时输出所走的路径（中间过程）

比如你现在到你家的概率最大，是怎么得出的？中间经过了哪里？你到家之后开始回想走过的路径

一：引入：

1. 一句话总结

Viterbi算法就是“隐马尔可夫模型（HMM）中的最强侦探”——它通过观察到的线索（观测序列），反向推理出最有可能的隐藏状态序列。

---

2. 生活化类比

想象你是一个医生，通过病人的症状（观测值）推测他每天的健康状态（隐藏状态）：

• 已知：

  • 病人3天的症状：正常 → 感冒 → 头晕

  • 两种可能的隐藏状态：健康 或 发烧

  • 状态之间的转移概率（比如“健康”第二天变“发烧”的概率是30%）

  • 每种状态产生症状的概率（比如“发烧”时“头晕”的概率是60%）

• 目标：
  找出这3天最可能的真实状态组合，比如 健康 → 健康 → 发烧。

---

3. 算法核心思想

• 每一步只保留最优解：
  像走迷宫时，每到岔路口只选一条最优路径，扔掉其他可能性，避免组合爆炸。

• 动态规划：
  用表格记录每一步每个状态的最大概率，最后回溯找出全局最优路径。

---

4. 具体步骤（结合例子）

步骤1：初始化

• 问题：第一天症状是“正常”，病人可能是“健康”还是“发烧”？

• 计算：

  • 如果第一天是“健康”：
    概率 = 初始健康概率（60%）× 健康时“正常”的概率（50%） = 0.3

  • 如果第一天是“发烧”：
    概率 = 初始发烧概率（40%）× 发烧时“正常”的概率（10%） = 0.04

• 结果：
  更可能是“健康”（0.3 > 0.04），记录下这个概率和路径。

步骤2：递推（第二天）

• 问题：第二天症状是“感冒”，病人可能的状态路径有哪些？

• 计算（以“健康”为例）：

  • 前一天是“健康” → 今天仍“健康”：
    概率 = 前一天的0.3 × 健康保持健康的概率（70%）× 健康时“感冒”的概率（40%） = 0.084

  • 前一天是“发烧” → 今天变“健康”：
    概率 = 前一天的0.04 × 发烧变健康的概率（40%）× 健康时“感冒”的概率（40%） = 0.0064

• 选择：
  保留最大值 0.084（路径：健康 → 健康），丢弃其他路径。

步骤3：终止（第三天）

• 问题：第三天症状是“头晕”，最终状态的概率如何？

• 计算（以“发烧”为例）：

  • 前一天是“健康” → 今天变“发烧”：
    概率 = 0.084 × 健康变发烧的概率（30%）× 发烧时“头晕”的概率（60%） = 0.01512

  • 前一天是“发烧” → 今天仍“发烧”：
    概率 = 0.027 × 发烧保持发烧的概率（60%）× 发烧时“头晕”的概率（60%） = 0.00972

• 选择：
  最大值 0.01512（路径：健康 → 健康 → 发烧）。

步骤4：回溯

从最后一天的最高概率状态（“发烧”）倒推：

• 第三天“发烧”来自第二天的“健康”

• 第二天“健康”来自第一天的“健康”

• 最终路径：健康 → 健康 → 发烧

---

5. 为什么高效？

• 剪枝（Pruning）：
  每一步只保留到当前状态的最优路径，扔掉其他可能性。
  （比如第二天计算“健康”时，直接丢弃了“发烧→健康”的低概率路径）

• 复杂度从指数级降到平方级：
  如果暴力穷举所有路径需要计算 23=823=8 种组合，而Viterbi只需 3×22=123×22=12 次计算。

---

6. 应用场景

• 语音识别：
  观测值=声音信号 → 隐藏状态=单词或音素

• 自然语言处理：
  观测值=句子中的词 → 隐藏状态=词性（名词/动词等）

• 生物基因分析：
  观测值=DNA碱基序列 → 隐藏状态=基因编码区/非编码区

---

7. 通俗总结

Viterbi算法就是：

1. “看症状猜病情”：通过可见的表现，反推隐藏的真实状态。

2. “每一步只记最优解”：像做选择题，每个步骤只保留最高分的选项。

3. “倒着往回找”：从最后一步的最高分答案，反向推出完整路径。

一句话：

“它用动态规划的思路，高效地找出HMM中最可能的隐藏状态序列，避免穷举所有可能性。”

############################################################################# 

二：【 接下来是真正的算法讲解 】

注意：括号里面解释暂且不管，是后面代码示例

先看看书本讲的：

 

 将A转移概率,B发射概率带入，得到：

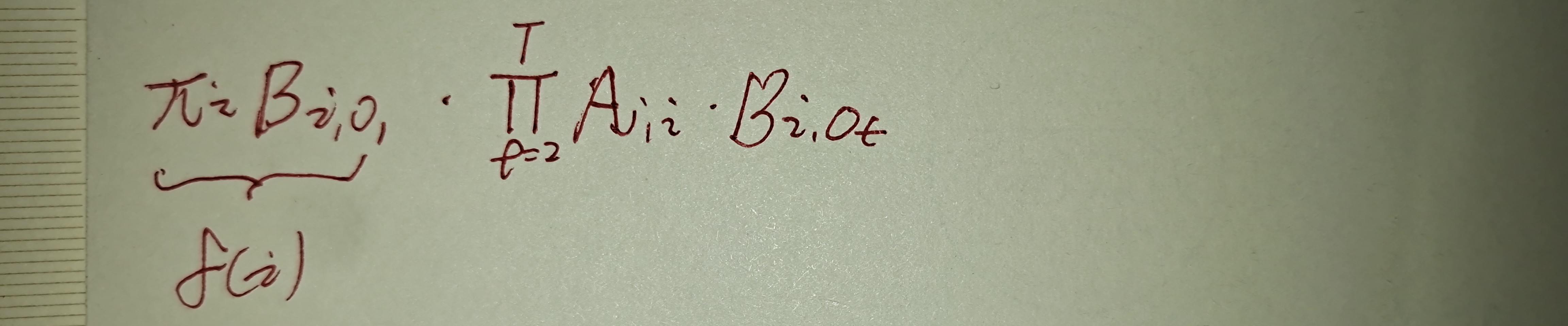
 也即下图形式公式（严格），且有矩阵运算：t,j *j.i, *i,o 得到 t*o维度的矩阵。

1. 变量定义

• 状态集合：Q={q1,q2,...,qN}（如：Healthy, Fever）

• 观测序列：O=(o1,o2,...,oT)（如：normal, cold, dizzy）

• 模型参数：qi 就是Si(状态）qi at t=1 就是在t = 1的状态

  • 初始概率：πi=P(qi at t=1)（代码中 start_p）

  • 转移概率：aij=P(qj at t+1∣qi at t)（代码中 trans_p）

  • 发射概率：bi(ot)=P(ot∣qi)（代码中 emit_p）

  • δt​,i :t时刻以qi(或Si)结尾的所有局部路径的最大概率

  • ψt,i:存储局部最优路径末状态的前驱状态

 整个算法我们只关注：δt​,i  和 ψt,i，即 最大概率 和 最优路径

---

2. Viterbi算法公式

(1) 初始化（t=1）

δ1(i)=πi⋅bi(o1), 

对所有状态  i∈Q δ1​(i)=πi​⋅bi​(o1​),

对所有状态  i∈Q ψ1(i)=0 （没有前驱，为0）

• 物理意义：在第一个时间步，状态 i 的概率由初始概率和发射概率直接决定。

(2) 递推（t=2t=2 到 t=Tt=T）

δt(j)=max⁡ 1≤i≤N [δt−1(i)⋅aij]⋅bj(ot),

对所有状态 j∈Q δt​(j)=1≤i≤N max​[δt−1​(i)⋅aij​]⋅bj​(ot​),

对所有状态 j∈Q ψt(j)=arg⁡max⁡ 1≤i≤N [ δt−1(i)⋅aij ]   

• 物理意义：

  • δt(j)：到时间 tt 时状态 jj 的最大概率路径的概率。

  • ψt(j) ：该路径的前一个最优状态（用于回溯）。

(3) 终止（t=T）

P∗=max⁡ 1≤i≤NδT(i) 

qT∗=arg⁡max⁡ 1≤i≤NδT(i) 

• 物理意义：

  • P∗：最优路径的全局概率。

  • qT∗：最终时间步的最优状态。

(4) 回溯（t=T−1 到 t=1）

qt∗=ψt+1(qt+1∗)

• 物理意义：从 qT∗开始，逆序回溯所有最优状态。

 例子：

1. 问题定义（公式与代码对应）

HMM参数（与代码输入一致）：

states = ('Healthy', 'Fever')                          # 隐藏状态集合
observations = ('normal', 'cold', 'dizzy')             # 观测序列
start_p = {'Healthy': 0.6, 'Fever': 0.4}              # 初始概率 π
trans_p = {                                           # 转移矩阵 A
    'Healthy': {'Healthy': 0.7, 'Fever': 0.3},
    'Fever': {'Healthy': 0.4, 'Fever': 0.6}
}
emit_p = {                                            # 发射矩阵 B
    'Healthy': {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
    'Fever': {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6}
}

---

2. Viterbi算法公式分步解析

公式1：初始化（t=1）

δ1(i)=πi⋅bi(o1)

对应代码：

# 初始化Viterbi矩阵V和路径path
V = [{}]  # V[t][y]表示t时刻状态y的最大概率
path = {} # 记录路径

# 初始化第一个时间步（t=0，对应公式t=1）
for y in states:
    V[0][y] = start_p[y] * emit_p[y][obs[0]]  # δ₁(i) = π_i * b_i(o₁)
    path[y] = [y]  # 初始路径

计算过程：

• Healthy: 0.6×0.5=0.3

• Fever: 0.4×0.1=0.04

---

公式2：递推（t>1）

δt(j)=max⁡1≤i≤N [δt−1(i)⋅aij]⋅bj(ot)

for t in range(1, len(obs)):
    V.append({})
    newpath = {}
    
    for y in states:
        # 计算max(δ_{t-1}(i) * a_{ij}) * b_j(o_t)
        (prob, state) = max(
            [(V[t-1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) 
            for y0 in states
        )
        V[t][y] = prob  # 存储δ_t(j)
        newpath[y] = path[state] + [y]  # 更新路径
    
    path = newpath  # 剪枝：只保留最优路径

计算过程（t=1→t=2）：

• δ2(Healthy)=max⁡(0.3×0.7×0.4, 0.04×0.4×0.4)=0.084（来自Healthy）

• δ2(Fever)=max⁡(0.3×0.3×0.3, 0.04×0.6×0.3)=0.027（来自Healthy）

---

公式3：终止

P∗=max⁡1≤i≤NδT(i)

qT∗=arg⁡max⁡1≤i≤NδT(i)

对应代码：

n = len(obs) - 1
(prob, state) = max([(V[n][y], y) for y in states])  # 找最终最大概率和状态

计算过程（t=3）：

• δ3(Healthy)=max⁡(0.084×0.7×0.1, 0.027×0.4×0.1)=0.00588

• δ3(Fever)=max⁡(0.084×0.3×0.6, 0.027×0.6×0.6)=0.01512

• 最优：P∗=0.01512, qT∗=Fever

---

公式4：路径回溯

qt∗=ψt+1(qt+1∗)

对应代码：

return (prob, path[state])  # 返回最优概率和路径

回溯路径：

• 终点：Fever ← 来自Healthy (t=2) ← Healthy (t=1)

---

3. 完整计算过程表格

时间步	Healthy (δ)	Fever (δ)	最优前驱
t₁	0.3	0.04	-
t₂	0.084 (H→H)	0.027 (H→F)	Healthy → Healthy
t₃	0.00588	0.01512	Healthy → Fever

---

4. 关键点总结

1. 动态规划本质：每个状态仅保留最大概率路径（剪枝）。

2. 时间复杂度：O(T×N²)（N=状态数，T=时间步）。

3. 代码对应：

   • V[t][y] 存储 δt(y)δt​(y)

   • path 通过字典回溯最优序列

完整代码：

import numpy as np

def viterbi(obs, states, start_p, trans_p, emit_p):
    """
    HMM Viterbi算法实现
    
    参数:
    obs: 观察序列 (list或1D数组)
    states: 隐藏状态集合 (list)
    start_p: 初始概率 (dict或1D数组)
    trans_p: 转移概率矩阵 (dict或2D数组)
    emit_p: 发射概率矩阵 (dict或2D数组)
    
    返回:
    最优路径概率, 最优路径
    """
    V = [{}]  # 初始化Viterbi矩阵
    path = {}  # 初始化路径
    
    # 初始化第一个观测节点
    for y in states:
        V[0][y] = start_p[y] * emit_p[y][obs[0]]
        path[y] = [y]
    
    # 对剩下的观测节点进行迭代
    for t in range(1, len(obs)):
        V.append({})
        newpath = {}
        
        for y in states:
            # 计算到当前状态的最大概率和对应的前一个状态
            (prob, state) = max(
                [(V[t-1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) 
                 for y0 in states]
            )
            V[t][y] = prob
            newpath[y] = path[state] + [y]
        
        path = newpath
    
    # 找出最后一个时间步的最大概率和对应路径
    n = len(obs) - 1
    (prob, state) = max([(V[n][y], y) for y in states])
    
    return (prob, path[state])

# 示例用法
if __name__ == "__main__":
    # 隐藏状态
    states = ('Healthy', 'Fever')
    
    # 观察序列
    observations = ('normal', 'cold', 'dizzy')
    
    # 初始概率
    start_probability = {'Healthy': 0.6, 'Fever': 0.4}
    
    # 转移概率
    transition_probability = {
        'Healthy': {'Healthy': 0.7, 'Fever': 0.3},
        'Fever': {'Healthy': 0.4, 'Fever': 0.6}
    }
    
    # 发射概率
    emission_probability = {
        'Healthy': {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
        'Fever': {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6}
    }
    
    # 运行Viterbi算法
    prob, path = viterbi(observations, 
                        states, 
                        start_probability, 
                        transition_probability, 
                        emission_probability)
    
    print(f"最优路径概率: {prob:.6f}")
    print("最优隐藏状态路径:", ' -> '.join(path))

 计算矩阵：

初始概率：
H₀ = 0.6 * 0.5 = 0.3
F₀ = 0.4 * 0.1 = 0.04

t₁ → t₂转移：
H₁ = max(0.3*0.7*0.4, 0.04*0.4*0.4) = max(0.084, 0.0064) = 0.084 (来自H)
F₁ = max(0.3*0.3*0.3, 0.04*0.6*0.3) = max(0.027, 0.0072) = 0.027 (来自H)

t₂ → t₃转移：
H₂ = max(0.084*0.7*0.1, 0.027*0.4*0.1) = max(0.00588, 0.00108) = 0.00588 (来自H)
F₂ = max(0.084*0.3*0.6, 0.027*0.6*0.6) = max(0.01512, 0.00972) = 0.01512 (来自H)

时间步       t₀ (初始)          t₁ (normal)          t₂ (cold)            t₃ (dizzy)
状态        
Healthy    开始               H₀=0.3               H₁=0.084            H₂=0.00588
             │                 │   ↘                 │   ↘                │
             ▼                 ▼      ↘              ▼      ↘             ▼
Fever      ——————           F₀=0.04 ————→ F₁=0.027 ————→ F₂=0.01512 (最优)

终点：F₂ (0.01512)  
回溯路径：F₂ ← H₁ ← H₀  
最终序列：[Healthy, Healthy, Fever]