数据结构与算法基础-(4)，音视频开发需要哪些知识

最新推荐文章于 2024-11-10 20:00:00 发布

2401_84181383

最新推荐文章于 2024-11-10 20:00:00 发布

阅读量621

点赞数 27

分类专栏：程序员文章标签：音视频

本文链接：https://blog.csdn.net/2401_84181383/article/details/137731438

版权

程序员专栏收录该内容

29 篇文章 0 订阅

订阅专栏

自我介绍一下，小编13年上海交大毕业，曾经在小公司待过，也去过华为、OPPO等大厂，18年进入阿里一直到现在。

深知大多数HarmonyOS鸿蒙开发工程师，想要提升技能，往往是自己摸索成长或者是报班学习，但对于培训机构动则几千的学费，着实压力不小。自己不成体系的自学效果低效又漫长，而且极易碰到天花板技术停滞不前！

因此收集整理了一份《2024年HarmonyOS鸿蒙开发全套学习资料》，初衷也很简单，就是希望能够帮助到想自学提升又不知道该从何学起的朋友，同时减轻大家的负担。

htt

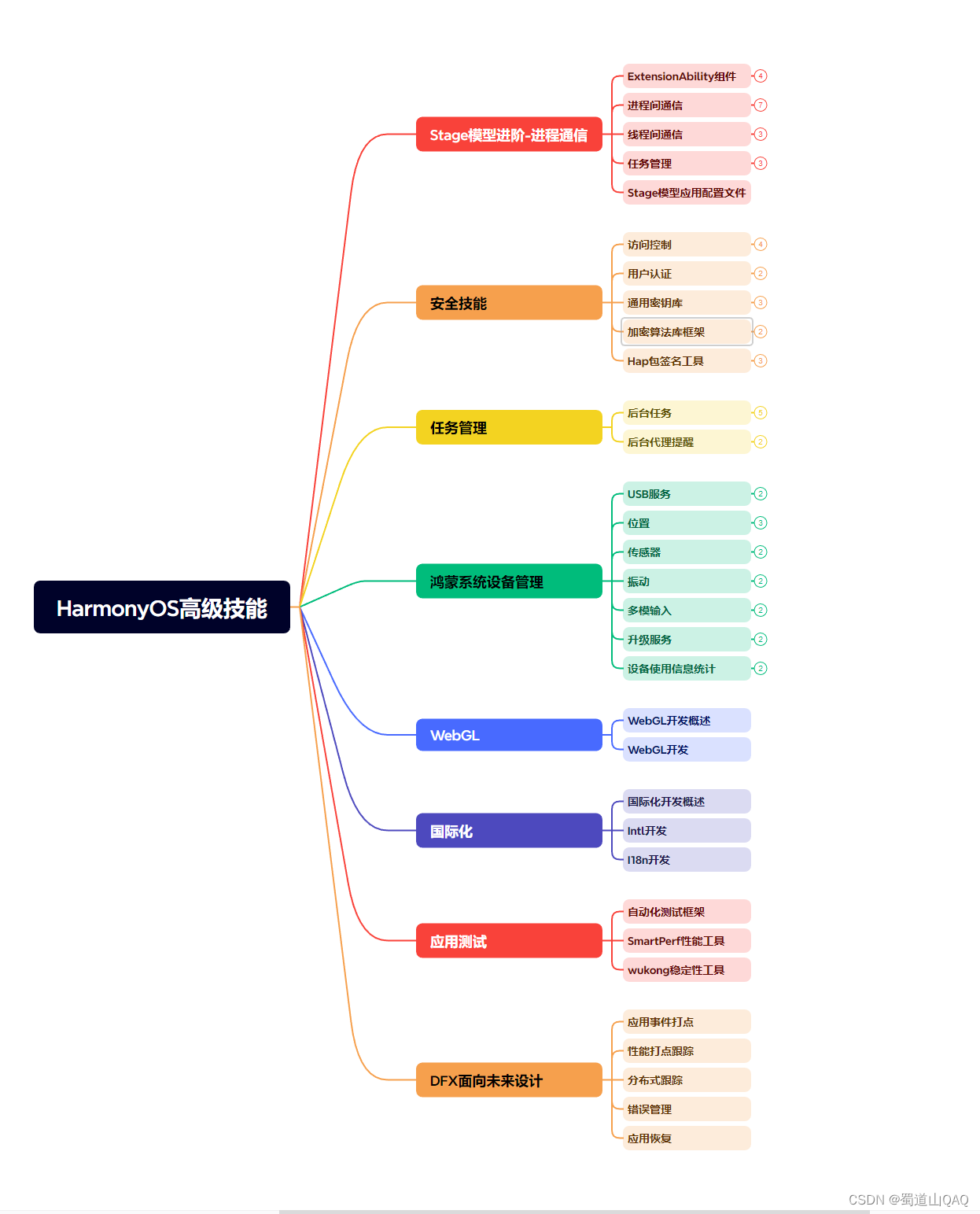
既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，基本涵盖了95%以上HarmonyOS鸿蒙开发知识点，真正体系化！

由于文件比较大，这里只是将部分目录大纲截图出来，每个节点里面都包含大厂面经、学习笔记、源码讲义、实战项目、讲解视频，并且会持续更新

如果你觉得这些内容对你有帮助，可以添加VX：vip204888 （备注鸿蒙获取）

一个人可以走的很快，但一群人才能走的更远。不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎扫码加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

" 栈 " 的操作 🍬

Stack( ) : 创建一个空栈, 不包含任何数据

push (item) : 将 item 加入栈顶 , 无返回值

pop ( ) : 将栈顶数据项移除, 并返回, 被修改

peak ( ) : “窥视” 栈顶数据项, 返回栈顶的数据项但不移除, 栈不被修改.

isEmpty ( ) : 返回栈是否为空栈

size ( ) : 返回栈中有多少个数据项

考点1:

用Python实现ADT Stack🧁

注意细节: Stack 的两端对应list设置

可以将 List 的任意一端 ( index = 0 或者 - 1 ) —>设置为栈

我们选用 List 的末端 ( index = -1 ) 作为栈顶

这样栈的操作就可以通过对 list 的append 和 pop 来实现~

python中的赋值语句🍩

if语句，当条件成立时运行语句块。经常与else, elif（相当于else if）配合使用。
for语句，遍列列表、字符串、字典、集合等迭代器，依次处理迭代器中的每个元素。
while语句，当条件为真时，循环运行语句块。
try语句。与except, finally, else配合使用处理在程序运行中出现的异常情况。
class语句。用于定义类型。
def语句。用于定义函数和类型的方法。
pass语句。表示此行为空，不运行任何操作。
assert语句。用于程序调适阶段时测试运行条件是否满足。
with语句。Python2.6以后定义的语法，在一个场景中运行语句块。比如，运行语句块前加锁，然后在语句块运行退出后释放锁。
yield语句。在迭代器函数内使用，用于返回一个元素。
raise语句。抛出一个异常。
import语句。导入一个模块或包。常用写法：from module import name, import module as name, from module import name as anothername

时间复杂度基本单位是: 赋值语句

左为栈顶,时间复杂度为O(n) 🍨

#左边为顶,右边为低
class Stack:
    def \_\_init\_\_(self):
        self.items = []

    def isEmpty(self):
        return self.items == []

    def push(self,item):
        self.items.insert(0,item)

    def pop(self):
        return self.items.pop(0)

    def peek(self):
        return self.items[0]

    def size(self):
        return len(self.items)

时间复杂度基本单位是: 赋值语句

当左边为栈顶时,当我们往里面加入(pop)元素时,我们会发现后面的每个元素都会向后移一位,就像是排队的时候有个人突然插在前面,后面的人不得不向后退一位,他们等待的时间就会更长.如果有n个元素就会移动n位,所以当左边作为栈顶时,这个****栈的时间复杂度是O(n).

以下是左边作为栈顶时插入元素的示意图

右为栈顶,时间复杂度O(1) 🍧

# 左边为低,右边为顶--->更高效
class Stack:#Stack---->ADT
    def \_\_init\_\_(self):
        self.items =[]

    def isEmpty(self):
        return self.items == []

# 满足这些属性(行为)的是栈
    def push(self,item):
        self.items.append(item)

    def pop(self):
        return self.items.pop()

    def peek(self):
        return self.items[len(self.items)-1]

    #
    def size(self):
        return len(self.items)

s = Stack()