最全进阶C语言——数据的存储【详解】，2024年最新2024大数据开发目前最稳定和高效的UI适配方案

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化资料的朋友，可以戳这里获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

//11111111111111111111111111110110 - -10的补码
//FFFFFFF6

return 0;

}

![在这里插入图片描述](https://img-blog.csdnimg.cn/d1e582fef72c4c32bf5087b7af8fed24.png)  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/be90d242ee624f00add9bbfdcc3fca93.png)


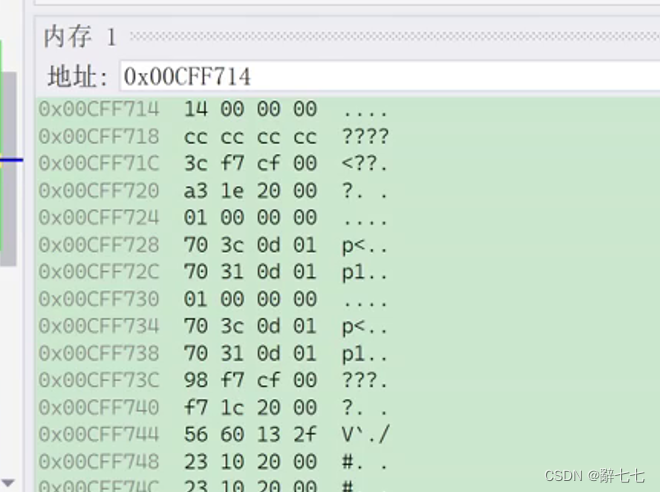
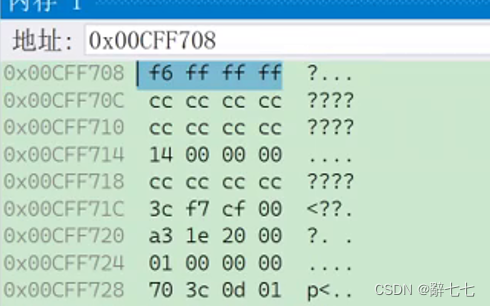
调试后我们可以看到对于a和b分别存储的是补码。但是我们发现顺序有点不对劲。  
 这是又为什么？


### 2.2 大小端介绍


**什么大端小端：**



> 
> 大端（存储）模式，是指数据的低位保存在内存的高地址中，而数据的高位，保存在内存的低地址中；  
>  小端（存储）模式，是指数据的低位保存在内存的低地址中，而数据的高位,，保存在内存的高地址中
> 
> 
> 


画图演示：  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/02c521ed01e8437ca7534ce7c2e90cf9.png)


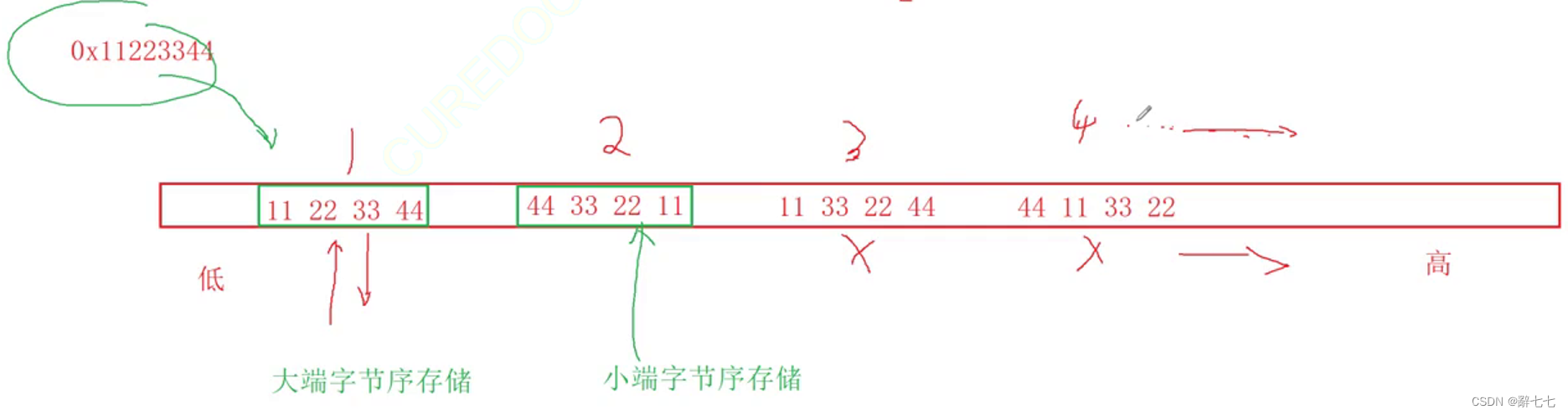
**为什么有大端和小端：**



> 
> 为什么会有大小端模式之分呢？这是因为在计算机系统中，我们是以字节为单位的，每个地址单元 都对应着一个字节，一个字节为8 bit。但是在C语言中除了8 bit的char之外，还有16 bit的short 型，32 bit的long型（要看具体的编译器），另外，对于位数大于8位的处理器，例如16位或者32位的处理器，由于寄存器宽度大于一个字节，那么必然存在着一个如何将多个字节安排的问题。因 此就导致了大端存储模式和小端存储模式。  
>  例如：一个 16bit 的 short 型 x ，在内存中的地址为 0x0010 ， x 的值为 0x1122 ，那么 0x11 为 高字节， 0x22为低字节。对于大端模式，就将 0x11 放在低地址中，即 0x0010 中， 0x22 放在高 地址中，即 0x0011中。小端模式，刚好相反。我们常用的 X86 结构是小端模式，而 KEIL C51 则为大端模式。很多的ARM，DSP都为小端模式。有些ARM处理器还可以由硬件来选择是大端模式 还是小端模式
> 
> 
> 


百度2015年系统工程师笔试题：



> 
> 请简述大端字节序和小端字节序的概念，设计一个小程序来判断当前机器的字节序。
> 
> 
> 

//如果是大端返回0
//如果是小端返回1
#include <stdio.h>
int check_sys()
{
int i = 1;
return (*(char*)&i);
}
int main()
{
int ret = check_sys();
if (ret == 1)
{
printf(“小端\n”);
}
else
{
printf(“大端\n”);
}
return 0;
}

运行结果：  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/cd4c40782a6b4372ab581603b67e4f9d.png)


### 2.3 练习


**练习1**

//1.输出什么？
#include <stdio.h>
int main()
{
char a = -1;
//10000000000000000000000000000001 原码
//11111111111111111111111111111110 反码
//11111111111111111111111111111111 补码
//11111111 - 截断
//整型提升
//11111111111111111111111111111111
//11111111111111111111111111111110
//10000000000000000000000000000001 -1
signed char b = -1;
//signed char与 char结果一样
unsigned char c = -1;
//11111111 - 截断
//00000000000000000000000011111111无符号数高位直接补零
printf(“a=%d,b=%d,c=%d”, a, b, c);
return 0;
}

char的二进制序列计算  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/4cefa98389ed48e483ba72ace6c11c80.png)  
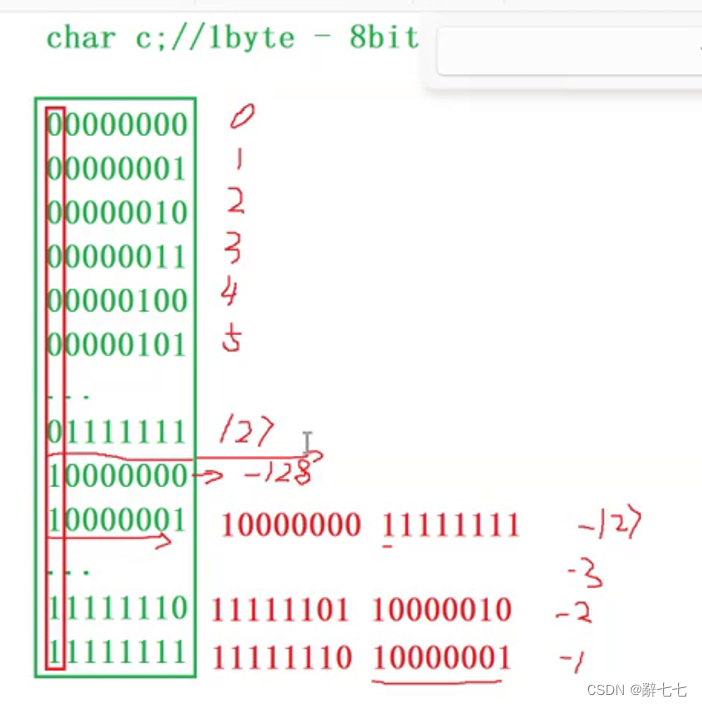
 有符号char的取值范围是 （-128~127）  
 无符号char的取值范围是 （0~255）  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/e8bc912576b44d30a20b97e5482cafee.png)  
 **%d与%u的输出结果**

#include <stdio.h>
int main()
{
unsigned int num = -10;
//10000000000000000000000000001010 原码
//11111111111111111111111111110101 反码
//11111111111111111111111111110110 补码
//无符号数原码补码相同
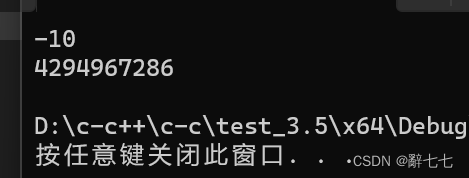
printf(“%d\n”, num);
printf(“%u\n”, num);

return 0;

}

![在这里插入图片描述](https://img-blog.csdnimg.cn/0e902cf074ff431980435252c7a862c2.png)


![在这里插入图片描述](https://img-blog.csdnimg.cn/8d8049acc81e4a69b2e957e1b61e4aad.png)  
 **练习2**

#include <stdio.h>
int main()
{
char a = -128;
printf(“%u\n”, a);
return 0;
}

![在这里插入图片描述](https://img-blog.csdnimg.cn/0ff0a139ad1b40cea75b0f79530c7aae.png)  
 **练习3**

#include <stdio.h>
int main()
{
char a = 128;
printf(“%u\n”, a);
return 0;
}

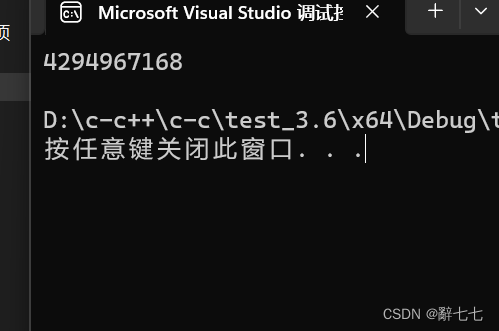
运算过程与练习2的过程相似  
 运行结果  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/5989fee13b9c4f11add9f0a126b2e13a.png)  
 **练习4**

#include <stdio.h>
int main()
{
int i = -20;
unsigned int j = 10;
//10000000 00000000 00000000 00010100
//11111111 11111111 11111111 11101011
//11111111 11111111 11111111 11101100 - (-20)补码
//00000000 00000000 00000000 00001010 - (10)原码
//11111111 11111111 11111111 11110110 - (i+j)结果，计算机的结果，是存在内存中，是补码
//10000000 00000000 00000000 00001010 - 补码变成原码
//计算结果 -10
printf(“%d\n”, i + j);
return 0;
}

**练习5**

#include <stdio.h>
#include <windows.h>
int main()
{
unsigned int i;
for (i = 9; i >= 0; i–)
{
printf(“%u\n”, i);
Sleep(1000);//单位是毫秒
}
return 0;
}

打印结果：  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/142bdeb7e97146f58226ff18bcb6f8c7.png)



> 
> Sleep(1000)用来降低打印速度的头文件为#include <windows.h>
> 
> 
> 



> 
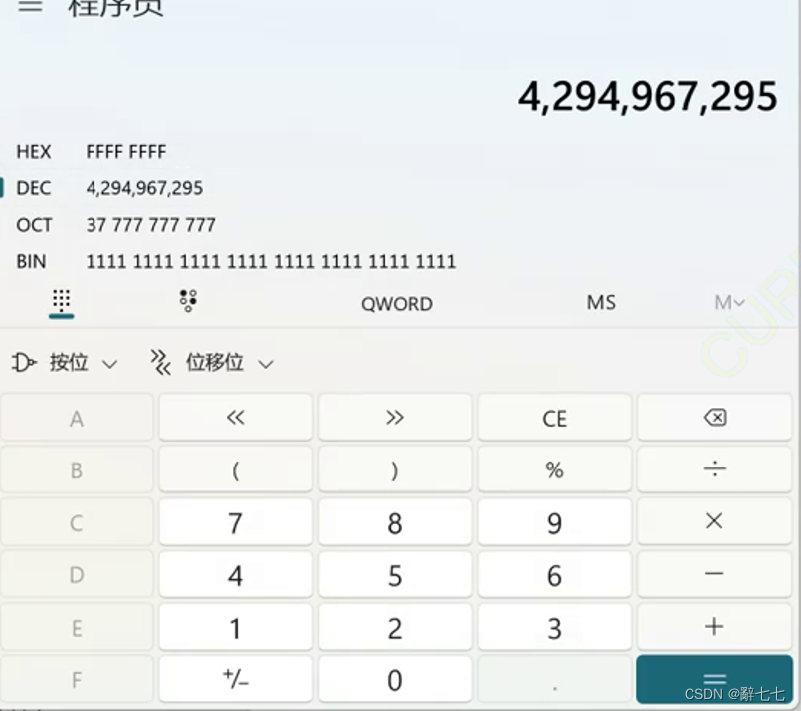
> unsigned 用来打印无符号数，所以当i=-1时，unsigned int i并不会认为i是一个负数，只会认为他是一个很大的正数，-1的补码为 **11111111111111111111111111111111**  
>  32个全一在计算机的值如下  
>  ![在这里插入图片描述](https://img-blog.csdnimg.cn/b34676cdd1f44561b05d9c782229f189.png)
> 
> 
> 


**练习6**

#include <stdio.h>
//char 类型的取值范围是 -128~127
int main()
{
char a[1000];
int i;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
}
//-1 -2 -3 -4 -5 -6 …-127 -128 -129 … -998 -999 -1000
//char -1 -2 -3 -128 127 126 … 3 2 1 0 -1 -2 -3 … -128 127 …
//1000个值
printf(“%d”, strlen(a));
//strlen 求字符串长度，找到是\0，\0的ASCII码值是0.
return 0;
}

运行结果;  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/9e018ad138bc4e0bbdc3993df317a1c2.png)  
 二进制加一减一的图解  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/ec0adce01e8642c886d77740211290d1.png)  
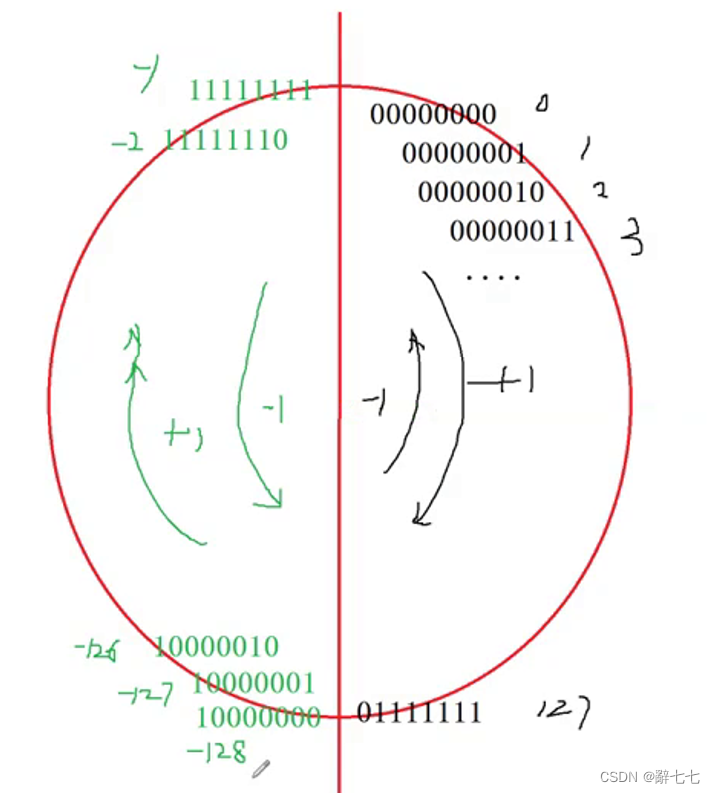
 **练习7**

#include <stdio.h>
unsigned char i = 0;
//0~255
int main()
{
for (i = 0; i <= 255; i++)
{
printf(“hello world\n”);
}
return 0;
}

> 
> i的范围是0~255，所以循环里的内容恒成立，所以结果为死循环。
> 
> 
> 


## 3. 浮点型在内存中的存储


常见的浮点数：



> 
> 3.14159  
>  1E10  
>  浮点数家族包括： float、double、long double 类型。  
>  浮点数表示的范围：float.h中定义
> 
> 
> 


![在这里插入图片描述](https://img-blog.csdnimg.cn/1ded224a031c4d91b2580666672fdf73.png)


### 3.1 一个例子


浮点数存储的例子：

#include <stdio.h>
int main()
{
int n = 9;
//00000000000000000000000000001001 - 9的补码
float* pFloat = (float*)&n;
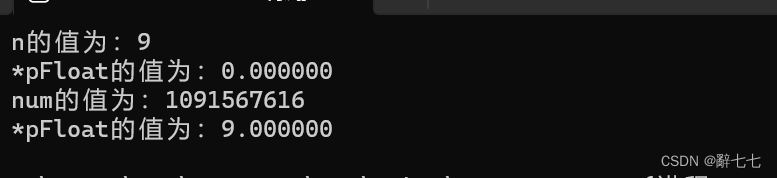
printf(“n的值为：%d\n”, n);
printf(“*pFloat的值为：%f\n”, *pFloat);
*pFloat = 9.0;
printf(“num的值为：%d\n”, n);
printf(“*pFloat的值为：%f\n”, *pFloat);
return 0;
}

输出结果：  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/d428c160987448e096040dcccb06a0a8.png)


### 3.2 浮点数存储的规则


num 和 \*pFloat 在内存中明明是同一个数，为什么浮点数和整数的解读结果会差别这么大？  
 要理解这个结果，一定要搞懂浮点数在计算机内部的表示方法。  
 详细解读：  
 根据国际标准IEEE（电气和电子工程协会） 754，任意一个二进制浮点数V可以表示成下面的形式：



> 
> * (-1)^S \* M \* 2^E
> * (-1)^S表示符号位，当S=0，V为正数；当S=1，V为负数。
> * M表示有效数字，大于等于1，小于2。
> * 2^E表示指数位。
> 
> 
> 


以5.5举例来说  
 十进制的5.5，写成二进制是 101.1  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/4c5a118e73804c3fb20d1d700f5dbda0.png)  
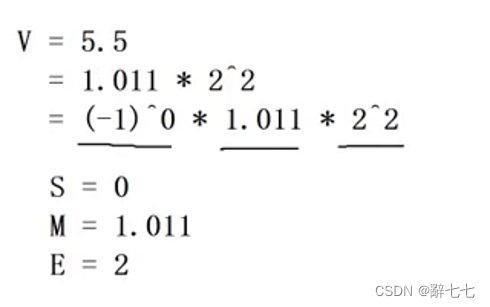
 **IEEE 754规定：**  
 对于32位的浮点数，最高的1位是符号位s，接着的8位是指数E，剩下的23位为有效数字M。  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/c8023cda094145fa92ae388deb617e03.png)  
 对于64位的浮点数，最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/1cbfd10b431148e087811e89d2a2c009.png)  
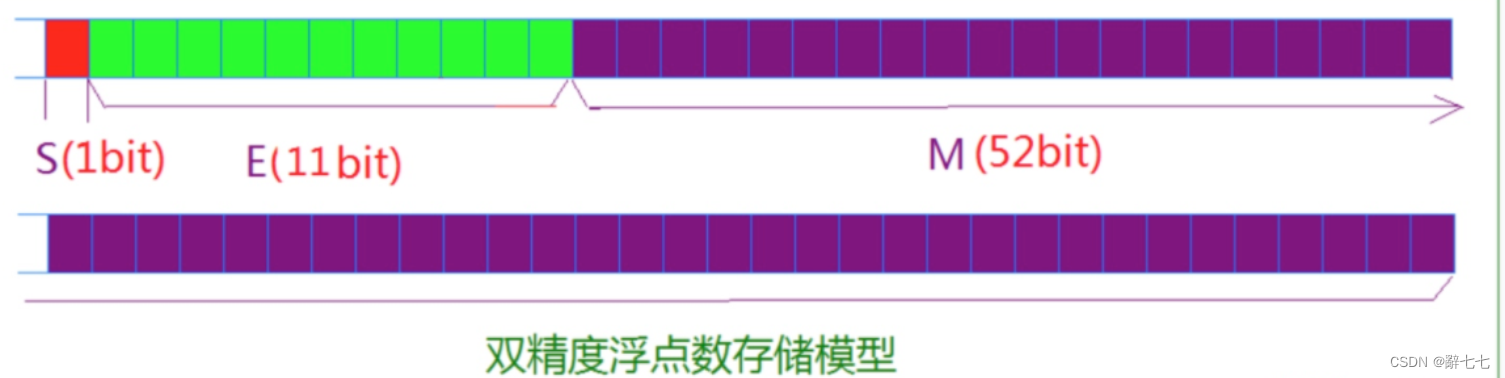
 **IEEE 754对有效数字M和指数E，还有一些特别规定。**  
 前面说过， 1≤M<2 ，也就是说，M可以写成 1.xxxxxx 的形式，其中xxxxxx表示小数部分。  
 IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。  
 以32位浮点数为例，留给M只有23位，将第一位的1舍去以后，等于可以保存24位有效数字。  
 **至于指数E，情况就比较复杂。  
 首先，E为一个无符号整数（unsigned int）**  
 这意味着，如果E为8位，它的取值范围为0255；如果E为11位，它的取值范围为02047。但是，我们知道，科学计数法中的E是可以出现负数的，所以IEEE 754规定，存入内存时E的真实值必须再加上一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。  
 比如，2^10的E是10，所以保存成32位浮点数时，必须保存10+127=137，即10001001.  
 例如：

#include <stdio.h>
int main()
{
float f = 5.5f;
//101.1
//(-1)^0 * 1.011 * 2^2 科学表现形式
//01000000101100000000000000000000 二进制表现形式
//40b00000 十六进制表现形式
//
return 0;
}

在内存中的存储为十六进制表现形式（由于大小端的原因，顺序有所不同）  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/e69aa586c2c1473a8729f979e1139562.png)


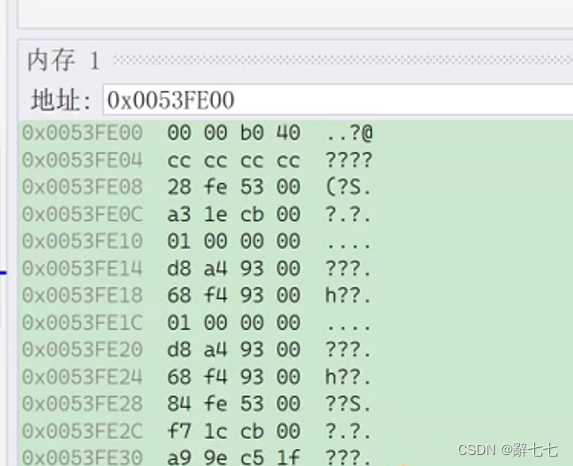
然后，指数E从内存中取出还可以再分成三种情况：  
 **E不全为0或不全为1**



> 
> 这时，浮点数就采用下面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将 有效数字M前加上第一位的1。 比如：  
>  0.5（1/2）的二进制形式为0.1，由于规定正数部分必须为1，即将小数点右移1位，则为  
>  1.0\*2^(-1)，其阶码为-1+127=126，表示为 01111110，而尾数1.0去掉整数部分为0，补齐0到23位00000000000000000000000，  
>  则其二进 制表示形式为:
> 
> 
> 

0 01111110 00000000000000000000000

**E全为0**



> 
> 这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，  
>  有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于 0的很小的数字。
> 
> 
> 


**E全为1**



> 
> 这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；
> 
> 
> 


好了，关于浮点数的表示规则，就说到这里。  
 **解释前面的题目：**  
 下面，让我们回到一开始的问题：为什么 0x00000009 还原成浮点数，就成了0.000000 ？  
 首先，将 0x00000009 拆分，得到第一位符号位s=0，后面8位的指数 E=00000000，最后23位的有效数字 M=000 0000 0000 0000 0000 1001。



> 
> 9 -> 0000 0000 0000 0000 0000 0000 0000 1001
> 
> 
> 


由于指数E全为0，所以符合上一节的第二种情况。因此，浮点数V就写成：


![img](https://img-blog.csdnimg.cn/img_convert/28bc2665518f52cec1ce9bdb5ff6c4ae.png)
![img](https://img-blog.csdnimg.cn/img_convert/74f5c43d21018df160b65d0b5dc33f81.png)

**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**[需要这份系统化资料的朋友，可以戳这里获取](https://bbs.csdn.net/topics/618545628)**


**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**

数 E=00000000，最后23位的有效数字 M=000 0000 0000 0000 0000 1001。



> 
> 9 -> 0000 0000 0000 0000 0000 0000 0000 1001
> 
> 
> 


由于指数E全为0，所以符合上一节的第二种情况。因此，浮点数V就写成：


[外链图片转存中...(img-70pkXwFS-1715808423188)]
[外链图片转存中...(img-fU6BSIzi-1715808423188)]

**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**[需要这份系统化资料的朋友，可以戳这里获取](https://bbs.csdn.net/topics/618545628)**


**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**