排序
“排序”顾名思义就是把乱序的变成有序的,就像我们玩斗地主这种牌类游戏时,我们拿到牌都会将牌给排序一下,更好的在对局中方便思考和观察,我们排序算法也亦是如此。
一、冒泡排序
冒泡排序的过程就像是我们在烧水时,气泡大的会向上冒,气泡小的则在下面,就是冒泡的一个过程,数字大的就是大气泡,数字小的就是小气泡,例如:

过程:从第一个数开始和后面一个数进行比较,大了便交换,否则便下一个次比较,如上图所示,用4与5进行比较,4 < 5,则用5与6比较,5 < 6, 则用6与3比较,6 > 3,则交换位置,以此类推6到了最后一个位置则这一个过程则称为第一次冒泡,每一次冒泡就是将未排序的数组中最大数向上推的过程。
代码实例:
public class BubbleSort {
/*
//将给定的数组排序
public static void sort(Comparable[] arr) {
//有几个数就需要比较几次,数比较大的就交换
for (int i = 1; i < arr.length; i++) {
//前一个数和后一个数比较
for (int j = 0; j < arr.length - 1; j++) {
if (compare(arr[j],arr[j + 1])) {
swap(arr,j,j + 1);
}
}
}
}
*/
//将上面的代码进行改进 => 每次比较后最大的数都将位于数组的最后一位,
// 所以每次排序都可以把原本最后一次比较省略掉
public static void sort(Comparable[] arr) {
for (int i = arr.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (compare(arr[j], arr[j + 1])) {
swap(arr, j, j + 1);
}
}
}
}
//比较元素大小
public static boolean compare(Comparable a, Comparable b) {
return a.compareTo(b) > 0;
}
//交换元素
public static void swap(Comparable[] arr, int i, int j) {
Comparable temp;
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
测试一下:

运行结果
冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
二、选择排序
选择排序的过程是:在待排序的数组中选择一个最小的元素放在起始位置,直到数组排序完,如下图所示:
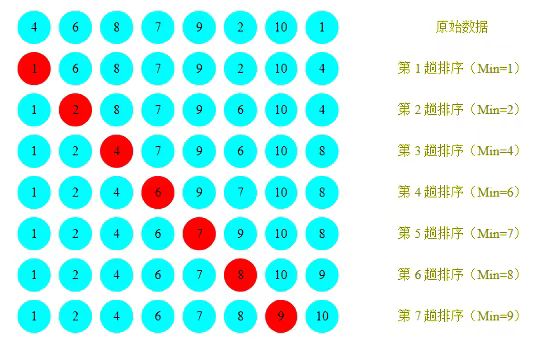
我们首先假定数组第一个数的下标是最小值的下标索引,然后一次向后比较,遇到较小的数便与其交换下标索引,每次比较完后最小值的下标索引便与待排数组的收尾进行交换,这样便会保证每次交换到的都是待排数组中最小的值,我们可以观察到我们需要进行n-1次排序。
代码实现:
public class SelectSort {
public static void sort(Comparable[] arr) {
//总共需要比较n - 1次
for (int i = 0; i < arr.length - 1; i++) {
//定义一个的下标索引,记录最小值的下标
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
if (compare(arr[minIndex], arr[j])) {
minIndex = j;
}
}
//每次比较完,都要交换i和minIndex下标的值
swap(arr, i, minIndex);
}
}
//比较元素大小
public static boolean compare(Comparable a, Comparable b) {
return a.compareTo(b) > 0;
}
//交换元素
public static void swap(Comparable[] arr, int i, int j) {
Comparable temp;
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
测试一下:

运行结果:

直接选择排序的特性总结:
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
三、插入排序
插入排序的过程就像是,我们在打扑克牌或麻将一样,我们要将没有排序的牌进行排序就需要拿起一张牌,然后将其想前比对,比前面的牌小则交换,反之则不变那便是这张牌所属的位置,例如:

我们将第一位数看做已排好序的,然后后面的剩余的为待排序的,我们进行比较,在合适的位置进行插入,依次类推便得到排好序的结果。
代码实现:
public class InsertSort {
public static void sort(Comparable[] arr) {
//将数组的首个数字表示为已排序的,后面的未排序的,然后遍历已排序的数组,进行插入
for (int i = 1; i < arr.length; i++) {
//将数组下标j 和下标j - 1的值进行比较,如果下标j - 1的值大于下标j的值则交换数据,反之则为找到合适的位置,退出循环
for (int j = i; j > 0; j--) {
if (compare(arr[j - 1], arr[j])) {
swap(arr, j -1, j);
} else {
break;
}
}
}
}
//比较元素大小
public static boolean compare(Comparable a, Comparable b) {
return a.compareTo(b) > 0;
}
//交换元素
public static void swap(Comparable[] arr, int i, int j) {
Comparable temp;
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
测试一下:

运行:

直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
四、希尔排序
希尔排序的过程与插入排序的过程大同小异,又称“缩小增量排序”,是插入排序的升级版,变得更高效一点。具体就是我们先定义一个增量h,然后利用这个增量对数组进行分组,分组完以后进行插入排序,得到的便是接近有序的数组:然后缩小其增量,然后执行上述操作,使增量h缩小至1时,排序后便是有序数组。相对于增量h也有其相关的定义规则和缩小规则:
//确定增长量h的最大值
int h=1;
while(h<N/2){
h=h*2+1;
}
h的减小规则为:
h=h/2
我们给出例图更直观的感受一下:

归纳一下排序原理:
1.选定一个增长量h,按照增长量h作为数据分组的依据,对数据进行分组;
2.对分好组的每一组数据完成插入排序;
3.减小增长量,最小减为1,重复第二步操作
代码实现:
public class ShellSort {
public static void sort(Comparable[] arr) {
//数组长度
int N = arr.length;
//确定增量h的值
int h = 1;
while (h < N) {
h = h * 2 + 1;
}
//当h<1时,排序结束
while (h >= 1){
//1.找到待插入的元素
for (int i = h; i < N; i++) {
//arr[i]就是待插入的元素
//然后将arr[i]插入到分好组的序列中arr[i - h],arr[i - 2h]...
for (int j = i; j >= h; j-=h) {
//将arr[j - h]与arr[j]进行比较,较大则交换,
//反之则退出此次循环
if (compare(arr[j - h], arr[j])) {
swap(arr,j-h, j);
} else {
break;
}
}
}
//2.缩小增量h
h /= 2;
}
}
//比较元素大小
public static boolean compare(Comparable a, Comparable b) {
return a.compareTo(b) > 0;
}
//交换元素
public static void swap(Comparable[] arr, int i, int j) {
Comparable temp;
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
测试一下:

运行:

希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定:


五、归并排序
归并排序的过程,是分治法的应用过程,将一组数据尽可能的拆分成两组相同的数据,并对每一组数据在拆分,直到数据的大小为1不可再拆时,我们就向上返回,进行排序,实际也是一种递归的过程,分治法顾名思义就是“分”=>分组,“治”=>共治,两个步骤组成,光光有文字叙述,我觉得会有点难以理解,我们上图看一下,体会这个过程:

简单概述一下就是:
1.我们对数据进行分组
2.相邻的两组进行合并
在上图我们发现了,其每组的过程都是一样的,只是数据不同,那我们肯定要运用到递归来实现,我们接下来用代码实现在分析:
public class MergeSort {
//定义一个辅助数组assist
private static Comparable[] assist;
//将数据进行分组排序
public static void sort(Comparable[] arr) {
assist = new Comparable[arr.length];
//定义左右指针,表示需要进行分组的范围
int left = 0;
int right = arr.length - 1;
//利用sort的重构方法进行分组排序
sort(arr, left, right);
}
public static void sort(Comparable[] arr, int left, int right) {
//安全性校验
if (right <= left) return;
//定义中间指针,进行拆分
int mid = left + (right - left) / 2;
//递归不断拆分
sort(arr, left, mid);
sort(arr, mid + 1, right);
//进行合并
merge(arr,left,mid,right);
}
//归并
public static void merge(Comparable[] arr, int left, int mid, int right) {
int index = left;//这个是指向assist数组开始填充的指针
int p1 = left;//这个是指向第一组数据的第一个数
int p2 = mid + 1;//指向第二组数据的第一个数
//两组数据依次进行比较,较小的数填充到assist数组中,指针向后移,
//循环结束条件就是有一组数据已经遍历完了,退出
while (p1 <= mid && p2 <= right) {
if (compare(arr[p1], arr[p2])) {
//如果arr[p1] 大于 arr[p2],则填充arr[p2]
assist[index++] = arr[p2++];
}else {
//反之则填充arr[p1]
assist[index++] = arr[p1++];
}
}
//跳出循环后,表示有一组数据已经遍历完了,那我们需要将剩下一组没有遍历完的数据直接顺序填充即可,因为同一组数据本身就是一排好序的
//但是我们并不知道的是那组数据先结束,所以都需要进行判断
while (p1 <= mid) {
assist[index++] = arr[p1++];
}
while (p2 <= right) {
assist[index++] = arr[p2++];
}
//我们只需将我们排好序的辅助数组assist复制到原数组即可
for (int i = 0; i <= right; i++) {
arr[i] = assist[i];
}
}
//比较元素大小
public static boolean compare(Comparable a, Comparable b) {
return a.compareTo(b) > 0;
}
//交换元素
public static void swap(Comparable[] arr, int i, int j) {
Comparable temp;
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
整个的代码量还是相对较多的,但具体都挺好理解的,我们自己画一画整个过程,明白了其具体流程,我们在敲代码的时候也是手到擒来哈哈哈,其中我们要注意的是一些边界条件,如果边界条件没有弄清楚,很容易就迷了,多多练习,理解每一次都会有不同的收获.
其中我们利用辅助数组对其填充,就是比较两组数据大小,然后填到一个空数组中的一个过程,如图:

我们进行测试一下:


归并排序总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
六、快速排序
快速排序是对冒泡排序的一种改进。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
排序原理:
1.首先设定一个分界值,通过该分界值将数组分成左右两部分;
2.将大于或等于分界值的数据放到到数组右边,小于分界值的数据放到数组的左边.此时左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值;
3.然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
4.重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左侧和右侧两个部分的数据排完序后,整个数组的排序也就完成了。
具体的我们还是得通过图例才能更好的表现出来:


代码实现:
public class QuickSort {
public static void sort(Comparable[] arr) {
int p1 = 0;//首个元素的下标
int p2 = arr.length - 1;//最后一个元素的下标
//将数据的p1~p2元素进行排序
sort(arr, p1, p2);
}
public static void sort(Comparable[] arr, int p1, int p2) {
//安全性检查
if (p2 <= p1) return;
//对数据进行切分
int partition = partition(arr, p1, p2);
//partition的下标的值是基准值,我们将其左右两部分分开排序
//将p1~partition - 1的元素进行排序
sort(arr,p1,partition - 1);
//将partition + 1~p2之间的元素进行排序
sort(arr,partition + 1, p2);
}
public static int partition(Comparable[] arr, int p1, int p2) {
//我们通常定义首个元素为基准值
Comparable key = arr[p1];
//定义左右指针,分别指向首元素和尾元素
int left = p1;
int right = p2 + 1;
//进行切分
//从右往左找比基准值小的数
//从左往右找比基准值大的数
while (true) {
// 1.首先从右往左扫描
while (compare(arr[--right], key)) {
//如果扫描完发现都没有比基准值小的数,则退出循环
if (right == p1) break;
}
// 2.从左往右扫描
while (compare(key, arr[++left])) {
//如果扫描完发现都没有比基准值大的数,则退出循环
if (left == p2) break;
}
//当左指针和右指针相遇时,则表示扫描完毕,即可退出循环
if (left >= right) {
break;
} else {
//当左右指针还没有相遇时,找到相应的数了,交换位置
swap(arr, left, right);
}
}
//每趟循环完成,交换基准值和左右指针相遇位置的值即可
swap(arr, p1, right);
//左右指针相遇的地方就是切分的位置,所以这里返回left或者right都可以
return right;
}
//比较元素大小
public static boolean compare(Comparable a, Comparable b) {
return a.compareTo(b) > 0;
}
//交换元素
public static void swap(Comparable[] arr, int i, int j) {
Comparable temp;
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
测试一下:


快速排序总结:
-
快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
-
时间复杂度:O(N*logN)

-
空间复杂度:O(logN)
-
稳定性:不稳定
总结
这里总结了我们常见算法的一些原理,是自己学习过程中的一些总结,希望对大家也有所帮助.
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








