lasso回归和岭回归

岭回归和lasso回归

事实上回归中关于自变量的选择大有门道，变量过多时可能会导致多重共线性问题造成回归系数的不显著，甚至造成OLS估计的失效。

本节介绍到的岭回归和lasso回归在OLS回归模型的损失函数上加上了不同的惩罚项，该惩罚项由回归系数的函数构成，一方面，加入的惩罚项能够识别出模型中不重要的变量，对模型起到简化作用，可以看作逐步回归法的升级版;另一方面，加入的惩罚项能够让模型变得可估计即使之前的数据不满足列满秩

古典回归模型的4个假定

一:线性假定

这里的线性假定是值可以替换后成为线性的函数

二:严格外生性

E(ui|x)=0

从实际意义来看就是扰动项和任意一个自变量都不相关

保证估计出来的回归系数无偏且一致

三:无多重共线性

任意一个解释变量都不能是其他解释变量的线性组合。

保证可以估计出来正确的值

四:球型扰动项:

相同方差,无自相关

扰动项可以表示为一个n阶的实矩阵

岭回归

损失函数:

对损失函数求导,并使其等于0:

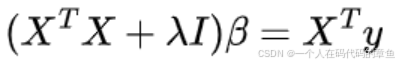
这样可以解出岭回归系数

接下来就是选择lambda

岭迹分析:观察岭迹图，选择系数趋于稳定且整体模型表现较好时对应的lambda值。

这里的岭迹图是β随着lambda变化的图

岭迹法选择入值的一般原则是:

(1)各回归系数的岭估计基本稳定

(2)用最小二乘估计时符号不合理的回归系数，其岭估计的符号变得合理

(3)回归系数没有不合乎经济意义的绝对值

(4)残差平方和增大不太多。

计算岭回归系数

在确定了lambda值之后，根据岭回归的公式计算岭回归系数。岭回归的估计公式为：

 模型评估和预测

模型评估：

可以使用均方误差（MSE）、平均绝对误差（MAE）等指标评估模型在训练集或测试集上的性能。

 结果分析

系数解释：分析岭回归系数，了解每个自变量对因变量的影响。由于岭回归对系数进行了收缩，系数的大小和正负反映了自变量对因变量的相对重要性和影响方向。

模型稳定性：比较不同  值下的系数和预测结果，观察模型的稳定性。较大的  会使系数收缩更严重，但可能会提高模型在不同数据集上的稳定性。

 优缺点

优点：

提高稳定性：通过对系数进行约束，岭回归能够有效降低系数的方差，提高模型在不同数据集上的稳定性，减少过拟合的风险。

处理多重共线性：对于存在多重共线性的自变量，岭回归能够给出相对合理且稳定的系数估计，使模型具有更好的解释性和预测能力。

缺点：

参数选择依赖经验：正则化参数  的选择对模型性能影响较大，虽然有交叉验证等方法辅助选择，但在实际应用中仍需要一定的经验和多次试验。

所有特征都保留：岭回归不会使系数精确为零，即所有特征都会保留在模型中，这可能导致模型相对复杂，解释性不如一些能够进行特征选择的方法（如 Lasso 回归）。

lasso回归

最小绝对收缩和选择算子回归）由斯坦福大学的罗伯特・泰比希拉尼（Robert Tibshirani）于 1996 年提出 ，是一种用于线性回归模型的正则化方法。它在解决多重共线性问题和进行特征选择方面具有显著优势，

损失函数

正则化参数入

求解回归系数

模型评估

模型应用和解释

优缺点

优点：

特征选择：能够自动识别并剔除对目标变量影响较小的特征，实现数据降维，使模型更加简洁，易于解释。

处理共线性：对存在多重共线性的数据具有较好的处理能力，通过特征选择，避免了因共线性导致的系数估计不稳定问题。

预测性能：在某些情况下，经过特征选择后的 Lasso 回归模型能够在预测准确性上优于普通线性回归模型，特别是在高维数据和存在噪声数据的场景中。

缺点：

参数选择敏感：正则化参数入的选择对模型性能影响较大，不同的 入值可能导致模型选择不同的特征子集，进而影响模型的预测能力和可解释性。虽然有多种选择入 的方法，但在实际应用中仍需要仔细调整。

计算复杂度：相比于普通线性回归，Lasso 回归的求解方法（如坐标下降法、近端梯度下降法）通常具有更高的计算复杂度，尤其是在处理大规模数据时，计算时间可能较长。

下面直接展示lasso回归的应用

例题：

年份	单产	种子费	化肥费	农药费	机械费	灌溉费
1990	1017	106.05	495.15	305.1	45.9	56.1
1991	1036.5	113.55	561.45	343.8	68.55	93.3
1992	792	104.55	584.85	414	73.2	104.55
1993	861	132.75	658.35	453.75	82.95	107.55
1994	901.5	174.3	904.05	625.05	114	152.1
1995	922.5	230.4	1248.75	834.45	143.85	176.4
1996	916.5	238.2	1361.55	720.75	165.15	194.25
1997	976.5	260.1	1337.4	727.65	201.9	291.75
1998	1024.5	270.6	1195.8	775.5	220.5	271.35
1999	1003.5	286.2	1171.8	610.95	195	284.55
2000	1069.5	282.9	1151.55	599.85	190.65	277.35
2001	1168.5	317.85	1105.8	553.8	211.05	290.1
2002	1228.5	319.65	1213.05	513.75	231.6	324.15
2003	1023	368.4	1274.1	567.45	239.85	331.8
2004	1144.5	466.2	1527.9	487.35	408	336.15
2005	1122	449.85	1703.25	555.15	402.3	358.8
2006	1276.5	537	1888.5	637.2	480.75	428.4
2007	1233	565.5	2009.85	715.65	562.05	456.9

1，数据的预处理（标准化，统一量纲）

这里的量纲是一样的

Matlab可以使用zscore来进行标准化，SPSS可以使用分析->描述统计->描述获取标准化数据

如果是不一样的量纲就需要在state中使用  egen name = std(标签)一个一个的进行标准化

2，K折交叉验证调整参数法

cvlasso y x1 x2 x3..... ,lopt seed(777)

3，得出结果

得到的图表第一列是lambda，第二列是均分预测误差，第3列是标准差

得到的结果会有个*标记的

这里表示最小的预测误差是6464.7286，对应的lambda就是69.020233

下面是回归系数

第一列是lasso回归的结果，第二列是只使用lasso回归筛选出来的3个变量进行回归得到的结果

所以lasso回归的重要用处就是筛选重要变量

什么时候用？

特征选择

自动筛选关键特征：Lasso 回归通过在损失函数中添加 L1 范数正则化项，能使部分特征的系数变为 0，从而自动识别并剔除对目标变量影响较小的特征。在高维数据场景，如基因表达数据分析，基因数量众多，Lasso 回归可找出与疾病相关的关键基因，简化模型结构，提升可解释性。

避免维度灾难：当数据维度极高时，计算量会急剧增加，且容易出现过拟合。Lasso 回归的特征选择功能能降低数据维度，减少计算负担，有效避免维度灾难问题，提升模型在高维数据上的表现。

处理多重共线性

稳定系数估计：在自变量存在多重共线性时，普通线性回归系数估计不稳定，方差大。Lasso 回归通过正则化，收缩系数，使估计更稳定，给出更可靠的系数估计值。例如在经济数据建模中，多个经济指标间常存在相关性，Lasso 回归可应对这种情况。

增强模型稳健性：处理多重共线性后，模型对数据波动更具抵抗力，在不同数据集上表现更稳定，提高模型的泛化能力，降低过拟合风险。

提升预测性能

优化模型复杂度：Lasso 回归在特征选择过程中，去除冗余和无关特征，保留关键特征，使模型复杂度与数据复杂度相匹配，避免过拟合，提高预测准确性。

提高泛化能力：通过合理选择特征和控制模型复杂度，Lasso 回归模型在未知数据上的预测表现更好，能更准确地对新样本进行预测，广泛应用于预测房价、销量等实际问题。

数据降维

减少数据维度：Lasso 回归将众多特征中不重要的特征系数置零，相当于从原始高维数据中挑选出关键特征组成低维数据集，实现数据降维，且降维过程基于特征对目标变量的贡献，保留重要信息。

便于数据处理和存储：降维后的数据量减少，降低数据处理和存储成本，在数据存储和传输受限的场景中优势明显。