最全快速傅里叶变换学习及C语言实现_快速傅里叶变换c语言实现(1)，2024年最新C C++基础语言教程

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化的资料的朋友，可以添加戳这里获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

#define M_PI 3.14159265358979323846 //PI 双精度

//由于蝶形运算的需要，根据奇偶坐标将元素分到数组的前后各半部分
void separate(complex* a,int n) {
complex* b = new complex[n/2]; // get temp heap
for(int i=0; i<n/2; ++i) //copy所有奇下标元素
b[i] = a[i*2+1];
for(int i=0; i<n/2; ++i) //copy所有偶下标元素到数组lower-half
a[i] = a[i*2];
for(int i=0; i<n/2; ++i) //copy所有偶下标元素(form heap)到数组upper-half
a[i+n/2] = b[i];
delete[] b; //delete heap
}

//N必须是2的整数次幂
//X[]存储N个输入，FFT后依旧存储在X中
//由于Nyquit定理，仅仅前N/2 FFT结果有效(后N/2是镜射)
void fft2(complex* X,int N) {
if(N < 2) {
//递归终止
//do nothing,因为X[0] = x[0]
} else {
separate(X,N); //将偶坐标元素移至lower half,奇坐标元素移至upper half
fft2(X, N/2); //递归偶坐标元素
fft2(X+N/2, N/2); //递归奇坐标元素

	//合并两个递归结果
	for(int k=0; k<N/2; ++k) {
		complex<double> e = X[k];     //偶
		complex<double> o = X[k+N/2]; //奇
		//w是蝶形系数
		complex<double> w = exp( complex<double>(0,-2.0\*M_PI\*k/N) );
		X[k    ]   = e + w \* o;
		X[k+N/2]   = e - w \* o;
	}
}

}
//测试
int main() {
const int nSamples = 8;
complex x[nSamples]; // 存储采样数据
complex X[nSamples]; // 存储FFT结果

//生成测试样本
for(int i=0; i<nSamples; ++i) {
	x[i] = complex<double> (0.0,0.0);
	x[i].real() = (double)i;
	x[i].imag() = 0.0;

	X[i] = x[i];		//拷贝至X，为FFT做准备
}

//计算fft
fft2(X,nSamples);
for(int i=0; i<nSamples; ++i ) 
	printf("%0.3f \t %0.3f\n",X[i].real(),X[i].imag());

}

##### 四、快速傅里叶变换迭代实现


FFT 的实现可以自顶而下，采用递归，但是对于硬件实现成本高，对于软件实现都不够高效，改用迭代较好，自底而上地解决问题。感觉和归并排序的迭代版很类似，不过先要采用“位反转置换”的方法把 Xi 放到合适的位置。


###### 位反转算法- 雷德算法


一个小算法的感觉。  
 拿一个0到2^n-1的自然数序列。  
 比方说  
 0 1 2 3 4 5 6 7  
 我们转换为二进制状态，那么这个序列就是



> 
> 000 001 010 011 100 101 110 111
> 
> 
> 


接下来我们模拟FFT的位置交换，即：



> 
> 0 1 2 3 4 5 6 7  
>  0 2 4 6 1 3 5 7  
>  0 4 2 6 1 5 3 7
> 
> 
> 


发现最终的序列变为了



> 
> 000 100 010 110 001 101 011 111  
>  雷德算法就是用于求出这个倒序的数列。
> 
> 
> 



> 
> 由上面的表可以看出，按自然顺序排列的二进制数，其后面一个数总是比其前面一个数大1，即后面一个数是前面一个数在最低位加1并向高位进位而得到的。  
>  而倒位序二进制数的后面一个数是前面一个数在最高位加1并由高位向低位进位而得到。  
>  I、J都是从0开始，若已知某个倒位序J，要求下一个倒位序数：  
>  应先判断J的最高位是否为0。  
>  这可与k=N/2相比较，因为N/2总是等于100的。  
>  如果k>J，则J的最高位为0，只要把该位变为1（J与k=N/2相加即可），就得到下一个倒位序数；  
>  如果K<=J，则J的最高位为1，可将最高位变为0（J与k=N/2相减即可）。然后还需判断次高位，这可与k=N\4相比较，若次高位为0，  
>  则需将它变为1（加N\4即可）其他位不变，既得到下一个倒位序数；若次高位是1，则需将它也变为0。然后再判断下一位……
> 
> 
> 


代码实现：

//假设N为2的整数次幂
void RaderReverse(int *arr, int N) {
int j,k;
//第一个和最后一个数位置不变，故不处理
for(int i=1,j=N/2; i<N-1; ++i) {
//原始坐标小于变换坐标才交换，防止重复
if(i<j) {
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
}
k = N/2; // 用于比较最高位
while(k <= j) { // 位判断为1
j = j-k;// 该位变为0
k = k/2;// 用于比较下一高位
}
j = j+k;// 判断为0的位变为1
}
}

###### 时间抽取 DIT Radix－2算法


![在这里插入图片描述](https://img-blog.csdnimg.cn/20181129224925408.png)  
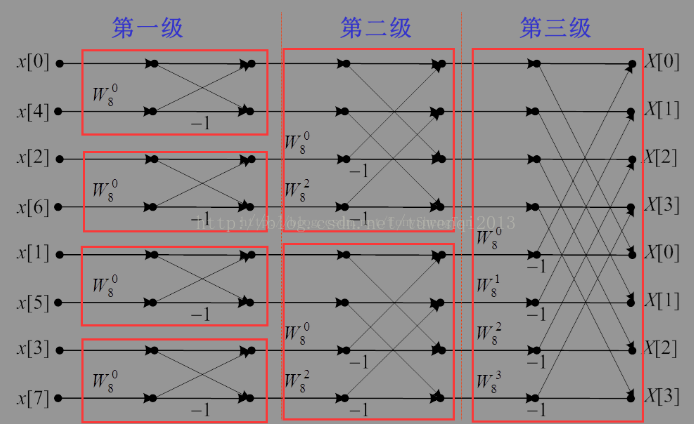
 该算法的特征是：  
 1）输入序列顺序位反转，输出所有频率值都是按顺序出现的。  
 2）计算可以“就地”完成，也就是蝶形所使用的存储位置可以被重写。  
 3）从图中我们可以看到对于点数为N = 2^L的FFT运算，可以分解为L阶蝶形图级联，每一阶蝶形图内又分为M个蝶形组，每个蝶形组内包含K个蝶形。（迭代算法实现：根据这一点我们就可以构造三阶循环来实现蝶形运算。编程过程需要注意旋转因子与蝶形阶数和蝶形分组内的蝶形个数存在关联。）  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/2018113015161631.gif)


###### 快速傅里叶变换迭代算法实现


该代码在上文的基础上，参考了[FFT(快速傅里叶) c语言版](https://bbs.csdn.net/topics/618668825)的思想。


代码实现：

//g++ fft2.cpp -o fft2 -lm
#include
#include
using namespace std;

#define M_PI 3.14159265358979323846 //PI 双精度
//假设N为2的整数次幂
void RaderReverse(complex *arr, int N) {
int j,k;
//第一个和最后一个数位置不变，故不处理
for(int i=1,j=N/2; i<N-1; ++i) {
//原始坐标小于变换坐标才交换，防止重复
if(i<j) {
complex temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
}
k = N/2; // 用于比较最高位
while(k <= j) { // 位判断为1
j = j-k;// 该位变为0
k = k/2;// 用于比较下一高位
}
j = j+k;// 判断为0的位变为1
}
}
void fft(complex *x,int n) {
int i=0,j=0,k=0,l=0;
complex up,down,product;
RaderReverse(x,n);

//w是蝶形系数
complex<double>\* W = new complex<double>[n]; 
for(int i=0;i<n;++i) {
	W[i] = exp( complex<double>(0,-2.0\*M_PI\*i/n) );
	//printf("%0.3f \t %0.3f\n",W[i].real(),W[i].imag());
}

for(i=0; i<log(n)/log(2); ++i)  /\*log(n)/log(2) 级蝶形运算 stage \*/  
{
	l = 1<<i;
	for(j=0;j<n;j+= 2\*l) /\*一组蝶形运算 group,每组group的蝶形因子乘数不同\*/ 
	{
		for(k=0;k<l;++k) /\*一个蝶形运算 每个group内的蝶形运算的蝶形因子乘数成规律变化\*/  
		{
			product = x[j+k+l]\*W[n\*k/2/l];
			up   = x[j+k] + product;
			down = x[j+k] - product;
			x[j+k]   = up;
			x[j+k+l] = down;
		}
	}
}
delete[] W;				 //delete W 

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上C C++开发知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

如果你需要这些资料，可以戳这里获取

转存中…(img-DNtVCtxX-1715827320399)]

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上C C++开发知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

如果你需要这些资料，可以戳这里获取