C C++最全最小二乘法，2024年最新吃一堑长一智

本文链接：https://blog.csdn.net/2401_84978565/article/details/138878394

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差（真实目标对象与拟合目标对象的差）的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

最小二乘法还可用于曲线拟合。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。
选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小
最小二乘法也是一种优化方法，求得目标函数的最优值。并且也可以用于曲线拟合，来解决回归问题。回归学习最常用的损失函数是平方损失函数，在此情况下，回归问题可以著名的最小二乘法来解决。

简而言之，最小二乘法同梯度下降类似，都是一种求解无约束最优化问题的常用方法，并且也可以用于曲线拟合，来解决回归问题。

监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。

最小二乘法处理的一般模型表达式如下：
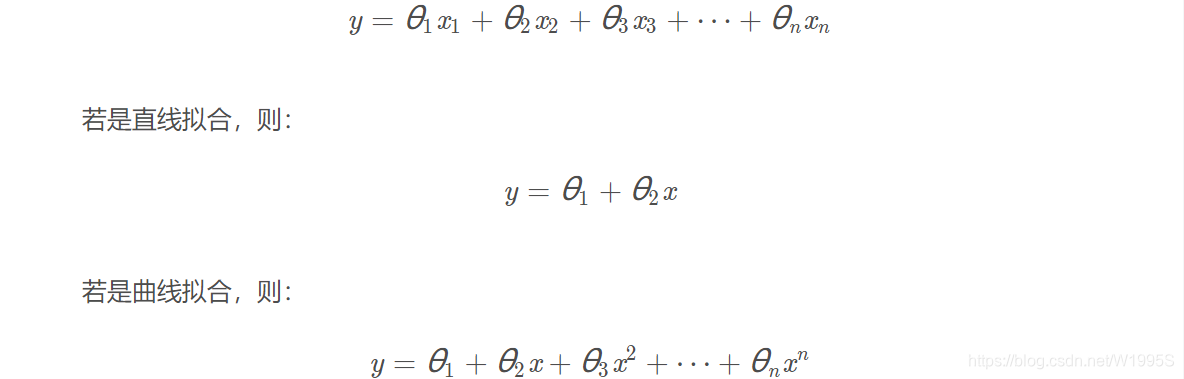
在这里插入图片描述
视问题复杂度而定x取几次方。这里可能有人有疑问，最小二乘不是处理线性问题吗？怎么 x^n都出来了？

注意，我们的目的是求取一个非线性方程，但当我们用最小二乘求解时，我们针对的是θ变量，而不是x ，也就是说，机器学习中，这里的x 是输入，是已知量，y 是输出，是预测量， θ 才是我们要学习的变量，所以这还是一个线性问题。

当然是真实值与拟合值的差
在这里插入图片描述
但为啥要平方（2范数）呢？绝对值（1范数）不可以吗？

因为误差是长度，还要取绝对值，计算起来麻烦，就干脆用平方来代表误差。而且平方要比绝对值更能得到最短距离，即使得误差最小化，也就是更能使得拟合函数逼近真实函数。

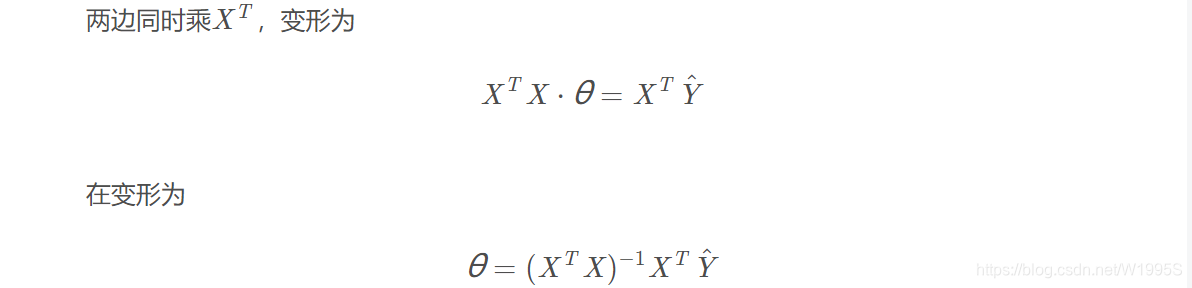
在这里插入图片描述

从上面的最后一个式子可以看出，只有当矩阵

X^T X

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**