聚类分析概述

前言

在数据科学和机器学习的广袤天地里，聚类分析如同一束穿透迷雾的光芒，指引着我们探索数据的深层秘密。作为数据挖掘和机器学习的重要分支，聚类分析不仅能够揭示数据集中的内在结构和模式，还能够为决策制定提供有力的支持。今天，就让我们一同走进聚类分析的奇妙世界，探索它如何成为解锁数据内在结构的钥匙。

想象一下，你手中握有一大堆看似杂乱无章的数据点，它们或高或低，或远或近，仿佛没有任何规律可循。然而，当你运用聚类分析的方法时，这些看似随机的数据点却开始呈现出某种神秘的规律。它们似乎被某种无形的力量牵引着，逐渐聚集成若干个紧密相连的群体。每一个群体都代表着一类相似的数据点，它们在某些特征上具有共同的属性或趋势。

聚类分析正是这样一种强大的工具，它能够帮助我们从海量数据中挖掘出潜在的群体结构和模式。无论是市场分析、客户细分，还是图像分割、文本聚类，聚类分析都发挥着举足轻重的作用。它不仅能够提高数据处理的效率，还能够为决策制定提供科学依据和数据支持。

在本文中，我们将全面剖析聚类分析的基本原理、方法和应用场景。我们将从数学的角度解读聚类算法的工作原理，从实践的角度展示聚类分析在各个领域中的广泛应用。我们还将深入探讨不同类型的聚类算法（如K-means、层次聚类、DBSCAN等）的优缺点和适用场景，以及如何处理高维数据和大规模数据集等挑战。

无论你是数据科学的新手，还是有一定经验的从业者，相信本文都能为你提供有益的参考和启示。让我们一起踏上这段聚类分析的探索之旅，共同揭开数据内在结构的神秘面纱吧！

一、定义

“聚类”作为数据分析中的一个核心概念，其定义确实具有一定的模糊性，这也是众多聚类算法并存的原因之一。尽管这些算法都旨在将数据集划分为若干组数据对象（即集群），但不同的研究者会根据实际需求和数据特性采用不同的聚类模型和算法。

这些聚类模型的核心共同点在于它们都是对数据集的一种划分方式，但划分依据和结果却各不相同。例如，有些模型基于数据对象之间的距离或相似性来构建集群，如K-means算法；而有些则基于数据点的密度或连通性，如DBSCAN算法。此外，还有基于图结构、神经网络等复杂模型的聚类方法。

不同的聚类模型在属性上差异显著。例如，基于距离的模型通常关注数据点之间的空间关系，而基于密度的模型则更注重数据点的局部密集程度。这些差异导致了不同算法在处理不同类型数据集时的优势和局限性。

因此，理解这些聚类模型是理解不同聚类算法之间差异的关键。在实际应用中，我们需要根据数据集的特性、分析目标和算法性能等因素来选择最合适的聚类模型和算法。只有这样，我们才能从海量数据中挖掘出有价值的信息，为决策提供科学依据和数据支持。

虽然“聚类”的概念难以精确定义，但正是这种模糊性为聚类分析提供了广阔的发展空间和应用前景。随着数据科学和机器学习技术的不断发展，相信未来会有更多创新的聚类算法和模型涌现出来，为数据分析领域注入新的活力。

• 连通性模型 ：例如，分层聚类基于距离连通性来构建模型。
• 质心模型 ：例如，k-means算法用单个均值向量表示每个聚类。
• 分布模型 ：聚类是使用统计分布建模的，例如由期望最大化算法使用的多元正态分布。
• 密度模型 ：例如，DBSCAN和OPTICS将集群定义为数据空间中连接的密集区域。
• 子空间模型 ：在双聚类(也称为共聚类或双模聚类)中，聚类由聚类成员和相关属性建模。
• 组模型 ：有些算法不提供精确的结果模型，只提供分组信息。
• 图模型 ：一个集团，即图中节点的子集，令该子集中的每两个节点通过一条边连接，可以认为这是聚类的原型。完全连通性要求的松弛(一部分边缘可能丢失)被称为准派系，如HCS聚类算法。
• 神经网络模型 ：最著名的无监督神经网络是自组织映射，这些模型通常可以被描述为类似于上述模型当中的一个或多个，并且当神经网络实现一种形式的主成分分析或独立成分分析的形式时，子空间模型也会被包括在内。

“聚类”本质上是一组这样的聚类，它通常包含数据集中的所有对象。此外，它可以指定集群彼此之间的关系，例如，彼此嵌入的集群的层次结构。聚类可以大致区分为:

• 硬聚类 ：每个对象是否属于一个集群
• 软聚类 (同时: 模糊聚类 ):每个对象在一定程度上属于每个集群(例如，属于集群的可能性)

还有更细微的区别，例如:

• 严格分区聚类 ：每个对象恰好属于一个集群
• 带有野值的严格分区聚类 ：对象也可以不属于任何集群，并且被视为野值
• 交叠聚类 (同时: 替代聚类, 多视图聚类 ) ：对象可能属于多个集群；通常涉及硬聚类
• 分级聚类 ：属于子聚类的对象也属于父聚类
• 子空间聚类 ：虽然交叠聚类在唯一定义的子空间内，但聚类不应该重叠

二、算法

如上所列，聚类算法可以根据它们的聚类模型进行分类。以下概述将仅列出聚类算法的最突出的例子，因为可能有超过100种已发布的聚类算法。不是所有的聚类算法都会为它们的集群提供模型，因此不容易分类。维基百科解释的算法概述可以在统计算法列表中找到。

现在这里没有客观“正确”聚类算法，但是正如所指出的，“聚类是旁观者的眼睛。”[5] 对于一个特定的问题，最合适的聚类算法通常需要通过实验来选择，除非有数学上的原因使一个聚类模型优于另一个。应该注意的是，为一种模型设计的算法通常会在包含完全不同类型模型的数据集上失败。[5] 例如，k-means算法找不到非凸集群。[5]

2.1 基于连通性的聚类(分层聚类)

基于连通性的集群，也称为 分层聚类，是基于一个核心概念，即物体与附近物体的关系比与远处物体的关系更密切。这些算法根据“对象”的距离将它们连接起来形成“集群”。集群很大程度上可以用连接集群的各个部分所需的最大距离来描述。在不同的距离，将形成不同的聚类，这可以用树图来表示，树图解释了通用名称“分层聚类”的来源:这些算法不提供数据集的单一划分，而提供了在特定距离彼此融合的广泛的聚类层次。在树形图中，y轴表示集群融合的距离，而对象沿着x轴放置，这样集群就不会混淆。

基于连通性的聚类是一整套以距离计算方式为区别的方法。除了通常选择的距离函数，用户还需要决定要使用的链接标准(因为一个集群由多个对象组成，所以有多个候选对象来计算距离)。一般通用的选择被称为单链聚类(最小物距)、完全连锁聚类(最大物距)和UPGMA或WPGMA(“具有算术平均的未加权或加权对组方法”，也称为平均链聚类)。此外，层次聚类可以是聚集(从单个元素开始，然后将它们聚集成集群)或分裂的(从完整的数据集开始，然后将其划分成分区)。

这些方法不会产生数据集的唯一分区，但是用户仍然需要从中选择适当集群的层次结构。它们对于野值的表现不是很稳定，野值要么会显示为额外的集群，要么甚至会导致其他集群合并(称为“链式现象”，特别是单链聚类)。在一般情况下，对于聚集聚类，复杂性是    ，且对于分裂聚类，复杂性是  ，[5] 这使得它们的处理速度对于大型数据集来说太慢。对于某些特殊情况，我们有已知的最佳有效方法(复杂性   ):用于单链聚类的SLINK[6] 和用于完全连锁聚类的CLINK[7] 。在数据挖掘社区，这些方法被认为是聚类分析的理论基础，但通常被认为是过时的。然而，它们确实为许多后来的方法提供了灵感，例如基于密度的聚类。

• 链接聚类的例子
• 

高斯数据上的单链接。在35个聚类中，最大的聚类开始分裂成更小的部分，而在此之前，由于单链效应，它仍然连接到第二大聚类。

基于密度的聚类上的单链接。提取了20个聚类，其中大部分只包含单个元素，因为链接聚类没有“噪声”的概念。

2.2 基于质心的聚类

在基于质心的聚类中，聚类由中心向量表示，该向量不一定是数据集的成员。当集群数量固定为 k, k-均值聚类给出了优化问题的正式定义:找到 k 聚类中心，并将对象分配到最近的聚类中心，使得离聚类的平方距离最小化。

优化问题本身被称为NP难题，因此常用的方法是只搜索近似解。一种特别著名的近似方法是劳埃德算法，[8] 通常简称为"k均值算法"(尽管另一种算法也采用了这个名称)。然而，它只会找到一个局部最优值，并且通常会以不同的随机初始化操作运行多次。k 均值算法的各种变体通常包括一些优化，例如选择多个运行中的最佳运行的同时，还将质心限制在数据集的成员(k-中心点算法)，选择中值(k-中心聚类)，减少对于初始中心的随机选择(k-means++)或允许模糊聚类分配(模糊c-均值)。

大部分k-均值类型算法需要预先指定集群数量–k ，这被认为是这些算法的最大缺点之一。此外，这些算法更适合大小近似的聚类，因为它们总是将对象分配到最近的质心。这导致聚类边界经常被错误地切割(这并不奇怪，因为该算法优化聚类中心，而不是聚类边界)。

K-均值算法有许多有趣的理论性质。首先，它将数据空间划分成一个沃罗诺伊图的结构。其次，它在概念上接近最近邻分类，因此在机器学习中很流行。第三，它可以被看作是基于模型的聚类的变体，劳埃德算法是下面讨论的该模型的期望最大化算法的变体。

• ''k''-均值聚类举例
• 
• k 均值算法将数据分离到Voronoi单元中，该单元假设聚类大小相同（此图不满足假设）

• 

• k 均值算法不能用于表示基于密度的聚类

2.3 基于分布的聚类

与统计最密切相关的聚类模型是以分布模型为基础的。聚类很容易被定义为最有可能属于同一分布的对象。这种方法的一个方便的特性是，它非常类似于人造数据集的生成方式:从一个分布中采取随机对象作为样本。

虽然这些方法的理论基础很好，但是，除非我们去限制模型的复杂性，不然它们就会遇到一个称为过拟合的关键问题。一个更复杂的模型通常能够更好地解释数据，这使得选出合适的模型复杂性这件事本身就是困难的。

有一种效果突出的方法被称为高斯混合模型(使用期望最大化算法)。在这里，数据集通常以固定(避免过拟合)数量的高斯分布建模，这些高斯分布被随机初始化，并且其参数被迭代优化以更好地适应数据集。这将收敛到局部上的最优解，所以多次运行可能会产生不同的结果。为了获得硬聚类，对象通常被分配到它们最可能属于的高斯分布；对于软集群，这不是必需的。

基于分布的聚类产生了复杂的聚类模型，可以捕捉属性之间的相关性和依赖性。然而，这些算法给用户带来了额外的负担:对于许多真实数据集，可能没有简明定义的数学模型(例如，假设高斯分布是一个对数据的相当强的假设)。

 

• 高斯混合模型聚类举例

 

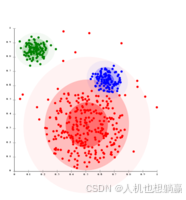
在高斯分布的数据上，EM的运行效果很好，因为它使用了高斯方法对聚类进行建模 

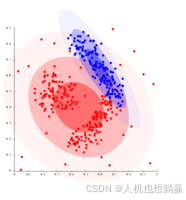
基于密度的聚类不能使用高斯分布来建模

2.4 基于密度的聚类

在基于密度的聚类中，[9] 聚类被定义为密度高于数据集其余部分的区域。这些稀疏区域中的对象——这些对象需要去分离聚类——通常被认为是噪声和边界点。

最受欢迎的[10] 基于密度的聚类方法是DBSCAN。[11] 与许多更新的方法相比，它具有一个被称为“密度可达性”的定义明确的聚类模型。类似于基于链接的聚类，它基于特定距离阈值内的连接点。但是，它只连接满足密度标准的点，在原始变体中定义为该半径内的最小数量的其他对象。一个集群由所有密度连接的对象(与许多其他方法不同，它可以形成任意形状的集群)加上这些对象范围内的所有对象组成。DBSCAN的另一个有趣的特性是它的复杂性相当低——它需要在数据库上进行线性数量的范围查询——并且它将在每次运行中发现本质上相同的结果(它对于核心点和噪声点是确定性的算法，但对于边界点不是)，因此不需要多次运行它。OPTICS [12] 是DBSCAN的一个归纳，它不需要为范围参数   选择合适的值，并且它会产生与链接聚类相关的分层结果。DeLi-Clu，[13] 即密度-链接-聚类算法结合了单链接聚类和OPTICS的思想，完全消除了    参数，并通过使用R树索引提供优于OPTICS的性能改进。

DBSCAN和OPTICS的主要缺点是它们期望由某种密度的下降来检测聚类边界。例如，在重叠高斯分布的数据集上——人工数据中的一个常见用例——这些算法产生的聚类边界通常看起来是任意的，因为聚类密度会不断降低。在由高斯混合模型组成的数据集上，诸如EM聚类等能够精确建模这种数据的方法几乎总是优于这些算法。

均值漂移是一种聚类方法，根据核密度估计，在这个运行的算法之下，每个对象将被移动到其附近密度最大的区域。最终，对象会收敛到密度的局部最大值。类似于k-均值聚类，这些“密度吸引子”可以作为数据集的代表，但是均值漂移可以检测类似于DBSCAN的任意形状的聚类。由于具有昂贵成本的迭代过程和密度估计，均值漂移通常比DBSCAN或k均值算法慢。此外，均值漂移算法对多维数据的适用性会受到核密度估计不平滑行为的阻碍，这导致了簇尾的过度分裂。[13]

• 基于密度的聚类举例

 

基于密度的DBSCAN聚类

 

OPTICS是一种DBSCAN变体，改进了对不同密度集群的处理

2.5 聚类分析的应用场景

（1） 商业应用

商业数据分析师通过聚类将用户根据其性质分类，从而发现不同的客户群，并且通过购买模式刻画不同的客户群特征，以便后期对不同客户群定制商业策略。

（2）计算生物学

生物学家使用聚类分析大量的动植物的基因遗传信息，从而获取更加准确的生物分类。

（3）电子商务

聚类分析在电子商务领域主要用于挖掘具有相似浏览行为的客户，并分析客户的共同特征，从而帮助电商运营者了解自己的客户，向客户提供更合适的服务。

总结

聚类分析，数据挖掘与机器学习领域的瑰宝，凭借其揭示数据集内在结构与模式的能力，成为决策制定的得力助手。其基本原理基于数据点间的相似性度量，通过算法自动将数据分组，使得同组内数据点彼此相似，而不同组的数据点则差异显著。这一过程无需预定义类别，让数据自身“说话”，发现潜在的群体和模式。

在方法层面，聚类分析涵盖了从K-means、层次聚类到DBSCAN等多种算法，每种方法都有其独特优势，适用于不同场景。K-means算法以簇内点到簇中心距离的平方和最小化为目标，适合处理大规模数据集；层次聚类则通过构建树状结构，展现数据集的层次性；而DBSCAN则能有效识别任意形状的簇，并对噪声数据进行处理。

应用场景方面，聚类分析广泛应用于市场营销、生物信息学、社交网络分析等领域。在市场营销中，通过客户细分，企业能更精准地定位目标客户群，制定个性化营销策略；在生物信息学中，聚类分析帮助科研人员识别基因表达模式，揭示生物过程的奥秘；在社交网络分析中，它有助于识别用户群体，理解信息传播机制。

展望未来，随着数据科学和机器学习技术的飞速发展，聚类分析将不断优化算法，提升效率与准确性，并在更多领域展现其强大价值。无论是初学者还是资深从业者，深入理解聚类分析的基本原理与方法，都将为数据驱动的决策制定提供有力支持，推动各行各业向智能化、精准化方向发展。