力扣心得（四）--回溯：组合总和

今天写的是力扣低216题，组合总和|||（不会打）

来看题干：在数字1~9中找出所有相加之和为 n 的 k 个数的组合（元素不可重复使用）

这是一个组合问题 ==> 回溯

回溯的步骤如下：（具体的可以看我发的力扣心得（三））

1.声明全局变量，写操作函数的大纲

#include <stdlib.h>
static int** ans;    // 结果数组（二维数组）
static int* ansSize; // 储存结果数组指针长度的数组
static int* path;    // 路径数组
static int pathTop;  // 路径数组当前长度
static int ansTop;   // 结果数组当前长度

void backtracking()
{

}

int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes) {
    // 1.申请内存
    ans = (int**)malloc(1000 * sizeof(int*));
    ansSize = (int*)malloc(1000 * sizeof(int));
    path = (int*)malloc(k * sizeof(int));

    // 2.初始化参数
    ansTop = 0;
    pathTop = 0;

    // 3.进入递归
    void backtracking()

    // 4.返回参数
    *returnSize = ansTop;
    *returnColumnSizes = ansSize;

    // 5.返回结果
    return ans;
}

2.画树形结构图

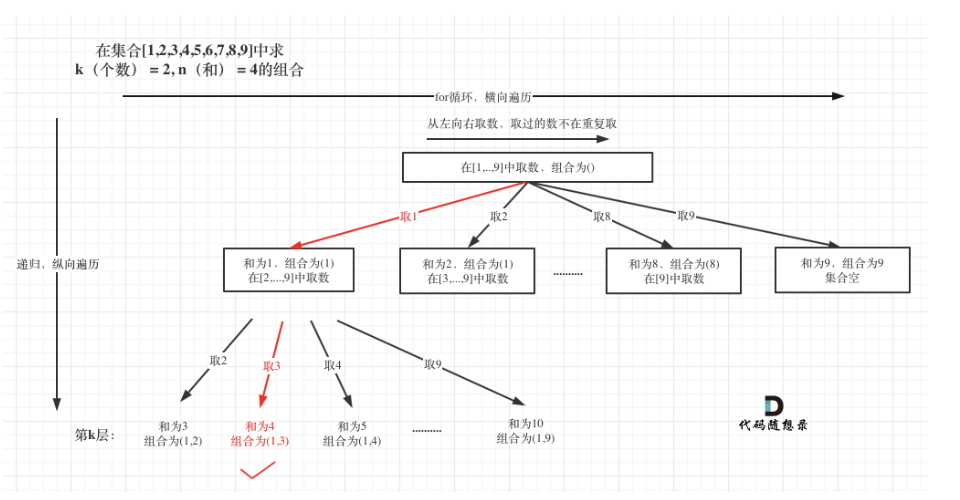
3.找终止条件和结构储存条件

看树状图：

终止条件：路径数达到k

储存条件：路径数总和为n

4.开始写递归函数

先来定参数：

1.肯定得有k和n和路径总和，不然无法写终止和存储条件
2.得有index，不然不知道现在遍历到哪个数了
那for 循环呢
我们的起点是目前遍历的数，也就是index【所以 i = index】
其次，我们的终点是数字9【所以是i <= 9】
最后，我们是要一个数一个数的遍历【所以是i++】
okok，那代码基本已经出来了

void backtracking(int k, int n, int sum, int index)
{
    // 终止条件：路径长度为k
    if (pathTop == k)
    {
        // 储存条件：路径总和为n
        if (sum == n)
        {
            // 因为我们要把满足条件的路径复制到返回数组中，所以要先申请内存（长度就是路径数组的长度）
            ans[ansTop] = (int*)malloc(pathTop * sizeof(int));
            for (int i = 0; i < pathTop; i++)
            {
                ans[ansTop][i] = path[i];
            }
            // 更新ansSize和ansTop的数据
            ansSize[ansTop++] = pathTop;
        }
        // 最后别忘记return
        return;
    }

    for (int i = index; i <= 9; i++)
    {
        // 把遍历到的数放入路径数组
        path[pathTop++] = i;
        sum += i;
        // 进入递归
        backtracking(k, n, sum, i + 1);
        // 撤回选择，恢复现场
        pathTop--;
        sum -= i;
    }
}

最后把操作函数中的递归部分补齐即可

int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes) {
    // 1.申请内存
    ans = (int**)malloc(1000 * sizeof(int*));
    ansSize = (int*)malloc(1000 * sizeof(int));
    path = (int*)malloc(k * sizeof(int));

    // 2.初始化参数
    ansTop = 0;
    pathTop = 0;

    // 3.进入递归（就动了这里的参数）
    backtracking(k, n, 0, 1);

    // 4.返回参数
    *returnSize = ansTop;
    *returnColumnSizes = ansSize;

    // 5.返回结果
    return ans;
}

来看看完整代码

#include <stdlib.h>

static int** ans;    // 结果数组（二维数组）
static int* ansSize; // 储存结果数组指针长度的数组
static int* path;    // 路径数组
static int pathTop;  // 路径数组当前长度
static int ansTop;   // 结果数组当前长度

void backtracking(int k, int n, int sum, int index)
{
    // 终止条件：路径长度为k
    if (pathTop == k)
    {
        // 储存条件：路径总和为n
        if (sum == n)
        {
            // 因为我们要把满足条件的路径复制到返回数组中，所以要先申请内存（长度就是路径数组的长度）
            ans[ansTop] = (int*)malloc(pathTop * sizeof(int));
            for (int i = 0; i < pathTop; i++)
            {
                ans[ansTop][i] = path[i];
            }
            // 更新ansSize和ansTop的数据
            ansSize[ansTop++] = pathTop;
        }
        // 最后别忘记return
        return;
    }

    for (int i = index; i <= 9; i++)
    {
        // 把遍历到的数放入路径数组
        path[pathTop++] = i;
        sum += i;
        // 进入递归
        backtracking(k, n, sum, i + 1);
        // 撤回选择，恢复现场
        pathTop--;
        sum -= i;
    }
}

int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes) {
    // 1.申请内存
    ans = (int**)malloc(1000 * sizeof(int*));
    ansSize = (int*)malloc(1000 * sizeof(int));
    path = (int*)malloc(k * sizeof(int));

    // 2.初始化参数
    ansTop = 0;
    pathTop = 0;

    // 3.进入递归
    backtracking(k, n, 0, 1);

    // 4.返回参数
    *returnSize = ansTop;
    *returnColumnSizes = ansSize;

    // 5.返回结果
    return ans;
}

提交！