飞蛾扑火算法（MFO）优化支持向量机原理及MATLAB代码复现

0 引言

飞蛾扑火算法（Moth flame optimization）是由Seyedali Mirjalili在2015年基于飞蛾对光源飞行的策略提出的群体智能算法，该算法主要模拟了飞蛾围绕光源螺旋飞行的过程。

1 数学模型

MFO算法数学模型建模围绕飞蛾扑火三个阶段进行模型构建，分别是选择火焰、飞蛾围绕火焰飞行及飞行扑火的行为，具体模型构建如下：

1）初始化定义飞蛾和火焰：在MFO算法飞蛾表示问题优化的解，火焰为飞行当前所能找到最优解，故飞蛾和火焰均以问题维度进行初始化生成初始化变量，具体如下：

式中M为飞蛾个体，其中n为飞蛾个体数目，d为问题维度；OM为飞蛾的适应度；F为火焰位置，其维度及个数于飞蛾相同，OF为火焰的适应度。

2）飞蛾扑火的飞行行为：飞蛾在不断搜索空间内个体，而火焰为最佳个体位置，飞蛾是围绕火焰进行螺旋递进过程，其表达过程如下：

式中S为螺旋函数，D为飞蛾和火焰之间位置，b是定义对数螺旋形状的一个常数，t是[-1,1]中的一个随机数。其飞行过程如下图所示

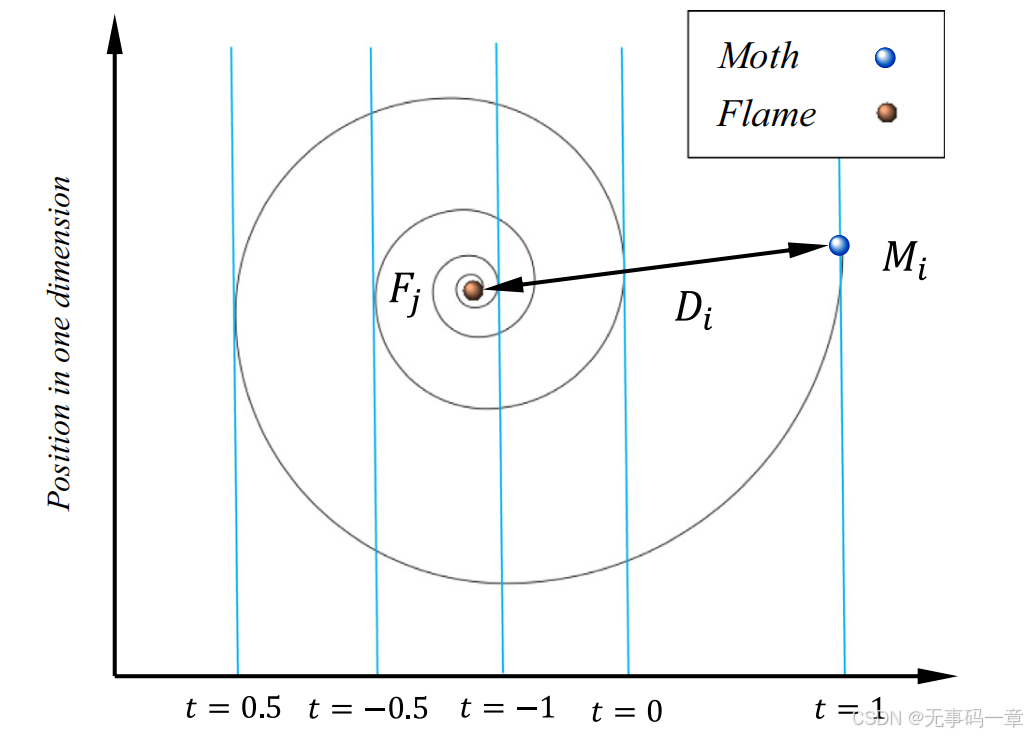
3）定义下一代飞蛾和火焰：将飞行后飞蛾个体进行更新，将其优势作为下一迭代火焰模拟，迭代上述过程。

2 优化方式

前篇对支持向量机（支持向量机原理及Matlab代码-CSDN博客）原理讲解，从支持向量机模型运算过程中，可以了解到模型高维映射核函数参数g和处罚因子c对模型预测结果影响最为重要。因此结合上述MFO原理介绍，可以将支持向量机的超参数作为飞蛾和火焰个体位置，每一个种群位置对应支持向量机的预测值，将这个预测值作为适应度区分飞蛾和火焰，模拟飞蛾对火焰的螺旋飞行策略，更新飞蛾个体，进行下一迭代飞蛾扑火。

3 MATLAB代码

3.1 伪代码

3.2 MFO主函数代码

while Iteration<Max_iteration+1
    
    % 火焰数量 Eq. (3.14) 
    Flame_no=round(N-Iteration*((N-1)/Max_iteration));
    
    for i=1:size(Moth_pos,1)
        
        % 飞蛾位置边界
        Flag4ub=Moth_pos(i,:)>ub;
        Flag4lb=Moth_pos(i,:)<lb;
        Moth_pos(i,:)=(Moth_pos(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;  
        
        % 对应适应度计算
        Moth_fitness(1,i)=SYD(Moth_pos(i,:),net);  
        net.trainParam.showWindow = 0;  
    end
       
    if Iteration==1
        % 第一批飞蛾分类
        [fitness_sorted I] = sort(Moth_fitness);
        sorted_population=Moth_pos(I,:);
        
        % 更新火焰
        best_flames=sorted_population;
        best_flame_fitness=fitness_sorted;
    else
        
        % 剩下飞蛾分类
        double_population=[previous_population;best_flames];
        double_fitness=[previous_fitness best_flame_fitness];
        
        [double_fitness_sorted I]=sort(double_fitness);
        double_sorted_population=double_population(I,:);
        
        fitness_sorted=double_fitness_sorted(1:N);
        sorted_population=double_sorted_population(1:N,:);
        
        % 更新对应火焰
        best_flames=sorted_population;
        best_flame_fitness=fitness_sorted;
    end
    
    % 更新目前获得的最佳火焰位置
    Best_flame_score=fitness_sorted(1);
    Best_flame_pos=sorted_population(1,:);
      
    previous_population=Moth_pos;
    previous_fitness=Moth_fitness;
    
    %Eq. (3.12)
    a=-1+Iteration*((-1)/Max_iteration);
    
    for i=1:size(Moth_pos,1)
        
        for j=1:size(Moth_pos,2)
            if i<=Flame_no % 更新飞蛾相对于相应火焰的位置
                
                % Eq. (3.13)
                distance_to_flame=abs(sorted_population(i,j)-Moth_pos(i,j));
                b=1;
                t=(a-1)*rand+1;
                
                % Eq. (3.12)
                Moth_pos(i,j)=distance_to_flame*exp(b.*t).*cos(t.*2*pi)+sorted_population(i,j);
            end
            
            if i>Flame_no % 将飞蛾的位置与一个火焰相对比
                
                % Eq. (3.13)
                distance_to_flame=abs(sorted_population(i,j)-Moth_pos(i,j));
                b=1;
                t=(a-1)*rand+1;
                
                % Eq. (3.12)
                Moth_pos(i,j)=distance_to_flame*exp(b.*t).*cos(t.*2*pi)+sorted_population(Flame_no,j);
            end
            
        end
        
    end
    
    Convergence_curve(Iteration)=Best_flame_score;
    

    Iteration=Iteration+1; 
end

3.3 MFO-SVR、MFO-SVM

回归模型和分类模型的代码复现（飞蛾扑火算法优化支持向量机模型（MFO-SVM））