基于鲸鱼优化算法 优化 VMD（变分模态分解）

已于 2025-04-05 07:21:30 修改
阅读量959 收藏
点赞数 16
文章标签： 算法
于 2025-04-05 07:10:46 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2401_86822270/article/details/147005595
版权

基于 鲸鱼优化算法 (Whale Optimization Algorithm, WOA) 优化 VMD（变分模态分解）参数 K 和 α 的 Python 实现。

文章目录


WOA 是一种元启发式优化算法，可用于寻找最优的 VMD 参数组合。

1. 安装依赖

确保安装了必要的库：

pip install numpy scipy matplotlib scikit-learn

在这里插入图片描述

2. 鲸鱼优化算法 (WOA) 核心code

WOA 的核心实现代码：

import numpy as np
from scipy.optimize import minimize

# WOA 算法实现
def whale_optimization_algorithm(objective_func, lb, ub, dim, search_agents=30, max_iter=100):
    # 初始化种群
    X = np.random.uniform(lb, ub, (search_agents, dim))
    best_position = np.zeros(dim)
    best_score = float('inf')

    for t in range(max_iter):
        a = 2 - t * (2 / max_iter)  # 线性递减参数 a
        for i in range(search_agents):
            # 计算适应度
            fitness = objective_func(X[i])
            if fitness < best_score:
                best_score = fitness
                best_position = X[i]

            # 更新位置
            r1 = np.random.rand()
            r2 = np.random.rand()
            A = 2 * a * r1 - a
            C = 2 * r2
            b = 1  # 螺旋形状参数
            l = np.random.uniform(-1, 1)

            p = np.random.rand()
            if p < 0.5:
                if abs(A) < 1:
                    D = abs(C * best_position - X[i])
                    X[i] = best_position - A * D
                else:
                    rand_leader_index = np.random.randint(0, search_agents)
                    X_rand = X[rand_leader_index]
                    D_X_rand = abs(C * X_rand - X[i])
                    X[i] = X_rand - A * D_X_rand
            else:
                D_best = abs(best_position - X[i])
                X[i] = D_best * np.exp(b * l) * np.cos(2 * np.pi * l) + best_position

            # 边界处理
            X[i] = np.clip(X[i], lb, ub)

    return best_position, best_score

3. VMD 模态分解与目标函数

VMD 的目标是通过优化参数 K 和 α 来最小化重构误差或其他指标。我们使用 scipy 中的 minimize 函数来辅助优化，并定义目标函数。

from vmdpy import VMD  # 需要安装 vmdpy 库：pip install vmdpy

# 目标函数：基于 VMD 的重构误差
def objective_function(params, signal):
    K, alpha = params
    K = int(K)  # 模态数量必须为整数
    alpha = max(0, alpha)  # 确保 α 为正数

    # 执行 VMD 分解
    try:
        u, u_hat, omega = VMD(signal, alpha=alpha, tau=0, K=K, DC=0, init=1, tol=1e-7)
        reconstructed_signal = np.sum(u, axis=0)  # 重构信号
        error = np.mean((signal - reconstructed_signal) ** 2)  # 均方误差
    except Exception:
        error = float('inf')  # 如果参数无效，返回极大值

    return error

在这里插入图片描述

4. 主程序：结合 WOA 和 VMD

xiamianzhege市 主程序，结合 WOA 和 VMD 进行参数优化：

import numpy as np
import matplotlib.pyplot as plt

# 示例信号
def generate_signal():
    t = np.linspace(0, 1, 500)
    signal = np.sin(2 * np.pi * 50 * t) + 0.5 * np.sin(2 * np.pi * 120 * t)  # 合成信号
    return t, signal

if __name__ == "__main__":
    # 生成信号
    t, signal = generate_signal()

    # 定义搜索空间
    lb = [2, 0.1]  # K 和 α 的下界
    ub = [10, 5000]  # K 和 α 的上界
    dim = 2  # 参数维度 (K 和 α)

    # 使用 WOA 优化 VMD 参数
    def wrapper(params):
        return objective_function(params, signal)

    best_params, best_score = whale_optimization_algorithm(
        objective_func=wrapper,
        lb=lb,
        ub=ub,
        dim=dim,
        search_agents=20,
        max_iter=50
    )

    # 输出优化结果
    K_optimal, alpha_optimal = int(best_params[0]), best_params[1]
    print(f"Optimal K: {K_optimal}, Optimal Alpha: {alpha_optimal:.2f}")
    print(f"Best Objective Score: {best_score:.4f}")

    # 使用最优参数进行 VMD 分解
    u, u_hat, omega = VMD(signal, alpha=alpha_optimal, tau=0, K=K_optimal, DC=0, init=1, tol=1e-7)

    # 可视化结果
    plt.figure(figsize=(10, 6))
    plt.subplot(2, 1, 1)
    plt.plot(t, signal, label="Original Signal")
    plt.title("Original Signal")
    plt.legend()

    plt.subplot(2, 1, 2)
    for i in range(K_optimal):
        plt.plot(t, u[i], label=f"IMF {i+1}")
    plt.title("VMD Decomposition")
    plt.legend()
    plt.show()

5. 结果说明

  1. 优化过程：

    • WOA 会根据目标函数（如均方误差）调整 K 和 α 的值。
    • 最终输出优化后的 K 和 α 参数。

  2. VMD 分解：

    • 使用优化后的参数对信号进行 VMD 分解，得到多个固有模态函数（IMFs）。
    • 可视化原始信号和分解后的 IMFs。

6. 注意

  1. 参数范围：

    • K 的取值范围通常在 [2, 10] 之间。
    • α 的取值范围可以根据信号特性调整。

  2. 目标函数：

    • 可根据具体需求修改目标函数，例如使用其他性能指标（如能量熵、频谱误差等）。

  3. 计算效率：

    • VMD 的计算复杂度较高，建议在小规模数据集上测试。

以上代码仅供参考。

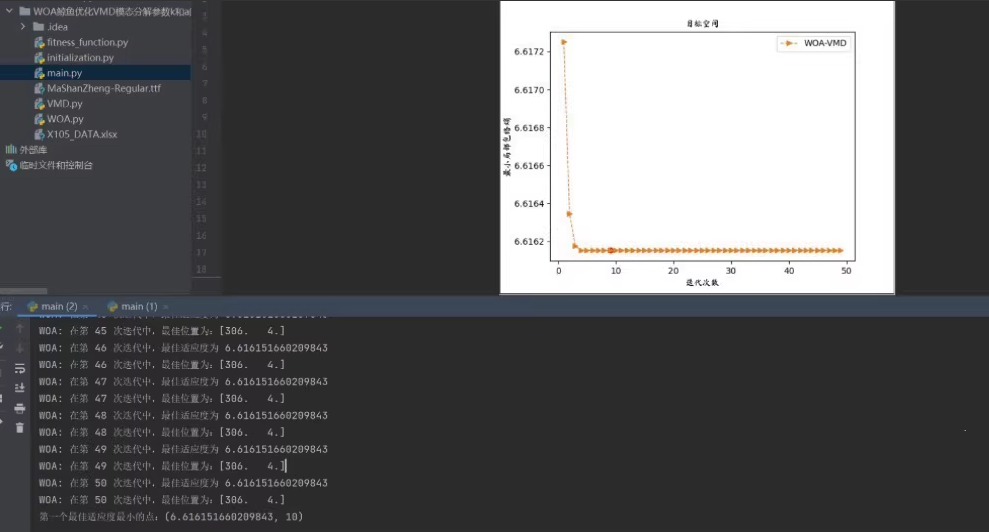
使用鲸鱼优化算法（WOA）来优化VMD参数的Python项目。，图表展示了迭代次数与目标函数值的关系。

完整的代码示例，包括如何运行这个项目以及如何生成类似的图表。

仅供参考。

1. 安装依赖

确保安装了必要的库：

pip install numpy scipy matplotlib vmdpy

2. 主要文件结构

假设你的项目文件结构如下：

- WOA.py
- VMD.py
- fitness_function.py
- main.py

3. 各个文件的内容

WOA.py - 鲸鱼优化算法实现
import numpy as np

def whale_optimization_algorithm(objective_func, lb, ub, dim, search_agents=30, max_iter=100):
    # 初始化种群
    X = np.random.uniform(lb, ub, (search_agents, dim))
    best_position = np.zeros(dim)
    best_score = float('inf')
    scores = []

    for t in range(max_iter):
        a = 2 - t * (2 / max_iter)  # 线性递减参数 a
        for i in range(search_agents):
            # 计算适应度
            fitness = objective_func(X[i])
            if fitness < best_score:
                best_score = fitness
                best_position = X[i]

            # 更新位置
            r1 = np.random.rand()
            r2 = np.random.rand()
            A = 2 * a * r1 - a
            C = 2 * r2
            b = 1  # 螺旋形状参数
            l = np.random.uniform(-1, 1)

            p = np.random.rand()
            if p < 0.5:
                if abs(A) < 1:
                    D = abs(C * best_position - X[i])
                    X[i] = best_position - A * D
                else:
                    rand_leader_index = np.random.randint(0, search_agents)
                    X_rand = X[rand_leader_index]
                    D_X_rand = abs(C * X_rand - X[i])
                    X[i] = X_rand - A * D_X_rand
            else:
                D_best = abs(best_position - X[i])
                X[i] = D_best * np.exp(b * l) * np.cos(2 * np.pi * l) + best_position

            # 边界处理
            X[i] = np.clip(X[i], lb, ub)

        scores.append(best_score)

    return best_position, best_score, scores
VMD.py - VMD 模态分解
from vmdpy import VMD

def vmd_decomposition(signal, K, alpha):
    u, u_hat, omega = VMD(signal, alpha=alpha, tau=0, K=K, DC=0, init=1, tol=1e-7)
    return u, u_hat, omega
fitness_function.py - 目标函数
import numpy as np

def objective_function(params, signal):
    K, alpha = params
    K = int(K)  # 模态数量必须为整数
    alpha = max(0, alpha)  # 确保 α 为正数

    try:
        u, u_hat, omega = vmd_decomposition(signal, K, alpha)
        reconstructed_signal = np.sum(u, axis=0)  # 重构信号
        error = np.mean((signal - reconstructed_signal) ** 2)  # 均方误差
    except Exception:
        error = float('inf')  # 如果参数无效，返回极大值

    return error
main.py - 主程序
import numpy as np
import matplotlib.pyplot as plt
from WOA import whale_optimization_algorithm
from fitness_function import objective_function
from VMD import vmd_decomposition

# 示例信号
def generate_signal():
    t = np.linspace(0, 1, 500)
    signal = np.sin(2 * np.pi * 50 * t) + 0.5 * np.sin(2 * np.pi * 120 * t)  # 合成信号
    return t, signal

if __name__ == "__main__":
    # 生成信号
    t, signal = generate_signal()

    # 定义搜索空间
    lb = [2, 0.1]  # K 和 α 的下界
    ub = [10, 5000]  # K 和 α 的上界
    dim = 2  # 参数维度 (K 和 α)

    # 使用 WOA 优化 VMD 参数
    def wrapper(params):
        return objective_function(params, signal)

    best_params, best_score, scores = whale_optimization_algorithm(
        objective_func=wrapper,
        lb=lb,
        ub=ub,
        dim=dim,
        search_agents=20,
        max_iter=50
    )

    # 输出优化结果
    K_optimal, alpha_optimal = int(best_params[0]), best_params[1]
    print(f"Optimal K: {K_optimal}, Optimal Alpha: {alpha_optimal:.2f}")
    print(f"Best Objective Score: {best_score:.4f}")

    # 使用最优参数进行 VMD 分解
    u, u_hat, omega = vmd_decomposition(signal, K_optimal, alpha_optimal)

    # 可视化结果
    plt.figure(figsize=(10, 6))
    plt.subplot(2, 1, 1)
    plt.plot(t, signal, label="Original Signal")
    plt.title("Original Signal")
    plt.legend()

    plt.subplot(2, 1, 2)
    for i in range(K_optimal):
        plt.plot(t, u[i], label=f"IMF {i+1}")
    plt.title("VMD Decomposition")
    plt.legend()
    plt.show()

    # 绘制迭代过程中的目标函数值
    plt.figure(figsize=(8, 6))
    plt.plot(scores, label="Objective Function Value")
    plt.xlabel("Iteration")
    plt.ylabel("Objective Function Value")
    plt.title("Convergence Curve")
    plt.legend()
    plt.show()

4. 运行项目

确保所有文件都在同一目录下，并且已经安装了所需的库。然后在命令行中运行：

python main.py

这将执行鲸鱼优化算法来优化VMD参数，并绘制原始信号和分解后的IMFs，以及收敛曲线。

WOA-VMD鲸鱼算法WOA优化VMD变分模态分解
04-19
### WOA-VMD鲸鱼算法优化VMD变分模态分解技术详解 #### 一、基础知识概述 **WOA-VMD鲸鱼算法优化VMD变分模态分解**是一种结合了鲸鱼优化算法(WOA)与变分模态分解(VMD)的方法，用于对复杂信号进行高效分解和分析的...
vmd可变分模态分解
12-26
此文件 能够VMD 法避免了发生混叠 现象，且运算效率更高，在低信噪比的情况下噪声 处理效果更好，有利于故障信号的特征提取
变分模态分解（VMD）-Python代码
枫的博客
04-23 2万+
Python实现变分模态分解——VMD
VMD分解python实现方法
晓林爱学习的博客
06-27 2825
本文将介绍VMD分解的原理及其在Python中的实现方法，并提供示例代码和案例应用。本文将介绍一个实际的案例应用，比如用于机械振动信号分析，通过VMD分解可以将复杂的振动信号分解为几个模态分量，从而实现故障诊断和预测。（3）第三方库PyVMD的使用：PyVMD是一个专门为VMD分解开发的Python库，提供了一套完整的VMD实现方法，包括信号预处理、VMD分解和结果分析。（1）基于NumPy和SciPy的VMD实现方法：使用NumPy进行信号预处理，然后利用SciPy中的优化函数来解决VMD的优化问题。
VMD模态分解以及K值优化python代码
李白白的博客
12-19 6266
看。其他的待补充完善。
python VMD分解及其程序
晓林爱学习的博客
06-27 1458
Python作为一种广泛应用的编程语言，提供了丰富的信号处理库和数值计算工具，可以方便地实现VMD分解算法。Variational Mode Decomposition（VMD）是一种强大的信号处理技术，用于将非平稳信号分解为一组时频分量，称为模态。VMD分解是通过优化问题来实现的，其目标是将非平稳信号分解为一组模态分量，每个模态分量具有不同的频率和振幅特征。VMD分解在许多领域都有广泛的应用。例如，它可用于机械振动信号分析，通过VMD分解将复杂的振动信号分解为几个模态分量，从而实现故障诊断和预测。
数字信号处理技术（二）变分模态分解（VMD）-Python代码
weixin_45063703的博客
05-18 3万+
研究方向是时间序列数据预测，采用的数据都是时间序列数据，本次实验的数据集是海浪高度数据信息。VMD可以很好的解决EMD 中出现的模态混叠现象，所以现在很多研究方向转向了VMD，利用其优点和其他的模型进行结合使用。VMD的子序列个数的选择，有些是根据模态混叠现象，有些是进行迭代寻优，有些是自己指定个数等等方式。
WOA-VMD鲸鱼优化算法WOA优化VMD变分模态分解，WOA-VMD信号分解 1.利用优化算法优化VMD中的参数k、a，适
02-01
WOA-VMD鲸鱼优化算法WOA优化VMD变分模态分解，WOA-VMD信号分解。 1.利用优化算法优化VMD中的参数k、a，适应度函数为包络熵。分解效果好，包含分解效果图、频率图、收敛曲线等图等。 2.附赠测试数据 直接运行main...
鲸鱼算法(WOA)优化变分模态分解(VMD)参数python
04-28
变分模态分解（Variational Mode Decomposition, VMD）是信号处理领域的一种非线性、无监督的时间序列分析方法，由Eckart Abdenur和Dragomir Jovanovic于2011年提出。VMD旨在将复杂信号分解为一系列具有固定频率的...
Matlab实现WOA-VMD鲸鱼算法WOA优化VMD变分模态分解（完整源码和数据)
04-14
Matlab实现WOA-VMD鲸鱼算法WOA优化VMD变分模态分解（完整源码和数据) 1.利用鲸鱼优化算法优化vmd中的参数k、a，分解效果好，包含边际谱、频率图、收敛曲线等图，满足您的需求，使用者较少，适合作为创新点。 2.包含...
【MATLAB, 可运行】鲸鱼优化算法优化VMD变分模态分解MATLAB程序代码 - 惩罚系数和分解模态数优化代码
03-10
鲸鱼优化算法优化VMD变分模态分解matlab代码，亲测可用。本人添加注释清楚。可以直接运行出结果图像，使用的EXCEL数据，可以换自己的数据运行。 1.【目标函数】各IMF分量的包络熵局部极小值 2.【优化变量】VMD方法的...
变分模态分解（VMD）python代码及其测试用例
02-26
变分模态分解（VMD）可以实现信号频域内各个分量的自适应分割，但需要指定模态个数K等参数。
灰狼算法优化变分模态分解（VMD）参数python
04-27
1.python程序 2.有数据集，可直接运行
Vmd的分解代码
10-29
信号分解，地震资料分解，都非常实用，而且是可以用的
vmd，python实现代码
11-07
根据https://www.cnblogs.com/xingshansi/p/6511916.html分享的matlab代码改编
变分模态分解（VMD）
热门推荐
weixin_44225962的博客
09-07 3万+
变分模态分解（VMD）前言一、VMD [^1]是什么？基本概念求解步骤二、python实现引入vmdpy库变分模态分解（VMD）-Python代码三、补充EMD库--pyemdEMD与VMD区别尝试后继续补充 前言 在信号处理中，变分模态分解是一种信号分解估计方法。该方法在获取分解分量的过程中通过迭代搜寻变分模型最优解来确定每个分量的频率中心和带宽，从而能够自适应地实现信号的频域剖分及各分量的有效分离。 一、VMD 1是什么？ 基本概念 VMD（Variational mode decompositi
基于VMD变分模态分解算法Python程序
黑科技小土豆的博客
03-01 2456
基于VMD变分模态分解算法Python程序
vmd变分模态分解 Python
最新发布
03-21
<think>好的，我现在需要回答用户关于VMD（变分模态分解）在Python中的应用的问题。首先，我要确保自己正确理解VMD的概念和原理，然后了解如何在Python中实现它。 首先，VMD是什么？变分模态分解是一种信号处理技术，用于将非平稳信号分解成多个固有模态函数（IMFs），也称为模态。它通过解决变分优化问题来同时确定所有模态的中心频率和带宽。与EMD（经验模态分解）相比，VMD基于变分框架，具有更好的数学基础和抗噪声能力。 接下来，我需要回忆VMD的基本步骤。VMD的主要步骤包括构建变分问题，引入拉格朗日乘子法求解，使用交替方向乘子法（ADMM）迭代更新模态和中心频率。关键点在于每个模态的带宽估计和中心频率的更新。 然后，用户想知道如何在Python中使用VMD。我需要检查是否有现有的Python库支持VMD。记得有一个叫做vmdpy的库，或者可能需要自己实现。但不确定这个库的可靠性，或者是否有其他实现方式。此外，可能还有其他开源实现，比如GitHub上的某些项目，但用户可能需要安装这些库或者参考代码。 需要验证是否存在vmdpy库。可以快速搜索一下，假设存在的话，用户需要安装它，可能通过pip install vmdpy。然后，导入该库中的VMD函数，准备输入信号，设置参数，如模态数K、alpha（平衡参数）、tau（时间步长）等，然后调用函数得到分解后的模态。 同时，可能需要解释参数的选择，比如K的选择影响分解的模态数量，alpha控制带宽，tau可能与收敛速度有关。还要注意信号的长度，是否需要是偶数，或者进行预处理。 此外，如果vmdpy不可用，用户可能需要手动实现VMD算法。这时候需要数学推导，比如构建变分问题，使用ADMM迭代更新。这部分可能比较复杂，涉及到傅里叶变换、频域更新等步骤。对于一般用户来说，推荐使用现有的库更为方便。 可能还需要给出一个示例代码，展示如何使用vmdpy进行分解，并绘制结果。例如，生成一个测试信号，包含多个频率成分，然后应用VMD分解，并可视化各个模态。 还需要注意常见问题，如参数选择不当导致的过分解或欠分解，收敛条件设置，计算复杂度等。可能建议用户通过试错法调整参数，或者参考相关文献中的参数设置。 最后，总结一下VMD的优势和应用场景，比如处理非平稳信号，噪声鲁棒性，适用于生物医学信号分析、机械故障诊断等领域。并提醒用户在使用时注意参数调整和结果验证。</think>以下是对VMD变分模态分解及其Python实现的介绍，分步说明清晰易懂： --- ### **1. VMD变分模态分解简介** **定义**： VMD（Variational Mode Decomposition）是一种自适应信号分解方法，通过构建变分优化问题将信号分解为多个窄带模态分量（IMF）。每个模态在频域具有稀疏性，且中心频率可自动确定。 **核心思想**： - 将信号分解为$K$个模态$u_k(t)$ - 最小化所有模态的带宽总和，约束条件为各模态之和等于原信号 - 数学表达： $$ \min_{\{u_k\},\{\omega_k\}} \sum_{k=1}^K \left\| \partial_t \left[ (\delta(t) + \frac{j}{\pi t}) * u_k(t) \right] e^{-j\omega_k t} \right\|_2^2 \quad \text{s.t.} \quad \sum_{k=1}^K u_k = f(t) $$ --- ### **2. Python实现步骤** #### **(1) 安装库** 推荐使用`vmdpy`库，需提前安装： ```bash pip install vmdpy ``` #### **(2) 导入库与生成测试信号** ```python import numpy as np from vmdpy import VMD import matplotlib.pyplot as plt # 生成含多频率成分的测试信号 t = np.linspace(0, 1, 1000) f1 = 5 # 低频成分 f2 = 20 # 高频成分 signal = np.sin(2*np.pi*f1*t) + 0.5*np.sin(2*np.pi*f2*t) ``` #### **(3) 设置参数并分解** ```python alpha = 2000 # 带宽约束参数（越大带宽越小） tau = 0. # 噪声容忍度 K = 2 # 分解模态数 DC = 0 # 是否包含直流分量 init = 1 # 初始化中心频率方式 tol = 1e-7 # 收敛阈值 # 执行VMD分解 u, u_hat, omega = VMD(signal, alpha, tau, K, DC, init, tol) ``` #### **(4) 可视化结果** ```python plt.figure(figsize=(12, 6)) for i in range(K): plt.subplot(K+1, 1, i+1) plt.plot(t, u[i,:], linewidth=0.5) plt.ylabel(f'IMF {i+1}') plt.subplot(K+1, 1, K+1) plt.plot(t, signal, 'r', linewidth=0.5) plt.ylabel('Original Signal') plt.tight_layout() plt.show() ``` --- ### **3. 关键参数说明** | 参数 | 作用 | 典型值 | |---------|----------------------------------|----------------| | `K` | 分解模态数量 | 根据信号复杂度 | | `alpha` | 控制模态带宽（越大越窄） | 1000~3000 | | `tau` | 噪声抑制能力（0为严格约束） | 0~1 | | `tol` | 迭代收敛阈值 | 1e-6~1e-7 | --- ### **4. 常见问题** - **如何选择K值？** 通过观察频谱或试错法，确保模态间频率不重叠。 - **分解结果不理想？** 调整`alpha`和`K`，或对信号进行去噪预处理。 --- ### **5. 应用场景** - 机械振动信号分析（轴承故障检测） - 生物医学信号处理（EEG/ECG分解） - 金融时间序列去噪 --- ### **6. 扩展阅读** - 论文：[Variational Mode Decomposition (Dragomiretskiy et al., 2014)](https://doi.org/10.1109/TSP.2013.2288675) - GitHub库：[vmdpy](https://github.com/vrcarva/vmdpy)
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值