机器学习(3-2)：逻辑回归【分类(Classification)】之二——二分类

逻辑回归的模型

希望： 

3.2.1 假说表示(Hypothesis Representation)

由于逻辑回归要求我们的输出值在 0 和 1 之间，因此我们需要有一个满足 的假设函数：

其中， 为特征向量，  为逻辑函数，也叫做S形函数（Sigmoid Function）或者叫做逻辑函数(Logistic Function)，它具体为：

逻辑函数在图像上具体是这样子的：

不难看出逻辑函数左侧无限趋近 0，右侧无限趋近 1，这正符合我们所需要的模型的输出值介于 0 和 1 之间。

讲上面两个式子结合一下，我们的假设函数也可以写作：

的作用是，根据设定的参数，输入给定的变量，计算输出变量的值为 1 的可能性（Estimated Probably），即 ：

由概率定义知：

因此：

假设 ，表示 y 属于正向类的可能性为 70% ，所以 y=0  的概率为 30%  。

3.2.2 决策界限(Decision Boundary)

可以更好地理解逻辑回归中的假设函数的作用。

逻辑函数在图像上具体是这样子的：

不难看出逻辑函数左侧无限趋近 0，右侧无限趋近 1，这正符合我们所需要的模型的输出值介于 0 和 1 之间。

如果我们预测：如果h  如果 即：

1. 当 时， ，  y=1 ；
2. 当 时， ，  y=0 ；

于是 就成了决策边界。

决策边界（Decision Boundary）由假设函数决定，理论上可以为任意曲线，也就是说根据模型计算得到的值再由决策边界进行决定最终属于正向类还是负向类。

例子：线性决策边界

假设函数：

逻辑函数：

参数： ，  ，

预测：当 即  时，模型预测 y = 1 。

           当 即  时，模型预测 y = 0 。

决策边界： ，将预测值为 1 和 0 的两个区域区分开来。

例子：非线性决策边界

还有更加复杂的情况，如果数据像这样分布呢：

则需要曲线才能将两个类区分开来，就需要用到二次方，如：

假设函数：

逻辑函数：

参数假设为： ，  ，

预测：当 即  时，模型预测 。

         当 即  时，模型预测  。。

决策边界： ，则曲线正好是以原点为圆心，1 为半径的圆。将预测值为 1 和 0 的两个区域区分开来。

我们可以用任意复杂的曲线作为分布复杂的数据的决策边界。

3.2.3 代价函数(Cost Fuction)

训练集(Training Set)：

m个样本：

假设函数：

决策边界：

问题：如何选择参数 呢？

这就涉及到了逻辑回归的拟合问题。

定义

由线性回归的代价函数：

若我们定义：

则有：

称 为逻辑回归的单样本代价函数

称 为逻辑回归的代价函数，

我们将+ 代入代价函数，则有：

该函数是个非凸函数，这会导致在梯度下降时没有全局最优解。于是我们必须另外选择一个代价函数。如：

这个函数看起来很复杂，但画出图形如下：

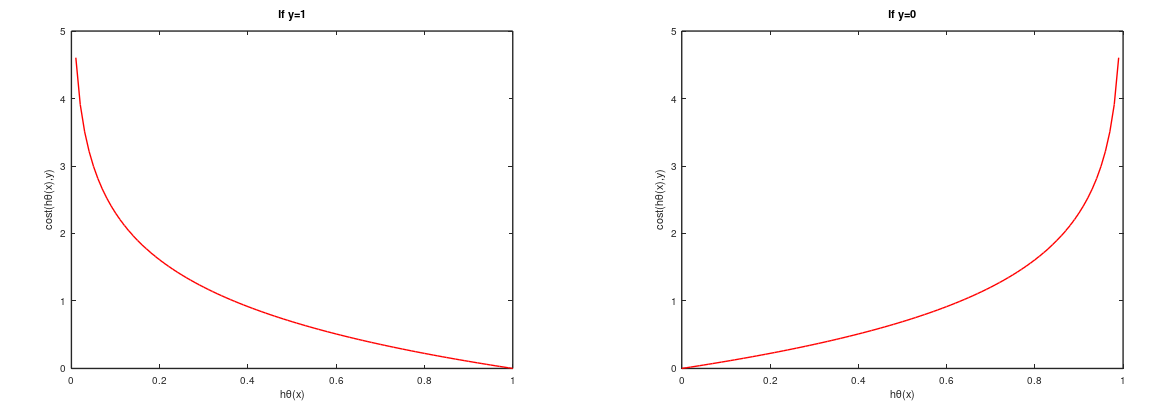
通过上面图形，我们知道：

预测：如果  ,预测y=1 ，此时Cost=0    。(正常预测)

          如果 ,预测y=1 ，此时Cost=0.8 。(正常预测)

          如果 ,预测y=1 ，此时Cost→∞  。(极不正常预测)

反之：如果  ,预测y=0 ，此时Cost→∞  。(极不正常预测)

          如果 ,预测y=0 ，此时Cost=1   。(可疑预测，因为Cost比预测y=1大)

          如果  ,预测y=0 ，此时Cost=0    。(正常预测)

 上述图形用Octave绘制的代码如下：

clear;clc；close;
x=[0:0.01:1];
y1=-log(x);
% 绘制第一个子图
subplot(1,2,1);
plot(x,y1,'r');
title('If y=1');x
label('hθ(x)');ylabel('cost(hθ(x),y)');
% 绘制第二个子图
y0=-log(1-x);
subplot(1,2,2);
plot(x,y0,'r');
title('If y=0');
xlabel('hθ(x)');
ylabel('cost(hθ(x),y)');

简化代价函数与梯度下降

逻辑回归的代价函数：

单样本代价函数：

注意：在逻辑回归中，y 只能取0或1。

简化代价函数

以上单样本代价函数是不连续的，我们将其合并为一个式子，这样我们可以更方便地写出单样本代价函数，且可以运用梯度下降。结果如下：

逻辑回归的代价函数

这个式子的来源于统计学中的极大似然法，这是一种快速寻找参数的方法。

梯度下降求参数θ

逻辑回归的代价函数：

找到合适的参数θ ：使得 最小。

选择一个合适输入特征x ,输出：   即

代价函数的偏导函数：

梯度下降寻找合适的参数θ ：重复迭代

观察 ，我们会惊人地发现形式上和以前的线性回归是一样的。

但是由于逻辑回归中假设函数和线性回归中的假设函数是不一样的：

1. 在线性回归中 ，
2. 逻辑回归中

所以梯度下降的算法是完全不一样的。但是控制逻辑是一样的。

高级优化

在梯度下降算法中，核心是计算 和 ，选择合适的步长α ，重复迭代

使得 极小。

为了提高逻辑回归的效率，可以使用下面一些高级优化算法可以更快地求偏导数。

1. 梯度下降(Gradient descent)
2. 共轭梯度(Conjugate gradient)
3. BFGS
4. L-BFGS

以上三种算法的详细介绍已经超出了本博客的内容，不详解。但这三种算法有共同的特点：

优点：

不需要自己手动选择学习速率，可智能选择合适的学习速率

比梯度下降法收敛的更快

缺点

比梯度下降法更复杂。

通常，我们不需要编写这些算法的代码，除非你是数值计算专家。我们一般是调用别人的软件库。Octave中就有这样的库，我们直接调用即可。需要注意的一点，如果你是使用其他高级语言如C++、Java，你可能需要多是几个不同的库，才能找到合适的算法。因为同一算法不同人编写的效率是不一样的，而这些算法的效率在数据量很大的情况下表现得差异特别明显。

3.2.4 示例：实现线性逻辑回归

参数：

代价函数：

代价函数偏导数：

样本数据data1.txt

本次算法的背景是，假如你是一个大学的管理者，你需要根据学生之前的成绩（两门科目）来预测该学生是否能进入该大学。

根据题意，我们不难分辨出这是一种二分类的逻辑回归，输入x有两种（科目1与科目2），输出有两种【能进入本大学（y=1）与不能进入本大学(y=0)】。输入测试样例以已经本文最前面贴出分别有两组数据。

34.62365962451697,78.0246928153624,0

30.28671076822607,43.89499752400101,0

35.84740876993872,72.90219802708364,0

60.18259938620976,86.30855209546826,1

79.0327360507101,75.3443764369103,1

45.08327747668339,56.3163717815305,0

61.10666453684766,96.51142588489624,1

75.02474556738889,46.55401354116538,1

76.09878670226257,87.42056971926803,1

84.43281996120035,43.53339331072109,1

95.86155507093572,38.22527805795094,0

75.01365838958247,30.60326323428011,0

82.30705337399482,76.48196330235604,1

69.36458875970939,97.71869196188608,1

39.53833914367223,76.03681085115882,0

53.9710521485623,89.20735013750205,1

69.07014406283025,52.74046973016765,1

67.94685547711617,46.67857410673128,0

70.66150955499435,92.92713789364831,1

76.97878372747498,47.57596364975532,1

67.37202754570876,42.83843832029179,0

89.67677575072079,65.79936592745237,1

50.534788289883,48.85581152764205,0

34.21206097786789,44.20952859866288,0

77.9240914545704,68.9723599933059,1

62.27101367004632,69.95445795447587,1

80.1901807509566,44.82162893218353,1

93.114388797442,38.80067033713209,0

61.83020602312595,50.25610789244621,0

38.78580379679423,64.99568095539578,0

61.379289447425,72.80788731317097,1

85.40451939411645,57.05198397627122,1

52.10797973193984,63.12762376881715,0

52.04540476831827,69.43286012045222,1

40.23689373545111,71.16774802184875,0

54.63510555424817,52.21388588061123,0

33.91550010906887,98.86943574220611,0

64.17698887494485,80.90806058670817,1

74.78925295941542,41.57341522824434,0

34.1836400264419,75.2377203360134,0

83.90239366249155,56.30804621605327,1

51.54772026906181,46.85629026349976,0

94.44336776917852,65.56892160559052,1

82.36875375713919,40.61825515970618,0

51.04775177128865,45.82270145776001,0

62.22267576120188,52.06099194836679,0

77.19303492601364,70.45820000180959,1

97.77159928000232,86.7278223300282,1

62.07306379667647,96.76882412413983,1

91.56497449807442,88.69629254546599,1

79.94481794066932,74.16311935043758,1

99.2725269292572,60.99903099844988,1

90.54671411399852,43.39060180650027,1

34.52451385320009,60.39634245837173,0

50.2864961189907,49.80453881323059,0

49.58667721632031,59.80895099453265,0

97.64563396007767,68.86157272420604,1

32.57720016809309,95.59854761387875,0

74.24869136721598,69.82457122657193,1

71.79646205863379,78.45356224515052,1

75.3956114656803,85.75993667331619,1

35.28611281526193,47.02051394723416,0

56.25381749711624,39.26147251058019,0

30.05882244669796,49.59297386723685,0

44.66826172480893,66.45008614558913,0

66.56089447242954,41.09209807936973,0

40.45755098375164,97.53518548909936,1

49.07256321908844,51.88321182073966,0

80.27957401466998,92.11606081344084,1

66.74671856944039,60.99139402740988,1

32.72283304060323,43.30717306430063,0

64.0393204150601,78.03168802018232,1

72.34649422579923,96.22759296761404,1

60.45788573918959,73.09499809758037,1

58.84095621726802,75.85844831279042,1

99.82785779692128,72.36925193383885,1

47.26426910848174,88.47586499559782,1

50.45815980285988,75.80985952982456,1

60.45555629271532,42.50840943572217,0

82.22666157785568,42.71987853716458,0

88.9138964166533,69.80378889835472,1

94.83450672430196,45.69430680250754,1

67.31925746917527,66.58935317747915,1

57.23870631569862,59.51428198012956,1

80.36675600171273,90.96014789746954,1

68.46852178591112,85.59430710452014,1

42.0754545384731,78.84478600148043,0

75.47770200533905,90.42453899753964,1

78.63542434898018,96.64742716885644,1

52.34800398794107,60.76950525602592,0

94.09433112516793,77.15910509073893,1

90.44855097096364,87.50879176484702,1

55.48216114069585,35.57070347228866,0

74.49269241843041,84.84513684930135,1

89.84580670720979,45.35828361091658,1

83.48916274498238,48.38028579728175,1

42.2617008099817,87.10385094025457,1

99.31500880510394,68.77540947206617,1

55.34001756003703,64.9319380069486,1

74.77589300092767,89.52981289513276,1

 Python代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import math
from collections import OrderedDict

#用于导入数据的函数
def inputData():
    #从txt文件中导入数据，注意最好标明数据的类型
    data = pd.read_csv('D:/dataAnalysis/MachineLearning/data1.txt'
                       ,names = ['Exam1 Score','Exam2 Score','Label']
                       ,dtype={0:float,1:float,2:int})
    #插入一列全为1的列
    data.insert(0,"one",[1 for i in range(0,data.shape[0])])
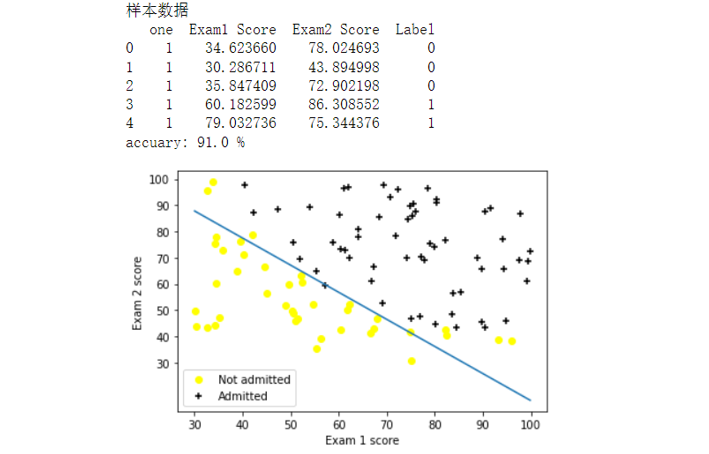
    print('样本数据')
    print(data.head())
    #分别取出X和y
    X=data.iloc[:,0:3].values
    y=data.iloc[:,3].values
    y=y.reshape(y.shape[0],1)
    return X,y

#用于最开始进行数据可视化的函数
def showData(X,y):
    #分开考虑真实值y是1和0的行，分别绘制散点，并注意使用不同的label和marker
    for i in range(0,X.shape[0]):
        if(y[i,0]==1):
            plt.scatter(X[i,1],X[i,2],marker='+',c='black',label='Admitted')
        elif(y[i,0]==0):
            plt.scatter(X[i,1],X[i,2],marker='o',c='yellow',label='Not admitted')
    #设置坐标轴和图例
    plt.xticks(np.arange(30,110,10))
    plt.yticks(np.arange(30,110,10))
    plt.xlabel('Exam 1 score')
    plt.ylabel('Exam 2 score')
    #因为上面绘制的散点不做处理的话，会有很多重复标签
    #因此这里导入一个集合类消除重复的标签
    handles, labels = plt.gca().get_legend_handles_labels()     #获得标签
    by_label = OrderedDict(zip(labels, handles))            #通过集合来删除重复的标签
    plt.legend(by_label.values(), by_label.keys())          #显示图例
    plt.show()

#定义sigmoid函数
def sigmoid(z):
    return 1/(1+np.exp(-z))

#计算代价值的函数
def showCostsJ(X,y,theta,m):
    #根据吴恩达老师上课讲的公式进行书写
    #注意式子中加了1e-6次方是为了扩大精度，防止出现除0的警告
    costsJ = ((y*np.log(sigmoid(X@theta)+ 1e-6))+((1-y)*np.log(1-sigmoid(X@theta)+ 1e-6))).sum()/(-m)
    return costsJ

#用于进行梯度下降的函数
def gradientDescent(X,y,theta,m,alpha,iterations):
    for i in range(0,iterations):       #进行迭代
        # 进行向量化的计算。
        #注意下面第二行使用X.T@ys可以替代掉之前的同步更新方式，写起来更简洁
        ys=sigmoid(X@theta)-y
        theta=theta-alpha*(X.T@ys)/m

        #以下完全代码，可以代替上面两行的代码
        # temp0=theta[0][0]-alpha*(ys*(X[:,0].reshape(X.shape[0],1))).sum()  #注意这里一定要将X[:,1]reshape成向量
        # temp1=theta[1][0]-alpha*(ys*(X[:,1].reshape(X.shape[0],1))).sum()
        # temp2=theta[2][0]-alpha*(ys*(X[:,2].reshape(X.shape[0],1))).sum()
        # theta[0][0]=temp0          #进行同步更新θ0和θ1和θ2
        # theta[1][0]=temp1
        # theta[2][0]=temp2
        
    return theta

#对决策边界进行可视化的函数
def evaluateLogisticRegression(X,y,theta):

    #这里和上面进行数据可视化的函数步骤是一样的，就不重复阐述了
    for i in range(0,X.shape[0]):
        if(y[i,0]==1):
            plt.scatter(X[i,1],X[i,2],marker='+',c='black',label='Admitted')
        elif(y[i,0]==0):
            plt.scatter(X[i,1],X[i,2],marker='o',c='yellow',label='Not admitted')
    plt.xticks(np.arange(30,110,10))
    plt.yticks(np.arange(30,110,10))
    plt.xlabel('Exam 1 score')
    plt.ylabel('Exam 2 score')
    handles, labels = plt.gca().get_legend_handles_labels()
    by_label = OrderedDict(zip(labels, handles))
    plt.legend(by_label.values(), by_label.keys())

    minX=np.min(X[:,1])         #取得x1中的最小值
    maxX=np.max(X[:,1])         #取得x1中的最大值
    xx=np.linspace(minX,maxX,100)   #创建等间距的数100个
    yy=(theta[0][0]+theta[1][0]*xx)/(-theta[2][0])      #绘制决策边界
    plt.plot(xx,yy)
    plt.show()

#利用训练集数据判断准确率的函数
def judge(X,y,theta):
    ys=sigmoid(X@theta)         #根据假设函数计算预测值ys
    yanswer=y-ys                #使用真实值y-预测值ys
    yanswer=np.abs(yanswer)     #对yanswer取绝对值
    print('accuary:',(yanswer<0.5).sum()/y.shape[0]*100,'%')   #计算准确率并打印结果

X,y = inputData()           #输入数据   
theta=np.zeros((3,1))       #初始化theta数组
alpha=0.004                 #设定alpha值
iterations=200000           #设定迭代次数
theta=gradientDescent(X,y,theta,X.shape[0],alpha,iterations)        #进行梯度下降
judge(X,y,theta)            #计算准确率
evaluateLogisticRegression(X,y,theta)       #决策边界可视化

 

 

3.3.5 示例：实现非线性逻辑回归(Logistic Regression)

样本数据data2.txt

0.051267,0.69956,1

-0.092742,0.68494,1

-0.21371,0.69225,1

-0.375,0.50219,1

-0.51325,0.46564,1

-0.52477,0.2098,1

-0.39804,0.034357,1

-0.30588,-0.19225,1

0.016705,-0.40424,1

0.13191,-0.51389,1

0.38537,-0.56506,1

0.52938,-0.5212,1

0.63882,-0.24342,1

0.73675,-0.18494,1

0.54666,0.48757,1

0.322,0.5826,1

0.16647,0.53874,1

-0.046659,0.81652,1

-0.17339,0.69956,1

-0.47869,0.63377,1

-0.60541,0.59722,1

-0.62846,0.33406,1

-0.59389,0.005117,1

-0.42108,-0.27266,1

-0.11578,-0.39693,1

0.20104,-0.60161,1

0.46601,-0.53582,1

0.67339,-0.53582,1

-0.13882,0.54605,1

-0.29435,0.77997,1

-0.26555,0.96272,1

-0.16187,0.8019,1

-0.17339,0.64839,1

-0.28283,0.47295,1

-0.36348,0.31213,1

-0.30012,0.027047,1

-0.23675,-0.21418,1

-0.06394,-0.18494,1

0.062788,-0.16301,1

0.22984,-0.41155,1

0.2932,-0.2288,1

0.48329,-0.18494,1

0.64459,-0.14108,1

0.46025,0.012427,1

0.6273,0.15863,1

0.57546,0.26827,1

0.72523,0.44371,1

0.22408,0.52412,1

0.44297,0.67032,1

0.322,0.69225,1

0.13767,0.57529,1

-0.0063364,0.39985,1

-0.092742,0.55336,1

-0.20795,0.35599,1

-0.20795,0.17325,1

-0.43836,0.21711,1

-0.21947,-0.016813,1

-0.13882,-0.27266,1

0.18376,0.93348,0

0.22408,0.77997,0

0.29896,0.61915,0

0.50634,0.75804,0

0.61578,0.7288,0

0.60426,0.59722,0

0.76555,0.50219,0

0.92684,0.3633,0

0.82316,0.27558,0

0.96141,0.085526,0

0.93836,0.012427,0

0.86348,-0.082602,0

0.89804,-0.20687,0

0.85196,-0.36769,0

0.82892,-0.5212,0

0.79435,-0.55775,0

0.59274,-0.7405,0

0.51786,-0.5943,0

0.46601,-0.41886,0

0.35081,-0.57968,0

0.28744,-0.76974,0

0.085829,-0.75512,0

0.14919,-0.57968,0

-0.13306,-0.4481,0

-0.40956,-0.41155,0

-0.39228,-0.25804,0

-0.74366,-0.25804,0

-0.69758,0.041667,0

-0.75518,0.2902,0

-0.69758,0.68494,0

-0.4038,0.70687,0

-0.38076,0.91886,0

-0.50749,0.90424,0

-0.54781,0.70687,0

0.10311,0.77997,0

0.057028,0.91886,0

-0.10426,0.99196,0

-0.081221,1.1089,0

0.28744,1.087,0

0.39689,0.82383,0

0.63882,0.88962,0

0.82316,0.66301,0

0.67339,0.64108,0

1.0709,0.10015,0

-0.046659,-0.57968,0

-0.23675,-0.63816,0

-0.15035,-0.36769,0

-0.49021,-0.3019,0

-0.46717,-0.13377,0

-0.28859,-0.060673,0

-0.61118,-0.067982,0

-0.66302,-0.21418,0

-0.59965,-0.41886,0

-0.72638,-0.082602,0

-0.83007,0.31213,0

-0.72062,0.53874,0

-0.59389,0.49488,0

-0.48445,0.99927,0

-0.0063364,0.99927,0

0.63265,-0.030612,0

Python代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict

#用于导入数据的函数
def inputData():
    #从txt文件中导入数据，注意最好标明数据的类型
    data = pd.read_csv('D:/dataAnalysis/MachineLearning/ex2data2.txt'
                       ,names = ['Microchip test 1','Microchip test 2','Label']
                       ,dtype={0:float,1:float,2:int})
    #插入一列全为1的列
    data.insert(0,"ones",np.ones((data.shape[0],1)))
    print(data.head())
    #分别取出X和y
    X=data.iloc[:,0:3]
    X=X.values
    y=data.iloc[:,3]
    y=(y.values).reshape(y.shape[0],1)
    return X,y

#用于最开始进行数据可视化的函数
def showData(X,y):
    #分开考虑真实值y是1和0的行，分别绘制散点，并注意使用不同的label和marker
    for i in range(0,X.shape[0]):
        if(y[i][0]==1):
            plt.scatter(X[i][1],X[i][2],marker="+",c='b',label='y=1')
        else:
            plt.scatter(X[i][1],X[i][2],marker='o',c='y',label='y=0')
    #设置坐标轴和图例
    plt.xticks(np.arange(-1,1.5,0.5))
    plt.yticks(np.arange(-0.8,1.2,0.2))
    plt.xlabel('Microchip Test 1')
    plt.ylabel('Microchip Test 2')
    #因为上面绘制的散点不做处理的话，会有很多重复标签
    #因此这里导入一个集合类消除重复的标签
    handles, labels = plt.gca().get_legend_handles_labels()     #获得标签
    by_label = OrderedDict(zip(labels, handles))                #通过集合来删除重复的标签
    plt.legend(by_label.values(), by_label.keys())              #显示图例
    plt.show()

#定义sigmoid函数
def sigmoid(z):
    return 1/(1+np.exp(-z))

#计算代价值的函数
def computeCostsJ(X,y,theta,lamda,m):
    #根据吴恩达老师上课讲的公式进行书写
    hx=sigmoid(X@theta)
    costsJ=-(np.sum(y*np.log(hx)+(1-y)*np.log(1-hx)))/m+lamda*np.sum(np.power(theta,2))/(2*m)
    return costsJ

#进行特征映射
def featureMapping(x1,x2,level):
    answer = {}         #定义一个字典
    for i in range(1,level+1):      #外层循环，映射的阶数
        for j  in range(0,i+1):     #内存循环，x1的次数
            answer['F{}{}'.format(i-j,j)]=np.power(x1,i-j)*np.power(x2,j)    #形成字典中的key-value   
    answer = pd.DataFrame(answer)       #转换为一个dataframe
    answer.insert(0,"ones",np.ones((answer.shape[0],1)))        #插入第一列全1
    return answer.values

#进行梯度下降的函数
def gradientDescent(X,y,theta,alpha,iterations,m,lamda):
    for i in range(0,iterations+1):
        hx=sigmoid(X@theta)
        temp0=theta[0][0]-alpha*np.sum(hx-y)/m          #因为x0是不需要进行正则化的，因此需要单独计算
        theta=theta-alpha*(X.T@(hx-y)+lamda*theta)/m    #根据公式进行同步更新theta
        theta[0][0]=temp0                           #单独修改theta0
    return theta

#利用训练集数据判断准确率的函数
def judge(X,y,theta):
    ys=sigmoid(X@theta)         #根据假设函数计算预测值ys
    yanswer=y-ys                #使用真实值y-预测值ys
    yanswer=np.abs(yanswer)     #对yanswer取绝对值
    print('accuary',(yanswer<0.5).sum()/y.shape[0]*100,'%')    #计算准确率并打印结果

#对决策边界进行可视化的函数
def evaluateLogisticRegression(X,y,theta):
    #这里和上面进行数据可视化的函数步骤是一样的，就不重复阐述了
    for i in range(0,X.shape[0]):
        if(y[i][0]==1):
            plt.scatter(X[i][1],X[i][2],marker="+",c='b',label='y=1')
        else:
            plt.scatter(X[i][1],X[i][2],marker='o',c='y',label='y=0')
    plt.xticks(np.arange(-1,1.5,0.5))
    plt.yticks(np.arange(-0.8,1.2,0.2))
    plt.xlabel('Microchip Test 1')
    plt.ylabel('Microchip Test 2')
    handles, labels = plt.gca().get_legend_handles_labels()
    by_label = OrderedDict(zip(labels, handles))
    plt.legend(by_label.values(), by_label.keys())
    
    #通过绘制等高线图来绘制决策边界
    x=np.linspace(-1,1.5,250)       #创建一个从-1到1.5的等间距的数
    xx,yy = np.meshgrid(x,x)        #形成一个250*250的网格，xx和yy分别对应x值和y值
    #利用ravel()函数将xx和yy变成一个向量，也就是62500*1的向量
    answerMapping=featureMapping(xx.ravel(),yy.ravel(),6)   #进行特征映射
    answer=answerMapping@theta      #代入映射后的数据进行计算预测值
    answer=answer.reshape(xx.shape) #将answer换成一样格式
    plt.contour(xx,yy,answer,0)     #绘制等高线图，0代表绘制第一条等高线
    plt.show()

X,y = inputData()       #导入数据
theta=np.zeros((28,1))      #初始化theta数组
iterations=200000       #定义迭代次数
alpha=0.001             #定义alpha值
lamda=1                 #定义lamda
print(f'lamda = {lamda}')
mappingX = featureMapping(X[:,1],X[:,2],6)      #进行特征映射
theta=gradientDescent(mappingX,y,theta,alpha,iterations,X.shape[0],lamda)   #进行正则化的梯度下降
judge(mappingX,y,theta)         #计算预测的准确率
evaluateLogisticRegression(X,y,theta)       #绘制决策边界
lamda=100               #定义lamda
print(f'lamda = {lamda}')
mappingX = featureMapping(X[:,1],X[:,2],6)      #进行特征映射
theta=gradientDescent(mappingX,y,theta,alpha,iterations,X.shape[0],lamda)   #进行正则化的梯度下降
judge(mappingX,y,theta)         #计算预测的准确率
evaluateLogisticRegression(X,y,theta)       #绘制决策边界