开学第一课

​

一、加入qq群

(一)班级qq群：703173397

（二）入群要求

• 修改名片，使用实名
  

二，加入学习通班级群

（一）学习通班级群

• 2023数据一班邀请码：84554639
  

（二）手势签到

三使用思维导图工具

（一）安装XMind

• 安装完后，桌面会有快捷方式图标
• 

（二）创建思维导图做自我介绍

• 自我介绍（罗明雪-2024）
  

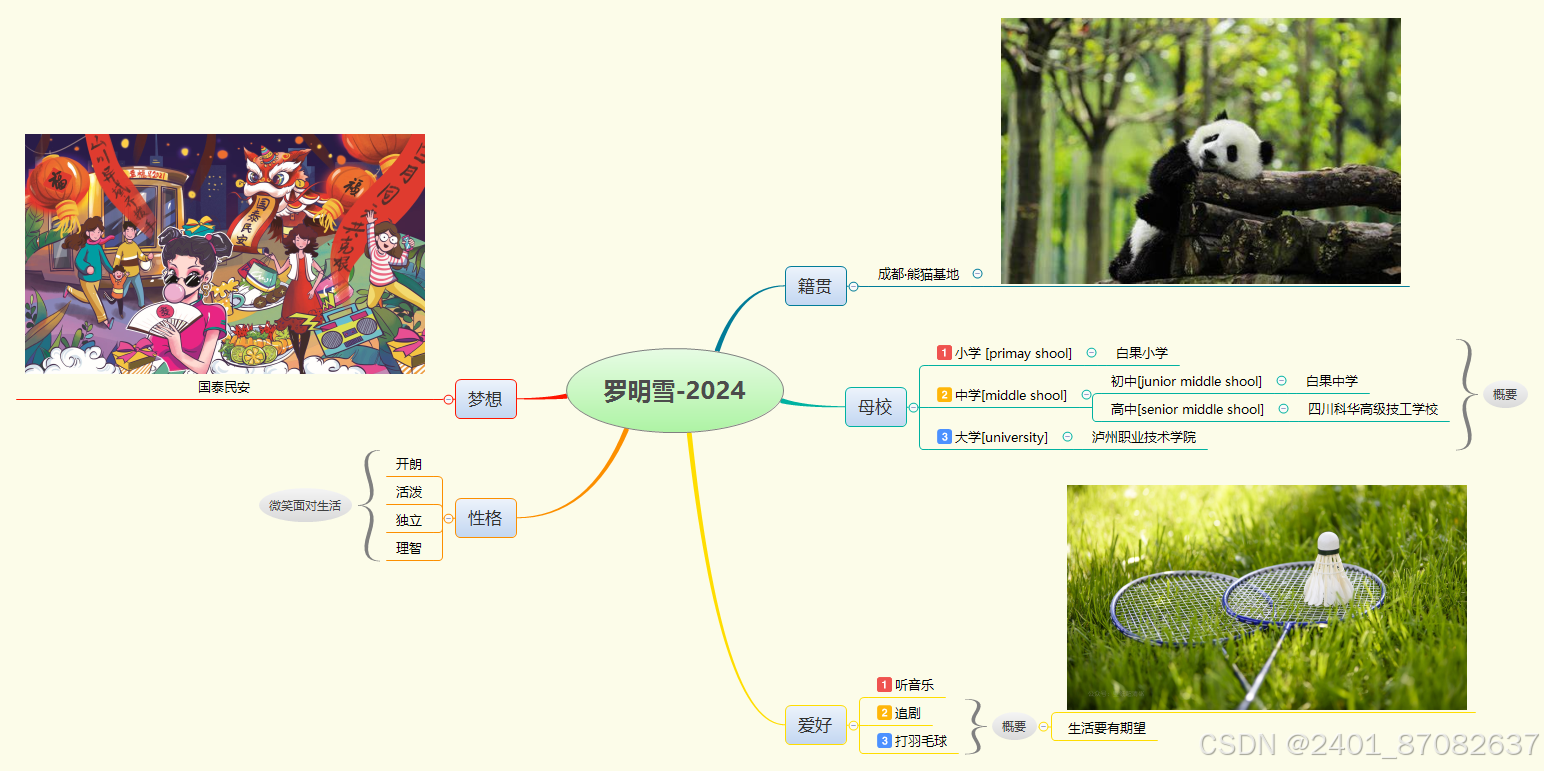
（三）操作要点小结

-选择模板、选择风格

• 添加字节

  • 添加字节兄弟点：按tap键
  • 添加 兄弟节点，按enter键

• 删除节点：选中节点，按del键

• 给节点添加图标（任务优先级）
  

• 生成概要（summary）
  

• 保存思维导图

• 导出成ping图片

四，使用大语言模型

• 有很多大语言模型，比如ChatGPT、通义千问、文心一言、豆包
• 我们使用通义千问（https://tongyi.aliyun.com/qianwen/）
  
• 注册登录
  
• 将思维导图的自我介绍写成一篇具有某种风格的自我介绍文章
  -
• 单击【发送】按钮，生成满足用户要求的文字
  

五，创建CSDN博客

（一）选择MarkDown编辑器

• 在内容管理的博客设置里，选择默认编辑器：MarkDown编辑器

• 注意，千万不要忘了单击【保存】按钮，这样才能让设置生效

（二）MarkDown基本语法

1、自动生成文章目录

• 在文章最前面添加注解：@[toc]\

2、各个级别标题

• # ： 一级标题
• ## ：二级标题
• ###： 三级标题
• 注意：#打完之后必须空一格

3、让内容变红

• 用一对反单引号：``

4、制作表格

• 2023级数据1班

学号	姓名	性别	年龄	班级	电话
232064009	罗明雪	女	19	2023数据1班	19980826353
232064010	侯显柯	男	20	2023数据1班	18683173170
232062009	罗明琴	女	19	2023软件3班	18782456704

5、数学公式

• 勾股定理：$a^2+b^2=c^2$
• 一元二次方程:$a{x}^2+bx+c=0$
• 求根公式:
  • $x_1=\frac{-b+\sqrt{b^2-4ac}}{2a}$
  • $x_2=\frac{-b+\sqrt{b^2-4ac}}{2a}$
  • $x_3=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$
  • $x_3=\frac{-b\mp \sqrt{b^2-4ac}}{2a}$
• 不等式：
• $x+4>6$gt:greater than
• $3+2x<6$lt:less than
• $x+4\ge 6$ge:greater than or equal to
• $3+2x\le 6$le:less than or equal to

6、不定积分

（1）公式

• $\int f(x)dx=F(x)+C,F^{\prime }(x)=f(x)$

（2）示例

• 求$f(x)=x^2-3x+2$的不定积分
• $\int f(x)dx=\int (x^2-3x+2)dx=\left(\frac{x^3}{3}-\frac{3x^2}{2}+2x\right)+C$

（3）利用Python计算不定积分

• 需要导入sympy和scipy两个库
• 

7、定积分

（1）公式

• 牛顿 - 莱布尼茨公式：${\int }_a^{b}f(x)dx=F(x)|\genfrac{}{}{0ex}{}{b}{a}=F(b)-F(a)$

（2）示例

• ${\int }_1^{2}f(x)dx={\int }_1^2(x^2-3x+2)dx=\left(\frac{x^3}{3}-\frac{3x^2}{2}+2x\right)|\genfrac{}{}{0ex}{}{2}{1}=\left(\frac{8}{3}-6+4\right)-\left(\frac{1}{3}-\frac{3}{2}+2\right)=\frac{2}{3}-\frac{5}{6}=-\frac{1}{6}$

（3）利用Python计算定积分

• 需要导入sympy和scipy两个库