八大排序之希尔排序

希尔排序是直接插入排序的优化算法，本篇文章将带你详细了解希尔排序其背后的原理。

---

（一）希尔排序的前身

希尔排序是直接插入排序的优化版。前人在分析直接插入排序的时间复杂度中发现，直接插入排序在数据靠近有序的时候效率特别高，可以靠近O(N)，反之，如果数据完全乱序，比如我们要排升序，但要排序的数据是降序的，这个时候算法的时间复杂度就会退化到O(N2)。这是为什么呢？因为直接插入排序那种情况下，每一插入一个数据几乎都要从数据组的后端排查到前端，即遍历了整个数据组，插入数据的跨越值太大了，算法就会退化。所以，为了防止这种情况的发生，前人们总结了经验，发明了希尔排序。

（二）希尔排序的具体原理

直接插入排序退化的原因是乱序程度高的时候每插入数据都几乎要遍历数组。有什么办法可以防止这种情况发生呢?前人想到我们可以先把数据分组，把每相隔gap个位置的元素划分成一组，把每组的元素先直接插入排序一下，这样我们在排全部数据的时候，数据就会几乎有序了。希尔排序通过分组，让元素可以远距离移动，提前将 “离正确位置较远” 的元素快速调整到更接近目标的位置，减少后续插入排序的工作量。我们可以设gap=n（数组元素），先把间隔为n的元素组排序。然后做成一个循环。每循环一次，gap就自减，直到减到1为止。发现没有？当gap=1时，该排序就是正儿八经的直接插入排序，但这个时候数组已经几乎有序了，所有最后一次排序的效率很高，可以达到O（N）。

（三）希尔排序的动图及排序中的过程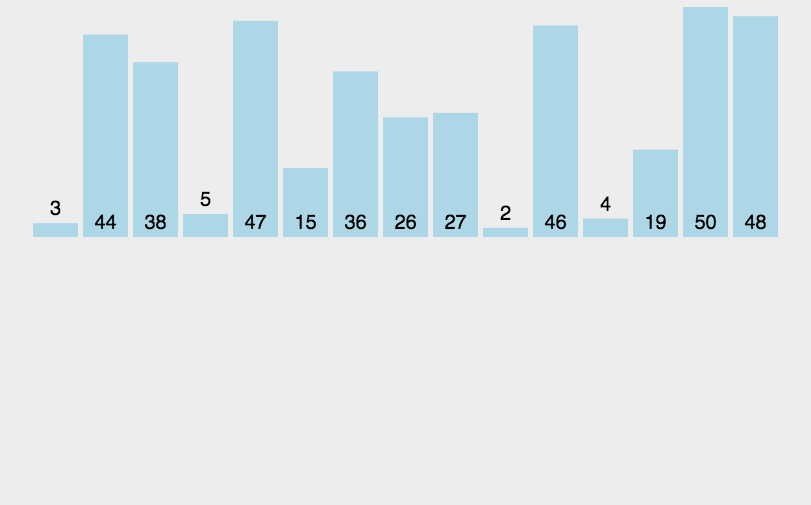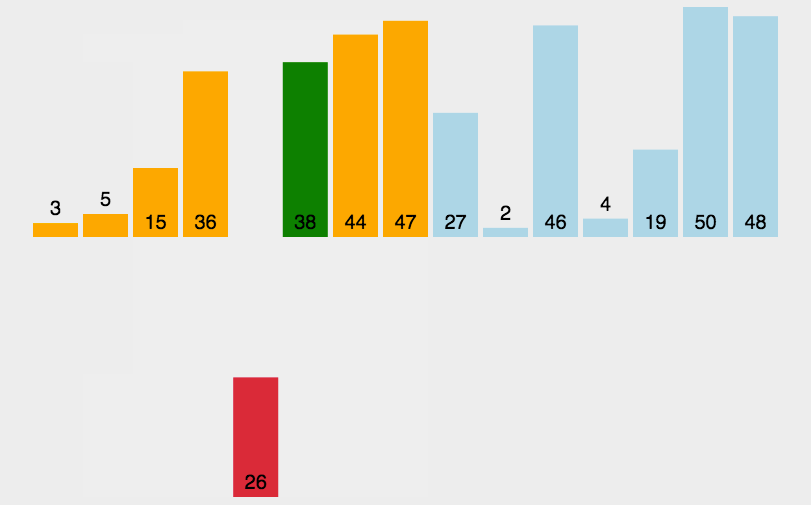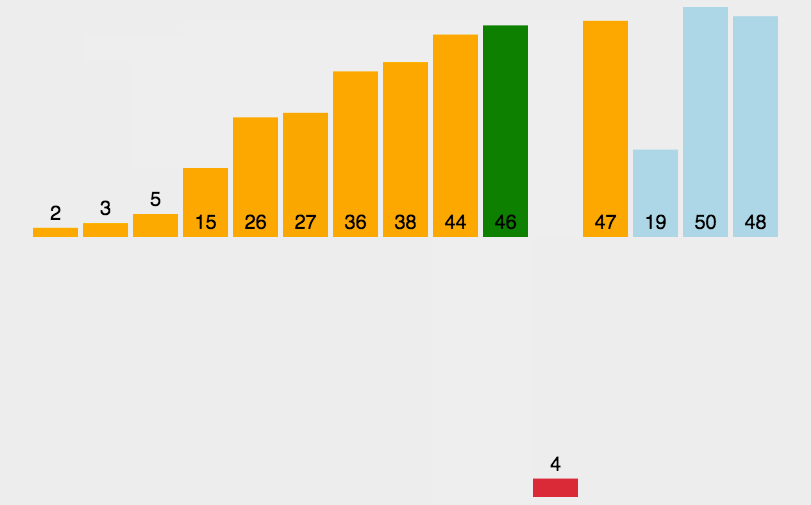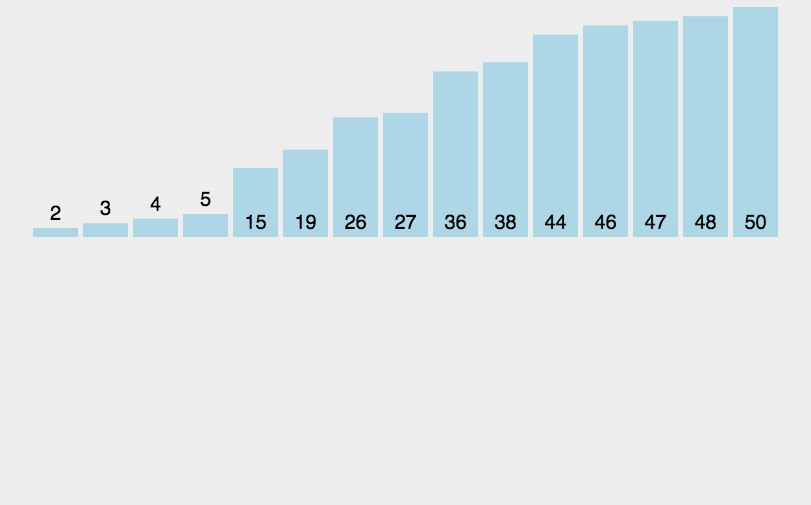

（五）时间复杂度和空间复杂度分析

• 最坏情况
• 希尔排序最坏情况下的时间复杂度为 O(n2) 。当增量序列选择不当时，例如采用希尔最初提出的增量序列 ht​=⌊n/2⌋,ht−1​=⌊ht​/2⌋,⋯,h1​=1 时，最坏情况下就会达到 O(n2) 。在最坏情况下，每次分组插入排序都需要进行大量的元素移动操作，导致时间复杂度较高。
• 最好情况
• 在最好情况下，即数组已经是有序的，希尔排序的时间复杂度为 O(n) 。因为在数组有序的情况下，每个子序列在进行插入排序时，元素几乎不需要移动，所以总的比较次数和移动次数接近线性。
• 平均情况
• 希尔排序平均情况下的时间复杂度难以精确分析，它取决于增量序列的具体选择。经过大量实验和研究表明，一些较好的增量序列可以使希尔排序的平均时间复杂度接近 O(n1.3) 。例如，Knuth 提出的增量序列 h=3×h+1（初始 h=1 ），在平均情况下能有较好的性能表现。
• 空间复杂度
• 空间复杂度为O（1），是原地排序算法。

 （六）原代码

void Shell(int* arr, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = arr[end + gap];
			while (end >= 0)
			{
				if (arr[end] > tmp)
				{
					arr[end + gap] = arr[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			arr[end + gap] = tmp;
		}
	}
}