牛顿迭代法求方程的根

求f(x)=2*x*x*x-4*x*x+3*x-6=0 ,在1.5附近的根

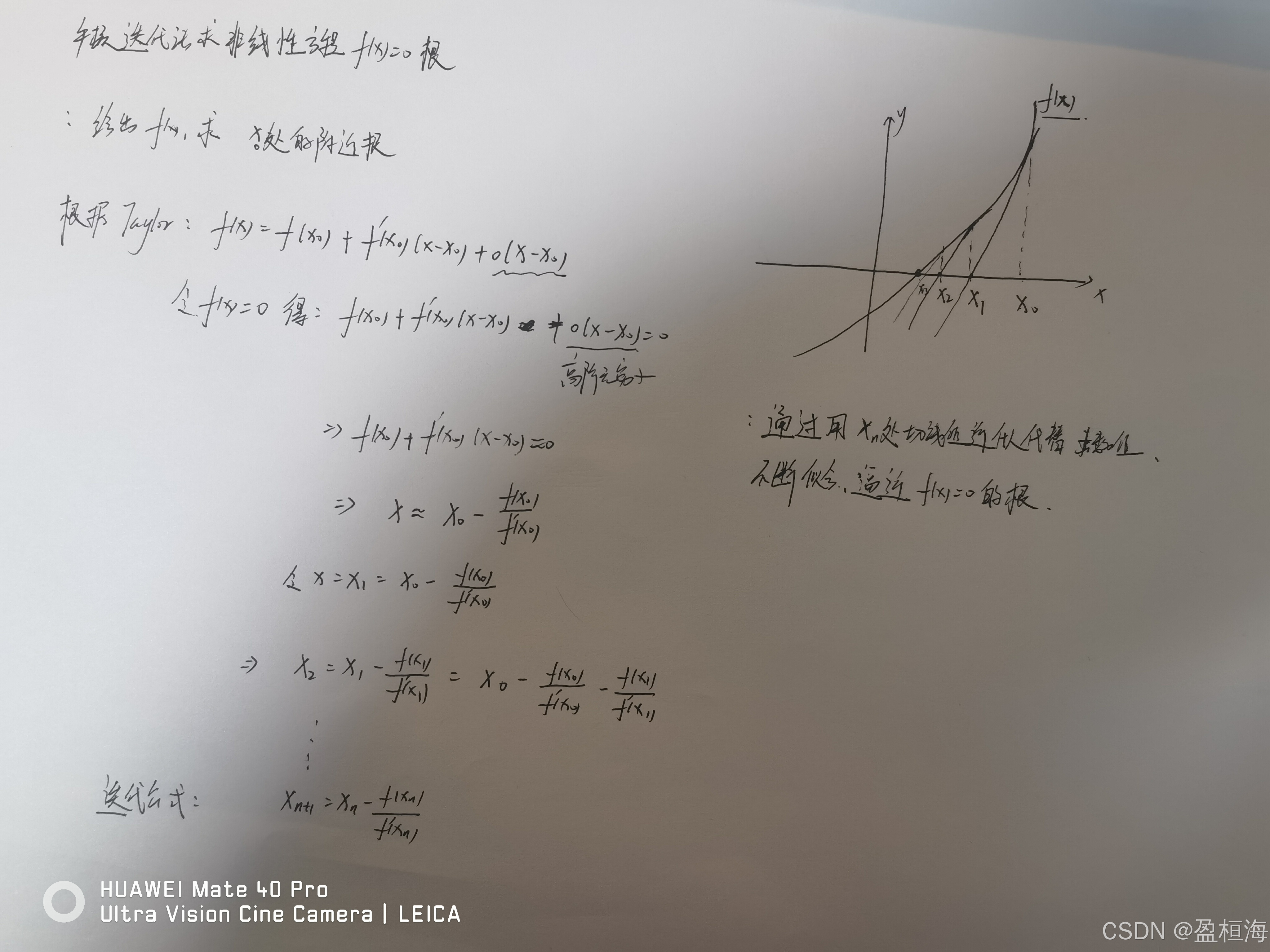
思想：利用一阶Taylor 即切线方程的根来不断迭代，逼近方程的根。

迭代公式 xn+1=xn - f(xn)/f'(xn) 

//2*x*x*x-4*x*x+3*x-6=0 在x=1.5附近的根  精度1e-8
#include<stdio.h>
#include<math.h>
double fun(double x){
	return 2*pow(x,3)-4*pow(x,2)+3*x-6;//函数值
}
double fun1(double x){
	return 6*pow(x,2)+8*x+3;//切线值
}
double Newton(){
	double x1=1.5,x2=x1-fun(x1)/fun1(x1);
	while(fabs(x2-x1)>1e-8){
		x1=x2;
		x2=x1-fun(x1)/fun1(x1);//迭代公式
	}
	return x2;
}
int main(){
	printf("%f",Newton());
	return 0;
}