“函数总结”只需你轻轻点开

   “凌晨三点半，海棠花未眠”，如果你未寝，不如与我一起相步于函数的世界吧！ 

目录

常见的库函数：

自定义函数：

函数定义：

函数调用：

传值调用：

传址调用：

链式访问：

函数的原型声明：

const类型修饰符：

作用域：

存储期：

自动存储期：

静态存储期：

递归函数：

阶乘：

斐波拉契数列：

如何解决递归的问题：

结语：

---

常见的库函数：

在库函数中由我们经常遇到的main,printf,scanf函数，还有一些我们可能用到的strcpy(string.h,以“\0"结束的字符串的复制),pow,sqrt(math.h,前面用于求次方,后面用于求平方根),assert(assert.h,检查程序某个条件是否为真),strlen(string.h,用于计算字符串的长度)。

以上就是我们可能接触较多的，还有很多库函数我便不再一一列举(可以通过网站查询哦!)，但是库函数的种类是有限的，并不能解决我们方方面面的问题，所以我们要自定义函数，自定义函数需要满足什么条件，接下来我们带着这个疑问来了解它！

自定义函数：

函数定义：

它(函数定义)包括函数头,返回类型,函数名,形参声明，比如自定义Add函数：

返回类型：double,int,float...或者是无返回类型void。

函数名称：虽然不受限制，但最好根据函数功能对应英文来写，这样方便理解!

形参声明：顾名思义就是形式参数的声明(也可以不含形参void)。

函数调用：

传值调用：

Add(实参)，将实参的值赋予给形参，return返回一个值由定义的sum变量来接收，且调用函数是“传值”是“单向传递”(值传递)，由实参传给形参，所以形参值的改变不会反向影响实参的值！传参时，实参不至一个时，可以用“,”将其隔开。举个例子(形参不会改变实参)

传址调用：

把函数外部创建变量的内存地址传给函数参数的调用方式，可以让函数和函数外部建立直接的联系。

这样通过地址就能将数值修改，要用指针去修改，传递则需要&；

我们需要记住一个知识点，传递数组时传递的是数组首元素的地址！

函数可以嵌套调用，但函数不能嵌套定义！

链式访问：

把一个函数的返回值作为另外一个函数的参数

函数的原型声明：

函数的原型声明包括函数返回类型,形参类型和个数(该声明以“  ; ”结尾)，它并没有定义函数的实体，这是与函数定义的区别！若函数在main函数之前，一般用不到函数的原型声明。

const类型修饰符：

若我们想要将数组赋值，但我们不想改变原来的数组元素的值，这时const能使只是引用所接收的值，但不改写

作用域：

可能大家会觉得函数与作用域有啥关联？比如当我们在主函数定义了a和b，在调用函数中我们会觉得我们定义了该变量，则return a+b,但却出现了错误说变量未定义，这时我们应该知道这是定义域在装神弄鬼，我们先聊块作用域——变量名称从声明变量开始到最后的大括号结束“ } ”；

图中Print,main就相当于两个“块作用域”。若定义全局变量，则能在整个文件作用域中使用

存储期：

自动存储期：

自动存储期是不被static(存储类说明符)而定义出的变量，执行到声明时创建出的对象，执行到程序的结尾，对象就会消失。除此，不显示地进行初始化，它将会初始化为不确定的值

静态存储期：

使用static定义的对象，它是在main函数之前被创建出来，到程序结束时消失。如果不显示地初始化，该对象会被自动初始化为0。（全局变量都是静态存储变量）

为什么a++之后a仍为0？a为“块作用域+自动存储期”所以当a出了func函数将自动销毁，重新调用时a又被赋值为0了，而b,c分别为“块作用域+静态存储期”,“文件作用域+静态存储期”，故而它们的生命周期为整个程序，所以出了func也并未消失。

递归函数：

递归函数就是调用和该函数相同的函数，满足递归两个条件：

(一) 存在限制条件，满足限制条件时，便不再发生递归。

(二) 每次递归调用后越来越接近这个条件

阶乘：

n != n * (n-1) * (n-2)...* 1我们可能会先想到用循环：

那除了循环，我们还可以用什么方法呢？这时我们再分析一下阶乘，n! = n * (n-1)!，n-1的阶乘我们可以一直调用函数，而这种方法便叫作“递归”！又该怎么写(答案就在我们的分析)？

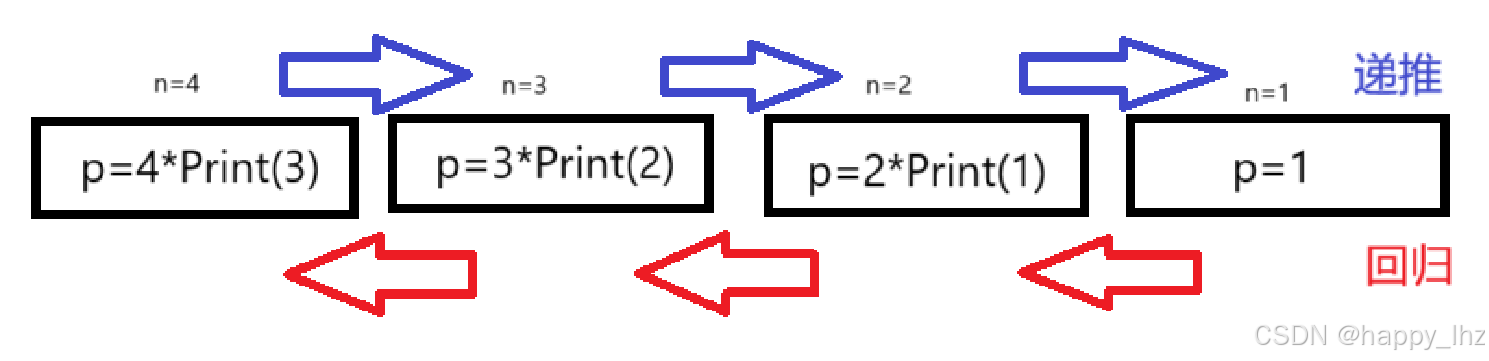
从这个例子，我们便能知道要想写好递归我们应该做好分析，递归写出的代码较为简洁，但如果输入数值较大，可能会很久才会打印或者栈溢出的现象，从而导致效率不高；“递归”虽好，但我们需谨慎使用哦！

斐波拉契数列：

我们先了解它：1 1 2 3 5 8.....我们发现除了前两项，后一项为前两项的和；这时如果我们求第n个斐波拉契数，则分析出n = (n-1)+(n-2)；通过我们的分析便能写出递归函数了，这里就留着给你们去练习吧！

思考：

就我个人而言，从上述例子我认为学好递归，需要分析能力，同时不要把递归看作做一个“新概念”，就是把它当作反复地去调用函数，这样我认为方便理解！

如何解决递归的问题：

(一) 将递归改为非递归

(二) 将局部变量改为静态变量(static)

结语：

这一篇博客终于补完了！我希望能够继续坚持带更多的作品与君共享，谢谢大家观看了！