一、图的概念
一、图的表示:
图G由俩个集合V和E组成,即为G=(V,E),其中V是顶点的有限非空集合,E是V中顶点偶对的有限集,这些顶点偶对称为边(或弧)。
二、图的分类:
(1)根据边有无方向:有向图和无向图
有向图: 图中所有的边都是有向边(弧),有向边的起点称为弧尾,有向边的终点称为弧头。

无向图:图中所有的边都是无向边。注意:一条无向边 相当于 俩条方向相反的有向边。

(2)根据边是否带权值:带权图和无权图
带权图:图中的边都附有一个权值(可为整数,实数,负数等)。注意:边的权值都相等的图 相当于 无权图。

无权图:图中的边不附有一个权值。

(3)根据图中是否带自边或重边:简单图和非简单图
简单图:图中不存在自边(自己到自己的边)和重边(重复的边)。
非简单图:图中存在自边或重边。如下图,B顶点存在自边,顶点A到顶点C存在重边。

(4)根据图中是否存在环(回路):带环图和无环图
带环图: 图中存在环(回路)。

无环图:图中不存在环(回路)。如下图,实际上不存在环,因为从顶点2出发都无法回到顶点2.

(5)完全图:
图中的每俩个顶点间都存在一条边。完全有向图:存在n*(n-1)条边;完全无向图:存在n*(n-1)/2条边。
(6)顶点数目固定,根据边的数目分为:稠密图和稀疏图
稠密图:当图接近于完全图或通常认为图中边数大于n*log(n) (n为顶点数)的图。
稀疏图:当图含较少的边或通常认为图中边数小于n*log(n) 的图。
三、图的概念:
(1)端点和邻接点:构成一条边的俩个顶点为端点,他们俩个互为邻接点。
(2)子图:
存在俩个图G=(V,E)和G'=(V',E'),若V'是V的子集,E'是E的子集,且E'是V'中的顶点偶对的有限集,则G'是G的子图。
(3)度:
无向图中:顶点的度就是一个顶点所连的边数。
有向图中:分为顶点的出度和入度:出度为以该顶点为弧尾的边的数目;入度为以该顶点为弧头的边的数目。顶点的度为出度+入度之和。
有向图还是无向图,图中所有的顶点的度之和一定为偶数。有n条边,度之和为2n。
(4)路径和路径长度:
路径:在图G中,从顶点i到顶点j的一条路径即为途中经过的顶点序列(i,......,j)。
路劲长度:在无权图中,路径长度为起点到终点所经过的边的数目;在带权图中,路径长度为起点到终点经过的边的权值之和。
(5)环/回路:
若一条路径从起点出发,经过若干点,最终回到起点,则这条路径称为环(回路)。若一条环中只存在起点和终点是相同的顶点,则这条环称为简单环或简单回路。
特殊的回路:
欧拉环路:经过图中的各个边一次仅且一次的环,其长度为图中的边的总数。
哈密尔顿环路:经过图中的所有顶点一次仅且一次的环,其长度为构成环的边的数目。

(6)连通、连通图、连通分量、生成树(均为无向图中存在):
连通:若顶点x与y之间存在可相互抵达的路径(无论是直接或间接),则称为连通。
连通图:图中任意俩个顶点都连通的图。
连通分量:即极大联通子图。对于连通图来说,只存在一个极大连通子图(连通分量)即它本身;对于非连通图来说,存在多个极大联通子图(即多个连通分量),每个连通分量都是一个连通图。
生成树:即极小连通子图。即在无向连通图中,选n-1条边使得图中的全部n个顶点连通。
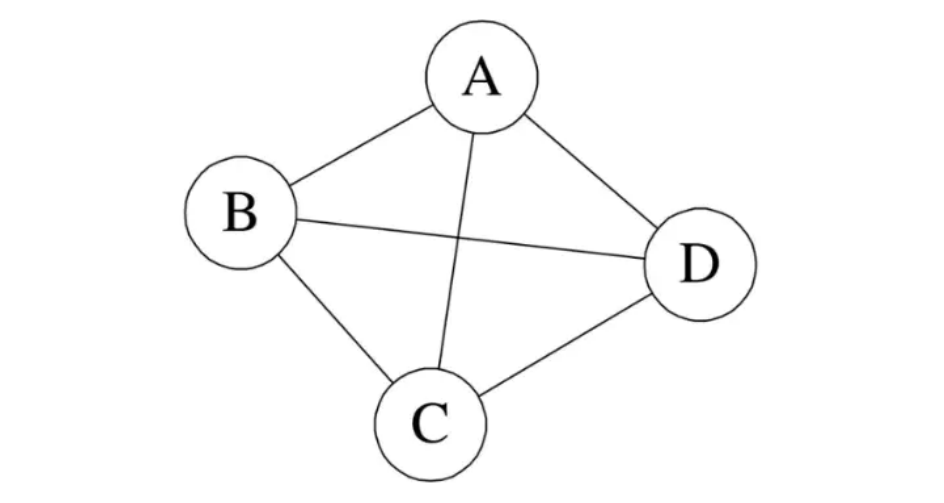
(7)强连通、强连通图、强连通分量(均为有向图中存在):
强连通:若顶点x与y之间存在可项目抵达的路径(无论是直接或间接),则称为强连通。
强连通图:图中任意俩个顶点都强连通的图。
强连通分量:即极大强连通子图。对于强连通图来说,只存在一个极大强连通子图(强连通分量)即它本身;对于非强连通图来说,存在多个极大强连通子图(即多个强连通分量),每个强连通分量都是一个强连通图。

二、图的存储
图有五种存储方式:边集数组,邻接矩阵,邻接表,十字邻接表,多重邻接表。其中十字邻接表只针对有向图,多重邻接表只针对无向图。而一般常用的是邻接矩阵和邻接表。
(1)邻接矩阵:
邻接矩阵中,存顶点采用一维数组,同时使下标相当于顶点的编号;存边采用二维数组,数组中的下标就是每个点的编号,如[i][j]意为编号为i的顶点到编号为j的顶点的边。
//用邻接矩阵存储无向带权图,则邻接矩阵存储的值可以是权值
#include<iostream>
#include <algorithm>
const int inf = 100001;//认为权值不超过10000,设置一个大点的inf用于初始化e数组,表示开始图中无边,而存储的权值代表一定有边
char v[105];//这里把顶点设置的少一点
int e[105][105];
int n, m;//顶点个数和边的个数
int find(char x);
int main()
{
std::fill(&e[0][0], &e[0][0] + 105 * 105, inf);
std::cin >> n >> m;
getchar();
for (int i = 1; i <= n; ++i)
{
std::cin >> v[i]; //存储n个顶点
}
char x, y; int w,xi, yi;
for (int i = 1; i <= m; ++i)
{
getchar();
std::cin >> x >> y >> w; //设置边和权值
xi = find(x);//查找顶点的编号
yi = find(y);
//一条无向边 相当于 俩条方向相反的有向边
e[xi][yi] = w;
e[yi][xi] = w;
}
//试图寻找一个无向图顶点的度
getchar();
std::cin >> x;
xi = find(x);
int d = 0;//度
//对于无向图临界矩阵还有个性质就是满足对称性
for (int i = 1; i <= n; ++i)
{
/*if (e[xi][i] != inf) //可以按列来找
d++;*/
if (e[i][xi] != inf) //也可以按行来找
d++;
}
std::cout << d << std::endl;
return 0;
}
int find(char x)
{
int i;
for (i = 1; i <= n; ++i)
{
if (v[i] == x)break;
}
return i;
}邻接矩阵的缺点就是不适合存稀疏图,毕竟它开的二维空间很大,如果边少,造成了浪费。
(2)邻接表:
邻接表存图的顶点采用结构体数组,数组的下标也认为是顶点编号。存边采用的是链表,即链表中存储的是以同一个顶点为弧尾到达的不同的终点的编号。
//邻接表存无向带权图
#include<iostream>
typedef struct ENode {
int adj;//终点编号
int w;//此边的权值
ENode* next;
}ENode;
struct Graph {
char data;//顶点数据
ENode* first;//以该顶点为弧尾的出边的链表
}g[105];
int n, m;
int find(char x);
int main()
{
std::cin >> n >> m;
getchar();
for (int i = 1; i <= n; ++i)
{
std::cin >> g[i].data;
g[i].first = NULL;
}
char x, y; int w, xi, yi;
for (int i = 1; i <= m; ++i)
{
getchar();
std::cin >> x >> y >> w;
xi = find(x);//查找顶点编号
yi = find(y);
//求x------》y的出边链表
ENode* e = new ENode;
e->w = w;
e->adj = yi;
e->next = g[xi].first;
g[xi].first = e; //采用的是头插法
//求y-------》x的出边链表
e = new ENode;
e->w = w;
e->adj = xi;
e->next = g[yi].first;
g[yi].first = e;
}
//求无向带权图的度
getchar();
std::cin >> x;
xi = find(x);
ENode* p = g[xi].first;
int d = 0;
while (p != NULL)
{
d++;
p = p->next;
}
std::cout << d << std::endl;
return 0;
}
int find(char x)
{
int i;
for (i = 1; i <= n; ++i)
{
if (g[i].data == x)
break;
}
return i;
}(3)十字邻接表:只适合有向图
由于邻接表存储有向图,必须要建一个出边链表(邻接表)和入边链表(逆邻接表)。而当存储一个边时,会使得这组数据信息被重复存储俩次(比如A--->B 存储的是a的出边链表和b的入边链表,而当B--->A存储的是b的出边链表和a的入边链表)。此时十字邻接表就是把邻接表和逆邻接表结合在一次,因此十字邻接表只适合有向图中。
//十字链表:只针对有向图。是对有向图存俩个链表的优化。
//即一条边只用一个结点表示,而这个结点插入到俩条链表中,这俩条链表类似相交构成十字链表。
//十字链表结点结构中有5个元素:起点(弧尾)tail,tnext指针(出边链表),终点(弧头)head,hnext(入边链表),w(权值)
//这里存储的是有向无权图
#include<iostream>
typedef struct ENode {
int tail_i;
int head_i;
struct ENode* tnext; //同弧尾的下一条边,也就是tail的下一条出边
struct ENode* hnext;//同弧头的下一条边,也就是head的下一条边
}ENode;
struct Graph {
char data;
ENode* firstOut;//出边链表
ENode* firstIn;//入边链表
}g[105];
int n, m;
int find(char x)
{
int i;
for (i = 1; i <= n; ++i)
{
if (g[i].data == x)
break;
}
return i;
}
int main()
{
std::cin >> n >> m;
getchar();
for (int i = 1; i <= n; ++i)
{
std::cin >> g[i].data;
g[i].firstIn = g[i].firstOut = NULL;//开始默认无边
}
char start, end;
for (int i = 1; i <= m; ++i)
{
getchar();
std::cin >> start >> end;
//开始插入strat的出边链表和end的入边链表
int xi = find(start);
int yi = find(end);
ENode* e = new ENode;
e->tail_i = xi;//adj记录的是出边链表的终点
e->head_i = yi;//stx记录的是入边链表的起点
e->tnext = g[xi].firstOut; //先将出边结点指针 指向 起点顶点的出边链表指针
g[xi].firstOut = e; //再将起点顶点的出边链表指针 指向 出边结点
e->hnext = g[yi].firstIn; //先将入边结点指针 指向 终点顶点的入边链表指针
g[yi].firstIn = e; //再将终点入边指针 指向 入边结点
}
int d1 = 0, d2 = 0;
getchar();
std::cin >> start;
int xi = find(start);
ENode *e = g[xi].firstOut;
while (e != NULL)
{
d1++;
e = e->tnext;
}
e = g[xi].firstIn;
while (e != NULL)
{
d2++;
e = e->hnext;
}
std::cout << "该顶点的出度为:" << d1 << " ; " << "入度为:" << d2 << std::endl;
return 0;
}(4)多重邻接表:只适合无向图
多重邻接表与十字邻接表相反,它是对无向图的邻接表的优化,也是邻接表存无向图时数组重复存储俩次,并且多重邻接表的结构和十字邻接表的结构相似。
//多重邻接表-----对无向图邻接表的优化,结构类似十字链表
#include<iostream>
typedef struct ENode {
int x_i;//端点x
int y_i;//端点y
struct ENode* xnext;//以端点x为起点的下一条边
struct ENode* ynext;//以端点y为起点的下一条边
}ENode;
struct graph {
char data;
ENode* first;
}g[105];
int n, m;
int find(char x)
{
int i;
for (i = 1; i <= n; ++i)
{
if (g[i].data == x)
break;
}
return i;
}
int main()
{
std::cin >> n >> m;
getchar();
for (int i = 1; i <= n; ++i)
{
std::cin >> g[i].data;
g[i].first = NULL;
}
char u, v; int ui, vi;
for (int i = 1; i <= m; ++i)
{
getchar();
std::cin >> u >> v;
ui = find(u);
vi = find(v);
//建立以u为起点开始的出边
ENode* e = new ENode;
e->x_i = ui;
e->xnext = g[ui].first;//xnext对应xi
g[ui].first = e;
//再连接以v为起点开始的出边
e->y_i = vi;
e->ynext = g[vi].first;//ynext对应yi
g[vi].first = e;
}
getchar();
std::cin >> u;
ui = find(u);
int d = 0;
ENode* p = g[ui].first;
while (p != NULL)
{
d++;
if (p->x_i == ui) //需要判断下一个结点的那个端点编号等于我们需要的顶点编号
{
p = p->xnext;
}
else
{
p = p->ynext;
}
}
std::cout << d << std::endl;
return 0;
}
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








