算法复杂度

文章目录

• 一、数据结构和算法
• 二、复杂度
• 三、时间复杂度
• 四、空间复杂度
• 五、大O渐近表示法
• 六、常见复杂度对比

---

前言

本文章关于数据结构和算法概念以及复杂度

---

一、数据结构和算法

       1.数据结构概念：

          数据结构是数据存储和组织的形式

          数据结构是数据存储和组织的统称

          理解：

        （1）：数据的存储，即将数据存储到内存当中，将数据存储到内存需要通过数组和链表

        （2）：数据的组织，即将数据进行增删查改

        （3）：虽然往后会学习很多的数据结构，但是数据结构存储数据底层都是通过数组和链表

                     进行存储，只是每一种数据结构使用数组和链表的方式不同，最终导致不同的数据

                     结构存储和组织数据的效率各不相同

        （4）：学习数据结构，首先明确一点：存在即合理，因为同一个数据结构面对不同场景下的

                     数据对于该数据的存储和组织的效率是不同的，所以在不同的场景下，需要不同的

                     数据结构去解决，所以我们需要根据场景去选择最适合该数据存储和组织的数据结构

       2.学习数据结构的目标

        （1）：提升理解并解决数据的能力

        （2）：提升理解数据特征的能力

        （3）：提升使用当前情况下使用最佳数据结构解决数据的能力

        （4）：提升将世界上的事物进行分解进行数据化的能力

       3.算法

         （1）：算法 == 解决问题的方法

                      算法 == 解决问题的计算步骤，最终使得问题得以解决 == 使得输入转换为输出

         （2）：面对一个问题，拥有不同的解决方法，但是不同的解决方法解决问题的效率是不同的

                      算法也是如此，面对一个问题拥有不同的算法，每种算法解决问题的效率是不同的

         （3）：面对一个问题不同的算法所需要的效率各不相同，算法是有好有坏的

                      那么如何评估一个算法的好与坏呢？

二、复杂度

           1.复杂度：

              评估一个算法好与坏的方式

            2. 因为算法在运行中是需要耗费时间资源和空间资源的

                 所以评估算法的好与坏需要通过时间和空间两个维度进行评估

                 所以复杂度就分为了时间复杂度和空间复杂度

            3.算法的时间复杂度代表着算法运行的快慢

               算法的空间复杂度代表着算法所需要的额外空间

            4.不过在当今世界更加注重算法的时间复杂度，因为随着社会的发展，内存也变得越来越

                便宜，对于空间的消耗往往就不太注重了

三、时间复杂度   

           1.时间复杂度

            （1）：时间复杂度是用来计算算法的时间效率

            （2）：算法所需要的时间是无法通过程序执行去推断的，因为编译器不同与电脑配置不同

                         所以对于同一个算法在不同的编译器上/不同的电脑上所执行的时间是不同的

                         所以这就需要我们能够在提出算法时就可以分析出算法的时间效率

           2.推导前提：

            （1）：算法中的每一条程序都会转换为对应的k（k较小）句二进制指令

            （2）：计算机一秒钟之内可以处理上亿条指令

           3.推导

             （1）：每一条代码都会被编译成k具二进制指令，但是cpu一秒中可以处理上亿条指令

                          所以每一句代码被编译的二进制指令就可以忽略看作一句代码编译成一句指令

             （2）：每一条代码被编译成一条二进制指令之后，因为cpu一秒可以执行上亿条指令

                           所以单次一条指令可以忽略不记

             （3）：那么一条代码被认为编译成一句指令，单次一句指令有忽略不计，那么需要什么

                          来得到算法的时间效率呢？

                          看哪一条代码/哪一条指令被执行了很多次 == 看循环语句/递归

             （4）：所以观察算法的时间复杂度，只需要看该算法中有多少次循环/递归

                          而循环/递归很多时候都是由参数决定的，也就是循环/递归无法

                          有一个确定的/不变的次数，而随着循环/递归的次数增加/减少，

                          算法的时间效率也在不停的变化，执行的次数就可以代表算法时间效率的优劣

                          所以算法的时间效率就可以看作一个函数式T(N)

                          自变量（N）：循环/递归的次数   因变量（T）：算法时间效率

                          函数T(N)的函数图像就代表着算法时间效率的变化趋势，就可以判断算法的优劣  

            4.算法的时间复杂度

            （1）：算法的时间复杂度是一个函数式T(N)

            （2）：函数式T(N)代表着执行次数，函数式T(N)描述着算法的运行时间

            （3）：函数是T(N)的函数图像就代表着算法时间效率的变化趋势

四、空间复杂度

           1.计算机内存单位

              位（bit）：比特位

              字节（Byte）： 1 Byte == 8 bit

              千字节（KB）： 1 KB == 1024 Byte

              兆字节（MB）： 1 MB == 1024 KB

              吉字节（GB）： 1 GB == 1024 MB

              太字节（TB）：  1 TB == 1024 GB

              拍字节（PB）：  1 PB == 1024 TB

              艾字节（EB）：  1 EB == 1024 PB

          2.内置类型大小（单位：byte）

             char：1 byte         short：2 byte           int：4 byte

             float：4 byte        double：8 byte       指针：x86环境 4 byte   x64环境下  8 byte

          3.空间复杂度 

          （1）： 空间复杂度同样也是一个函数式M(N)

          （2）： 空间复杂度函数式M(N)代表着算法在程序运行期间所需要额外临时开辟的空间

                        M(N) == 函数内部显示申请的变量的个数 && 动态申请的空间

         4.推导前提

          （1）：内存空间很庞大，但是变量所需要的空间是微小的，

                       虽然不同类型的变量所需的内存空间不一致

                       但是在内存面前，这些差异是微乎其微，这些差异可以忽略不计

          （2）：在庞大的内存面前，变量所需要的内存都可以忽略不计

          （3）：函数栈帧、函数形参、寄存器在编译时就分配好了空间，不需要将这些计算在内

          5.推导

            （1）：此时不同变量之间的差异忽略不计，变量所需要的空间也忽略不计

                         并且函数栈帧、形参、寄存器也不需要计算在内

                         那么计算算法所需要的空间，只需要计算在函数内部显示申请的额外空间即可

                       （计算函数内部显示申请的变量的个数 && 动态申请的空间）

            （2）：空间复杂度计算的不是程序所需要多少byte

                        计算的是在程序内部显示申请了多少个变量 && 动态申请的空间

五、大O渐近表示法

          1.时间复杂度和空间复杂度的表示方法都采用大O渐近表示法

          2.大O渐近表示法规则：

          （1）：去除低阶项，只保留高阶项

                       原因：随着N（自变量）不断增大，函数的趋势由高阶项主导

                       低阶项的影响微乎其微，所以就将低阶项去除

          （2）：高阶项系数不为1时，将高阶项系数改为1

                       原因：随着N（自变量）不断增大，高阶项的系数无论是多少

                       对于函数整体趋势来说没有影响

          （3）：如果此时复杂度的结果只有常数没有N（自变量），那么将整体改为1

                       原因：此时函数式之中只有常数项，也就是常数函数

                       随着自变量不断变化，常数函数的因变量是不会产生任何变化的

                       函数图像就是一条关于x轴平行的直线，函数的趋势一层不变

                       跟1时是平行的，那不如全部统一起来，函数式中只有常数，整体改为1

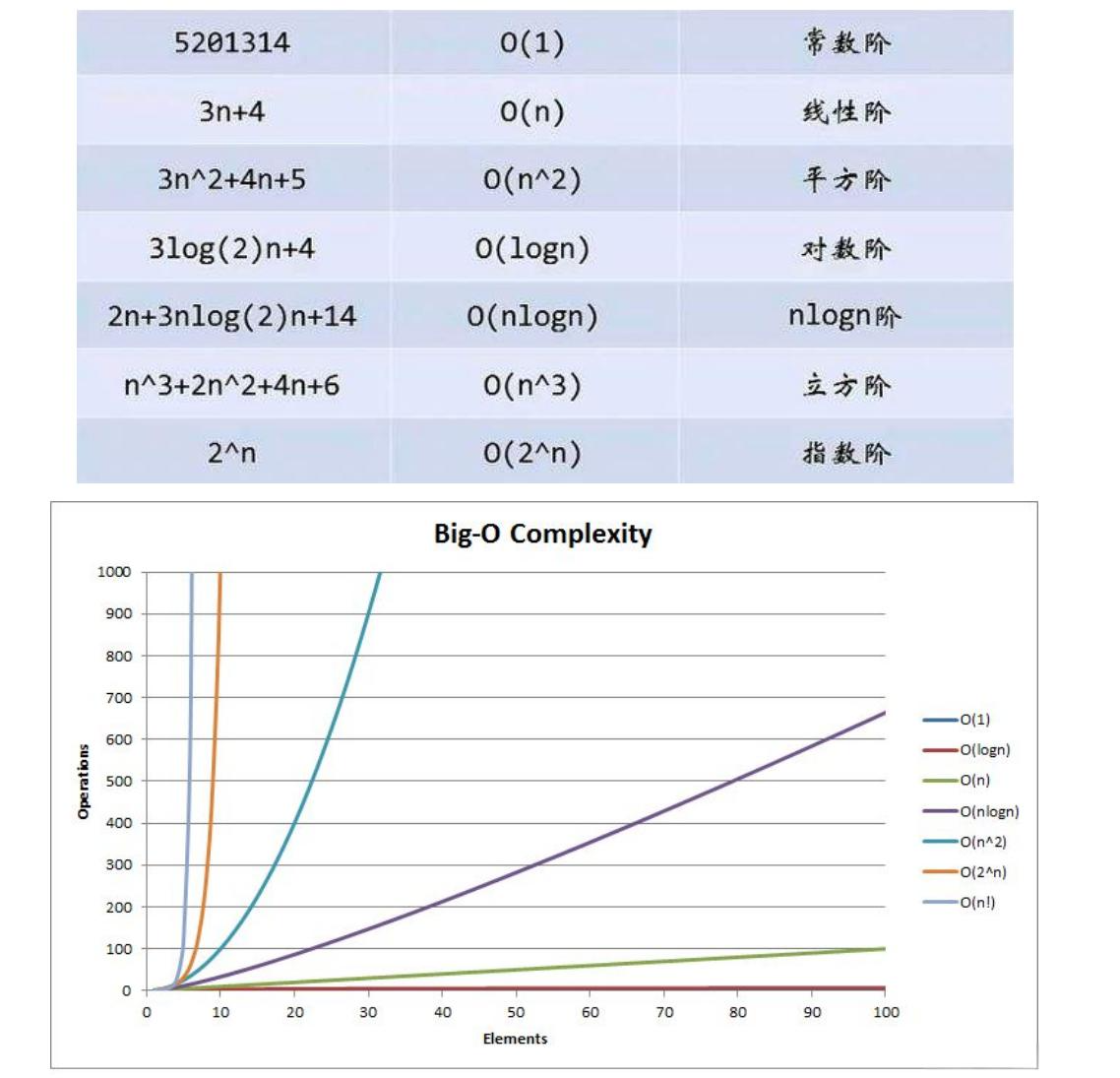
六、常见复杂度对比