Transformer模型注意力机制详解-CSDN博客

本文链接：https://blog.csdn.net/2402_84226753/article/details/147719444

在人工智能的发展长河中，序列数据处理始终是核心挑战之一。无论是人类语言的字词句段，还是图像中的像素序列、视频里的帧间关联，亦或是金融市场的时间序列数据，都需要模型具备理解长距离依赖关系的能力。传统的循环神经网络（RNN）曾被寄予厚望，但其天生的序列化处理特性导致难以并行计算，且在面对超长序列时不可避免地出现梯度消失问题，就像一个记忆力有限的学习者，难以把握远距离的关键信息。

一、引言

在数据爆炸式增长的今天，传统模型的线性计算复杂度已难以应对 TB 级的序列数据，而 Transformer 的并行计算特性使其算力利用率提升数个量级；当任务需求从简单分类转向复杂生成（如文本创作、图像生成），其强大的上下文建模能力成为刚需；尤其是在多模态融合趋势下，注意力机制天然的跨维度关联能力，让不同模态的数据能在统一框架下实现深度交互。可以说，Transformer 的出现不仅是技术迭代的必然结果，更是应对智能时代数据复杂性的必要选择。

本文将沿着技术演进的脉络，从注意力机制的核心原理出发，拆解 Transformer 的架构设计，揭示其如何通过自注意力、多头机制和位置编码实现序列建模的革命性突破。

二、自注意力机制

Transformer的核心思想是采用自注意 （self-attention）对序列进行建模：对于输入序列 $X$ 中的每一个元素 $x_{i}$ ，都生成一个自注意力编码 $h^{SA}_{i}$ ，即 $H^{SA}=f_{SA}(X,\theta )$ 。具体计算过程如下：

1.对于每一个词 $x_{i}$ ，通过线性变化生成3个向量 $k_{i},q_{i},v_{i}=[W_{k}x_{i},W_{q}x_{i},W_{v}x_{i}]$ ，分别表示关键字（key）（一些资料里也称作键）、询问（query）和值（value）。这里的 $W_{k},W_{q},W_{v}$ 均为可学习的参数。

这里提取关键字、询问和值的目的是希望这3个变量能够提取出输入向量 $x_{i}$ 中的不同信息，帮助注意力计算。

2.接着计算注意力权重 $\alpha_{i}=Softmax(\beta _{i})$ ，其中 $\beta _{i,j}=q_{i}^{T}k_{j}$ （当前词 $x_{i}$ 的询问向量与被注意词 $x_{j}$ 的关键字向量的内积），故 $\alpha _{i,j}=\frac{exp(q^{T}_{i}k_{j})}{\sum _{j}exp(q^{T}_{i}k_{j})}$ ，表示输入向量 $x_{i}$ 对于向量 $x_{j}$ 的注意力大小。

3.输出注意力向量为 $h_{i}^{SA}=\alpha _{i}^{T}V=\sum _{j}\alpha_{i,j}v_{j}$ ，即值向量的加权平均。

下图展示了Transformer中的自注意力机制对于输入序列 $x_{1},x_{2},x_{3}$ 进行编码计算的一个例子。

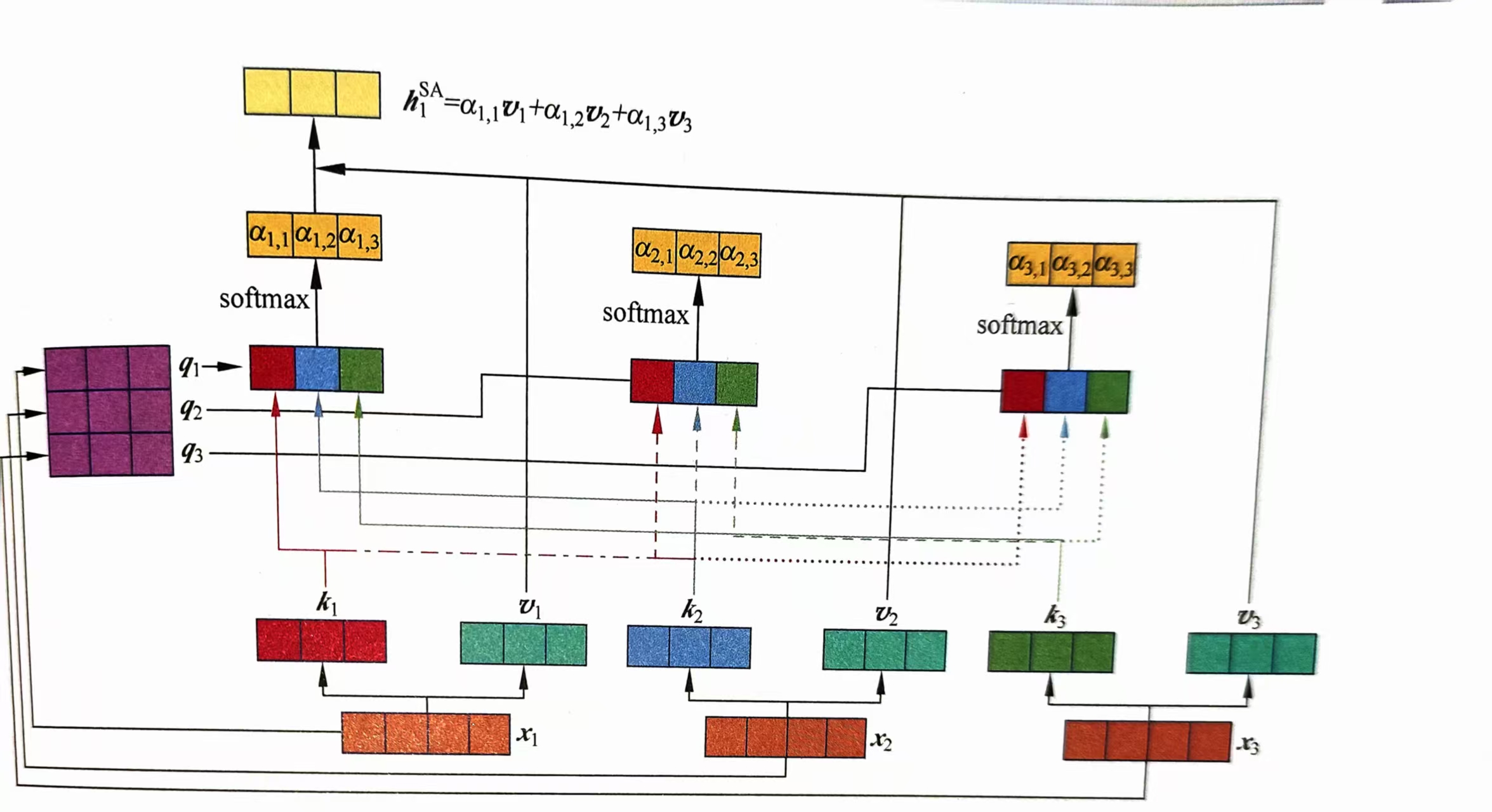
在这里我们也可以堆叠多层自注意力机制模块，实现更好的表征计算。最后，如果希望得到整个句子的编码，可以简单的对所有的输出向量取平均，即 $h^{SA}=\frac{1}{N}\sum _{i}h_{i}^{SA}$ ，或者单独定义一个特别的可学习向量 $x_{0}$ 加入到序列 $X$ 中，然后采用 $x_{0}$ 对应的自注意输出向量 $h_{0}^{SA}$ ，作为最后的句子的编码。

三、多头注意力机制

经典的注意力机制计算中，对于每一个输入词 $x_{i}$ ，只对应唯一的注意力权重 $\alpha _{i}$ 。但是同一句子中，可能有多个部分需要分别被注意到。因此，Transformer引入多头注意力（multi-head attention）。即对于当前词 $x_{i}$ 的 $d$ 维度的特征向量 $k_{i},q_{i},v_{i}\in R^{d}$ ，将其切割成 $m$ 个长度为 $\frac{d}{m}$ 的子向量，并计算对应的 $m$ 个注意力权重 $\alpha_{i}^{1},\alpha_{i}^{2},.....\alpha_{i}^{m}$ 。

具体而言，将 $k_{i},q_{i},v_{i}$ 切割成的第 $l$ 个子向量记作 $k_{i}^{l},q_{i}^{l},v_{i}^{l}$ ，则 $\alpha _{i,j}^{l}=\frac{exp((q^{l}_{i})^{T}k_{j}^{l})}{\sum _{j}exp((q^{l}_{i})^{T}k_{j}^{l})}$ 。同样的，也可以得到 $m$ 个长度较短的注意力向量 $h_{i}^{SA^{l}}=\sum _{j}\alpha_{i,j}^{l}v_{j}^{l}$ ，将其拼接起来就可以得到完整的注意力向量 $h_{i}^{SA}=concat(h_{i}^{SA^{l}}.....h_{i}^{SA^{m}})$ 。多头注意力机制可以使不同的注意力权重 $\alpha^{l}$ 关注句子中的不同的成分，以进一步提高自注意力机制的表达能力。

随着向量维度 $d$ 的增大，向量内积 $q_{i}^{T}k_{j}$ 的内积也会随之变大，对应的导数也会不断变大，并最终导致模型训练不稳定。因此，Transformer模型使用维度对内积进行调整，即计算 $\alpha_{i}=Softmax(\frac{q_{i}^{T}k_{j}}{\sqrt{d}})$ 来稳定模型训练。同样，在多头注意力机制中，即 $\alpha_{i}^{l}=Softmax(\frac{q_{i}^{l^{T}}k_{j}^{l}}{\sqrt{\frac{d}{m}}})$ 。这个技术也被称作Scaled Dot Product。感兴趣的读者可以进一步的了解和学习。

四、非线性层设计

在上面的自注意力机制介绍中，除了计算注意力权重 $\alpha_{i}$ 的时候使用到了 $Softmax$ 函数，其他所有计算都是线性的。神经网络中，非线性层承担着关键角色，为模型赋予强大的表达能力，使其能学习到复杂的模式与关系。

因此，在通过自注意力得到每个词的表示向量 $h_{i}^{SA}$ 后，我们采取另一个 $MLP$ 层对其进行编码。在Transformer中还引入了残差连接和层归一化来提高模型深度加深后的训练稳定性，最终得到的关于 $x_{i}$ 的编码向量 $h_{i}^{out}$ 的计算如下：

${h_{i}}'=LayerNorm(h_{i}^{SA}+x_{i})$

$h_{i}^{out} = LayerNorm[W_{2}\cdot ReLU(W_{1}\cdot{h_{i}}'+b_{1})+b_{2}]$

其中 $W_{1},W_{2},b_{1},b_{2}$ 均为训练参数。

引入 ReLU 这样的非线性激活函数后，模型能够拟合任意复杂的函数，极大增强了 Transformer 对自然语言、图像等复杂数据的建模能力。在自然语言处理任务中，它可以捕捉到词汇间错综复杂的语义关联，例如在处理 “苹果从树上掉落” 这样的句子时，通过非线性层，模型能够深入理解 “苹果” 与 “掉落”“树上” 之间并非简单线性的语义依赖，从而更好地完成语义分析、文本生成等任务。

五、位置编码

根据以上的关于自注意力机制的计算，我们可以知道如下结论：根据 $h_{i}^{SA}$ 的计算方式，不管输入序列 $x_{1},x_{2}....x_{N}$ 按照何种顺序排列， $h_{i}^{SA}$ 的计算结果都是不变的。也就是说，自注意力机制的一个重要的特点为输入词序是顺序无关的。

但是，对于自然语言处理任务而言，词的顺序是非常重要的。比如“苹果在树上”和“树在苹果上” 是完全不同的意义，为了能够使自注意力机制可以有效的处理有序数据，需要将位置信息引入模型。

具体而言，对于处在序列中第 $i$ 个位置的词 $x_{i}$ 引入位置编码 $p_{i}$ ，表示位置下标 $i$ 的特征，并把 $[x_{i},p_{i}]$ 一起作为自注意力模块的输入特征。对于 $p_{i}$ 的具体内容，可以选择让模型对于不同的位置 $i$ ，自动学习位置编码 $p_{i}$ ，即把 $p_{i}$ 视为模型参数，这也被称为可学习的位置编码。可学习的位置编码的优点是表达能力强、编写简单、计算速度快，但是必须对任意的位置 $i$ 都单独学习一个编码，因此训练时必须预先设定好位置下标的最大范围 $N$ ，且在测试的时候也只能处理长度最多为 $N$ 的序列，泛化能力有限。

针对这个现象，另一种可行的方案叫做相对位置编码。在计算注意力权重的时候引入相对距离的特征向量 $p_{[i-j]}$ ，即 $\alpha_{i}=Softmax(q_{i}^{T}(k_{j}+p_{[i-j]}))$ 。其中， $p_{[i-j]}$ 为相对距离 $i-j$ 对应的位置编码向量（这里的相对距离可正可负），实际应用中，一般会设置一个最大的相对位置 $\delta_{max}$ ：若 $\left | i-j \right |>\delta _{max}$ ，则直接使用 $p_{-\delta _{max}}$ 或者 $p_{\delta _{max}}$ 。这是因为在实践中，距离很远的两个词之间的相对位置信息往往不需要那么精确，也普遍不重要。

这里再介绍一下Transformer论文中的一种方法——基于三角函数的绝对位置编码方法。这里用 $d$ 来表示位置编码 $p_{i}$ 的维度，则计算如下：

$p_{i}=\left\{\begin{matrix} sin(i/10000^{2\times 1/d})\\ cos(i/10000^{2\times1/d})\\ \bullet \\ \bullet\\ \bullet\\ sin(i/10000^{2\times \frac{d}{2}/d})\\ cos(i/10000^{2\times\frac{d}{2}/d})\\ \end{matrix}\right.$

该位置编码方式的优点如下：首先由于三角函数是周期变化的，理论上泛化性得到了保证，即对于任意的 $i$ 都可以直接的计算出其位置编码，同时通过内积图显示出来，如下图所示。通过三角函数编码，相对距离较近的位置编码的内积较大，这也从某种程度上简介的反映出了相对位置的关系。当然，由于这种方法不包含任何的可学习参数，实际使用中的效果可能会比可学习的位置编码方法要差。同时如果在测试时遇到比训练数据要长很多的序列，其实际的泛化表现会远差于相对位置的编码方法。

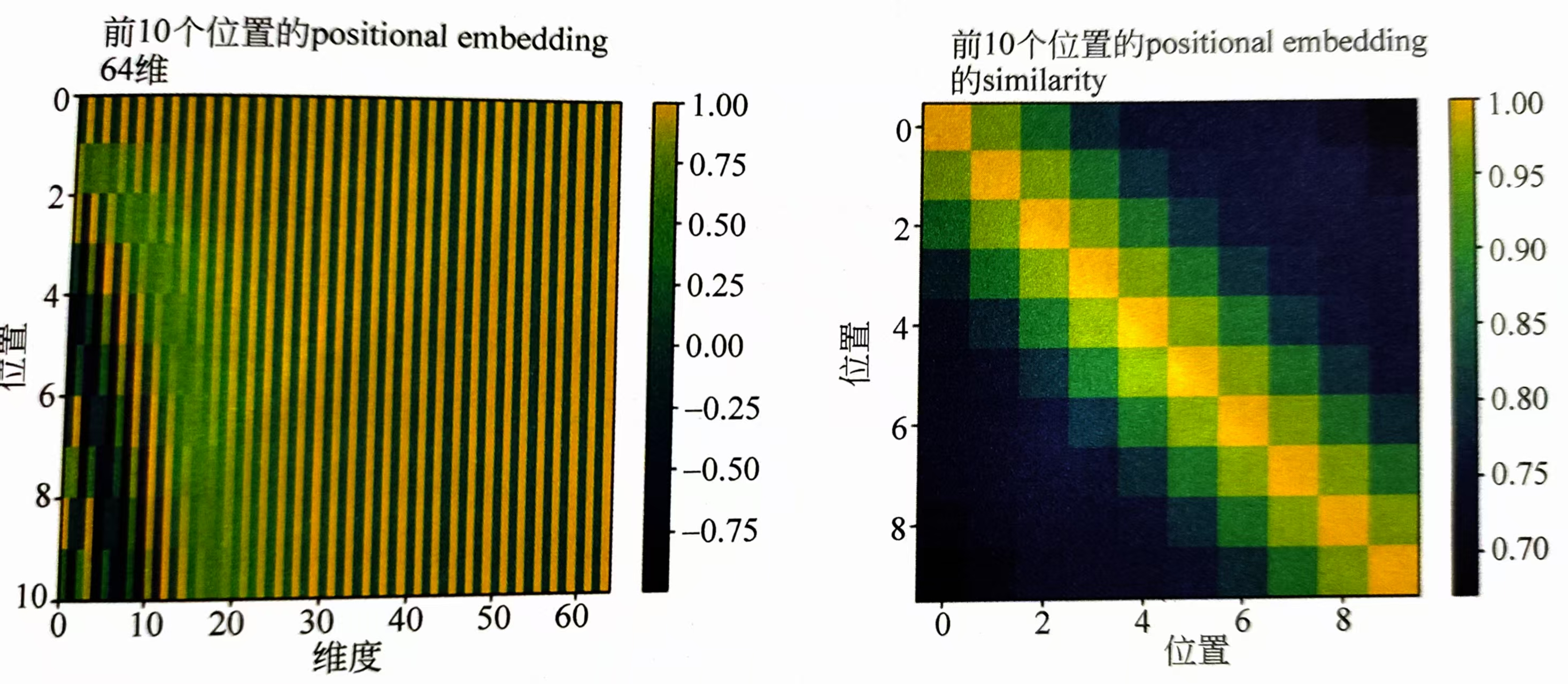
综上所述，三种位置编码方法各有优缺点，因此在实际的使用过程中可以根据问题的困难程度以及训练和测试的时间效率要求选择合适的方法。

六、掩码注意力机制

现在我们通过位置编码和自注意力，可以将输入序列 $X$ 进行编码。但是如何解码呢？即，给定特征向量 $h$ 和已生成的前缀 $y_{1},y_{2}...y_{t-1}$ ，如何使用自注意力机制生成 $y_{t}$ 呢？在经典的自注意力机制中，每个词都会与任意其他的词两两内积得到注意力向量。然而在语言模型生成时，由于 $y_{1},y_{2}...y_{t}$ 是顺序生成的，因此词 $y_{i}$ 只能对位置更靠前的词 $y_{j<i}$ 计算注意力权重，即，对任意 $j>i$ ，都有 $\alpha_{i,j}=0$ 。

这里的意思是，在编码的时候，输入的序列是一次性输入的，也就是说模型能够一次窥见所有的词，从而对于任意位置的词都能计算并表示出其相对的注意力大小；但是在模型输出的时候，由于模型是一个词一个词输出的，对于当前输出的词只能计算已经输出的词，也就是位置更靠前的词的相对注意力大小，对于位置靠后的词（因为还没有输出），所以都有 $\alpha_{i,j}=0,j > i$ 。

实际操作中，Transformer在计算注意力权重时引入了 $N \times N$ 的0/1掩码矩阵 $M$ ，表示位置 $i$ 是否需要对位置 $j$ 进行注意力计算，即

$\alpha_{i}=Softmax[q_{i}^{T}\cdot M-\infty \cdot(1-M)]$

这里把 $M_{i,j}$ 为0的 $i,j$ 对应的注意力机制权重 $\alpha_{i,j}$ 自动设置为0。在编码时，把 $M$ 设置为全1矩阵；在解码时，把 $i<j$ 的位置设置为 $M_{i,j}=0$ 即可。这种采用掩码的自注意力计算方式称为掩码注意力机制（masked attention）。同时，掩码矩阵的存在可以使得在训练过程中保持自注意力计算高度并行的前提下（可以使用GPU加速），满足序列生成的依赖。

以上就是对于Transformer的架构的一些简单的介绍和梳理。Transformer 基于自注意力机制，具备高效并行计算、长距离依赖建模能力，结构灵活适配多任务，广泛应用于自然语言处理（翻译、生成）、计算机视觉（分类、检测）及跨模态领域（图文生成、多模态推理），是现代 AI 核心架构。感兴趣的读者可以阅读Transformer原论文进一步学习，也可以寻找开源项目进行实战练习。

参考资料：人工智能（姚期智主编）