图论day57|101.孤岛的总面积(卡码网)【逆向思维】 、102.沉没孤岛(卡码网)、103.水流问题(卡码网)【逆向思维】
101.孤岛的总面积(卡码网)
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要计算所有孤岛的总面积,岛屿面积的计算方式为组成岛屿的陆地的总数。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0。
输出描述
输出一个整数,表示所有孤岛的总面积,如果不存在孤岛,则输出 0。
输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
1
提示信息
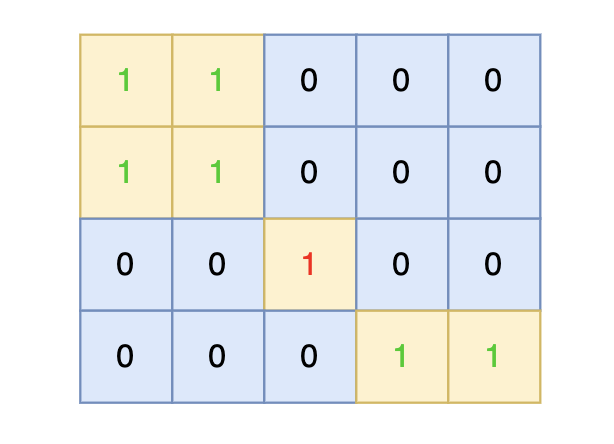
在矩阵中心部分的岛屿,因为没有任何一个单元格接触到矩阵边缘,所以该岛屿属于孤岛,总面积为 1。
数据范围:
1 <= M, N <= 50。
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int count=0;
int dir[4][2]={1,0,-1,0,0,1,0,-1};
void bfs(vector<vector<int>> &grid,int x,int y)
{
queue<pair<int,int>> que;
que.push({x,y});
grid[x][y]=0;
count++;
while(!que.empty())
{
pair<int,int> cur=que.front();
que.pop();
int curx=cur.first;
int cury=cur.second;
for(int i=0;i<4;i++)
{
int nextx=curx+dir[i][0];
int nexty=cury+dir[i][1];
if(nextx<=0||nextx>=grid.size()||nexty<=0||nexty>=grid[1].size())
continue;
if(grid[nextx][nexty]==1)
{
que.push({nextx,nexty});
count++;
grid[nextx][nexty]=0;
}
}
}
}
int main()
{
int n,m;
cin>>n>>m;
vector<vector<int>> grid(n+1,vector<int>(m+1,0));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>grid[i][j];
for(int i=1;i<=n;i++)
{
if(grid[i][1]==1) bfs(grid,i,1);
if(grid[i][m]==1) bfs(grid,i,m);
}
for(int j=1;j<=m;j++)
{
if(grid[1][j]==1) bfs(grid,1,j);
if(grid[n][j]==1) bfs(grid,n,j);
}
count=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(grid[i][j]==1)
bfs(grid,i,j);
cout<<count<<endl;
}
分析过程如下:

102.沉没孤岛(卡码网)
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要将所有孤岛“沉没”,即将孤岛中的所有陆地单元格(1)转变为水域单元格(0)。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。
之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出将孤岛“沉没”之后的岛屿矩阵。 注意:每个元素后面都有一个空格
输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
1 1 0 0 0
1 1 0 0 0
0 0 0 0 0
0 0 0 1 1
提示信息
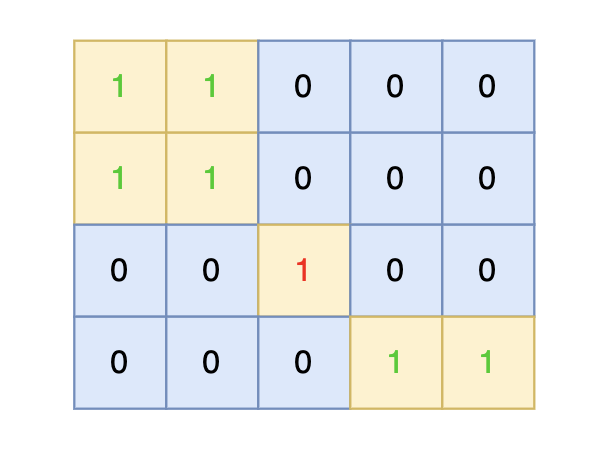
将孤岛沉没。
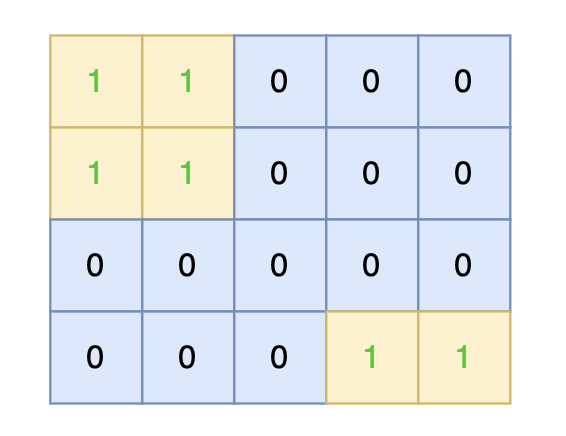
数据范围:
1 <= M, N <= 50。
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int dir[4][2]={1,0,-1,0,0,1,0,-1};
void bfs(vector<vector<int>> &grid,int x,int y)
{
queue<pair<int,int>> que;
que.push({x,y});
grid[x][y]=0;
while(!que.empty())
{
pair<int,int> cur=que.front();
que.pop();
int curx=cur.first;
int cury=cur.second;
for(int i=0;i<4;i++)
{
int nextx=curx+dir[i][0];
int nexty=cury+dir[i][1];
if(nextx<=0||nextx>=grid.size()||nexty<=0||nexty>=grid[1].size())
continue;
if(grid[nextx][nexty]==1)
{
que.push({nextx,nexty});
grid[nextx][nexty]=0;
}
}
}
}
int main()
{
int n,m;
cin>>n>>m;
vector<vector<int>> grid(n+1,vector<int>(m+1,0));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>grid[i][j];
vector<vector<int>> grid0=grid;
for(int i=1;i<=n;i++)
{
if(grid[i][1]==1) bfs(grid,i,1);
if(grid[i][m]==1) bfs(grid,i,m);
}
for(int j=1;j<=m;j++)
{
if(grid[1][j]==1) bfs(grid,1,j);
if(grid[n][j]==1) bfs(grid,n,j);
}
vector<vector<int>> grid1(n+1,vector<int>(m+1,0));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(grid[i][j]==1)
grid1[i][j]=0;
else if(grid[i][j]==0)
grid1[i][j]=1;
}
vector<vector<int>> grid2(n+1,vector<int>(m+1,0));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(grid0[i][j]==1&&grid1[i][j]==1)
grid2[i][j]=1;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m-1;j++)
{
cout<<grid2[i][j]<<" ";
}
cout<<grid2[i][m]<<endl;
}
}

103.水流问题(卡码网)
题目描述
现有一个 N × M 的矩阵,每个单元格包含一个数值,这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界,而矩阵的右边界和下边界被视为第二组边界。
矩阵模拟了一个地形,当雨水落在上面时,水会根据地形的倾斜向低处流动,但只能从较高或等高的地点流向较低或等高并且相邻(上下左右方向)的地点。我们的目标是确定那些单元格,从这些单元格出发的水可以达到第一组边界和第二组边界。
输入描述
第一行包含两个整数 N 和 M,分别表示矩阵的行数和列数。
后续 N 行,每行包含 M 个整数,表示矩阵中的每个单元格的高度。
输出描述
输出共有多行,每行输出两个整数,用一个空格隔开,表示可达第一组边界和第二组边界的单元格的坐标,输出顺序任意。
输入示例
5 5
1 3 1 2 4
1 2 1 3 2
2 4 7 2 1
4 5 6 1 1
1 4 1 2 1
输出示例
0 4
1 3
2 2
3 0
3 1
3 2
4 0
4 1
提示信息
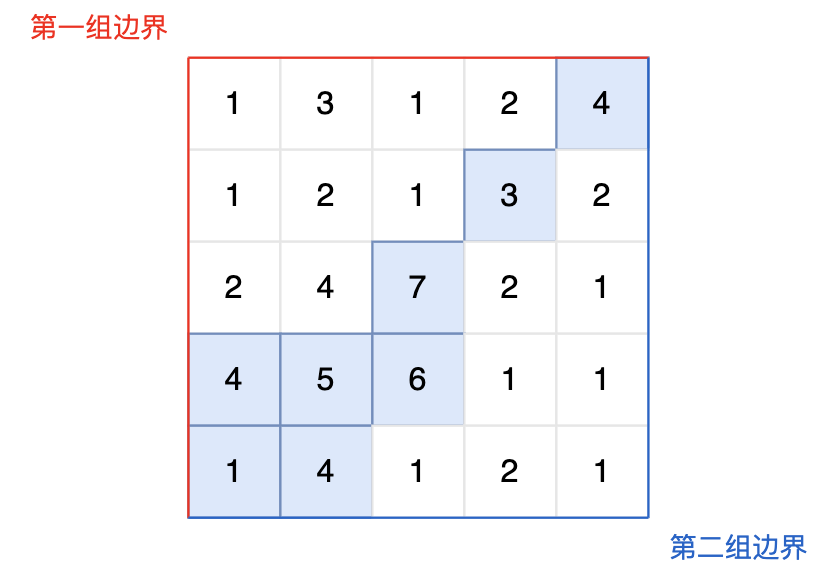
图中的蓝色方块上的雨水既能流向第一组边界,也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。
数据范围:
1 <= M, N <= 100。
1.常规思维
具体代码来自卡哥,时间复杂度是O(m2*n2):
#include <iostream>
#include <vector>
using namespace std;
int n, m;
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
// 从 x,y 出发 把可以走的地方都标记上
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
if (visited[x][y]) return;
visited[x][y] = true;
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue;
if (grid[x][y] < grid[nextx][nexty]) continue; // 高度不合适
dfs (grid, visited, nextx, nexty);
}
return;
}
bool isResult(vector<vector<int>>& grid, int x, int y) {
vector<vector<bool>> visited(n, vector<bool>(m, false));
// 深搜,将x,y出发 能到的节点都标记上。
dfs(grid, visited, x, y);
bool isFirst = false;
bool isSecond = false;
// 以下就是判断x,y出发,是否到达第一组边界和第二组边界
// 第一边界的上边
for (int j = 0; j < m; j++) {
if (visited[0][j]) {
isFirst = true;
break;
}
}
// 第一边界的左边
for (int i = 0; i < n; i++) {
if (visited[i][0]) {
isFirst = true;
break;
}
}
// 第二边界右边
for (int j = 0; j < m; j++) {
if (visited[n - 1][j]) {
isSecond = true;
break;
}
}
// 第二边界下边
for (int i = 0; i < n; i++) {
if (visited[i][m - 1]) {
isSecond = true;
break;
}
}
if (isFirst && isSecond) return true;
return false;
}
int main() {
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
// 遍历每一个点,看是否能同时到达第一组边界和第二组边界
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (isResult(grid, i, j)) {
cout << i << " " << j << endl;
}
}
}
}
2.逆向思维
时间复杂度为O(n*m)
#include <iostream>
#include <vector>
using namespace std;
int dir[4][2]={1,0,-1,0,0,1,0,-1};
void dfs(vector<vector<int>> grid,vector<vector<bool>> &visited,int x,int y)
{
if(visited[x][y])
return;
visited[x][y]=true;
for(int i=0;i<4;i++)
{
int nextx=x+dir[i][0];
int nexty=y+dir[i][1];
if(nextx<=0||nextx>=grid.size()||nexty<=0||nexty>=grid[1].size())
continue;
if(grid[nextx][nexty]<grid[x][y])
continue;
dfs(grid,visited,nextx,nexty);
}
}
int main()
{
int n,m;
cin>>n>>m;
vector<vector<int>> grid(n+1,vector<int>(m+1,0));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>grid[i][j];
vector<vector<bool>> firstVisited(n+1,vector<bool>(m+1,false));
vector<vector<bool>> secondVisited(n+1,vector<bool>(m+1,false));
for(int i=1;i<=n;i++)
{
dfs(grid,firstVisited,i,1);
dfs(grid,secondVisited,i,m);
}
for(int j=1;j<=m;j++)
{
dfs(grid,firstVisited,1,j);
dfs(grid,secondVisited,n,j);
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(firstVisited[i][j]&&secondVisited[i][j])
cout<<i-1<<" "<<j-1<<endl;
}
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








