【算法笔记】有人看海，有人被爱，有人做不出 leetcode 第一题（栈与队列专题）-CSDN博客

本文链接：https://blog.csdn.net/2402_84916296/article/details/147729856

在这里插入图片描述

Day9: 栈与队列

栈：适合处理后进先出的场景，如函数调用栈、括号匹配等。
队列：适合处理先进先出的场景，如任务调度、消息队列等。

用栈实现队列

题目链接：232. 用栈实现队列 - 力扣（LeetCode）

文章讲解：代码随想录

视频讲解：栈的基本操作！ | LeetCode：232.用栈实现队列_哔哩哔哩_bilibili

题目建议：大家可以先看视频，了解一下模拟的过程，然后写代码会轻松很多。

class MyQueue {

    public MyQueue() {
        
    }
    
    public void push(int x) {
        
    }
    
    public int pop() {
        
    }
    
    public int peek() {
        
    }
    
    public boolean empty() {
        
    }
}

题目解析

使用栈来模拟队列的行为，如果仅仅用一个栈，是一定不行的，因为出栈和出队列的顺序相反，所以需要两个栈一个输入栈，一个输出栈，这里要注意输入栈和输出栈的关系。

完整代码

在这里插入图片描述

用队列实现栈

题目链接：225. 用队列实现栈 - 力扣（LeetCode）

文章讲解：代码随想录

视频讲解：队列的基本操作！ | LeetCode：225. 用队列实现栈_哔哩哔哩_bilibili

题目建议：可能大家惯性思维，以为还要两个队列来模拟栈，其实只用一个队列就可以模拟栈了。建议大家掌握一个队列的方法，更简单一些，可以先看视频讲解

class MyStack {

    public MyStack() {
        
    }
    
    public void push(int x) {
        
    }
    
    public int pop() {
        
    }
    
    public int top() {
        
    }
    
    public boolean empty() {
        
    }
}

题目解析

使用一个队列模拟栈，在出栈时，可以把 n-1 个元素先出队列再入队列，此时出队列的元素，就是栈要弹出的元素；

使用两个队列来模拟栈，只不过没有输入和输出的关系，而是其中一个队列用于备份！

用两个队列 que1 和 que2 实现队列的功能，que2 其实完全就是一个备份的作用：

把que1 最后面的元素以外的元素都备份到que2；
然后弹出最后面的元素；
再把其他元素从 que2 导回 `que1。

完整代码

方法一：使用单队列循环

在这里插入图片描述

方法二：使用双队列来保证队列顺序与栈一致

在这里插入图片描述

有效的括号

题目链接：20. 有效的括号 - 力扣（LeetCode）

文章讲解：代码随想录

视频讲解：栈的拿手好戏！| LeetCode：20. 有效的括号_哔哩哔哩_bilibili

题目建议：讲完了栈实现队列，队列实现栈，接下来就是栈的经典应用了。大家先自己思考一下有哪些不匹配的场景，在看视频我讲的都有哪些场景，落实到代码其实就容易很多了。

class Solution {
    public boolean isValid(String s) {
        
    }
}

题目解析

栈结构适合解决对称匹配问题。在处理括号匹配问题时，首先要分析不匹配的三种情况：

左括号多余：字符串中左括号数量多于右括号，导致无法完全匹配。

右括号多余：字符串中右括号数量多于左括号，或者右括号出现在没有匹配左括号的情况下。

括号顺序错误：左括号和右括号的顺序不正确，例如“)(”这种情况。

在写代码之前，明确这些不匹配情况，可以避免逻辑混乱，提高代码的准确性和可读性。

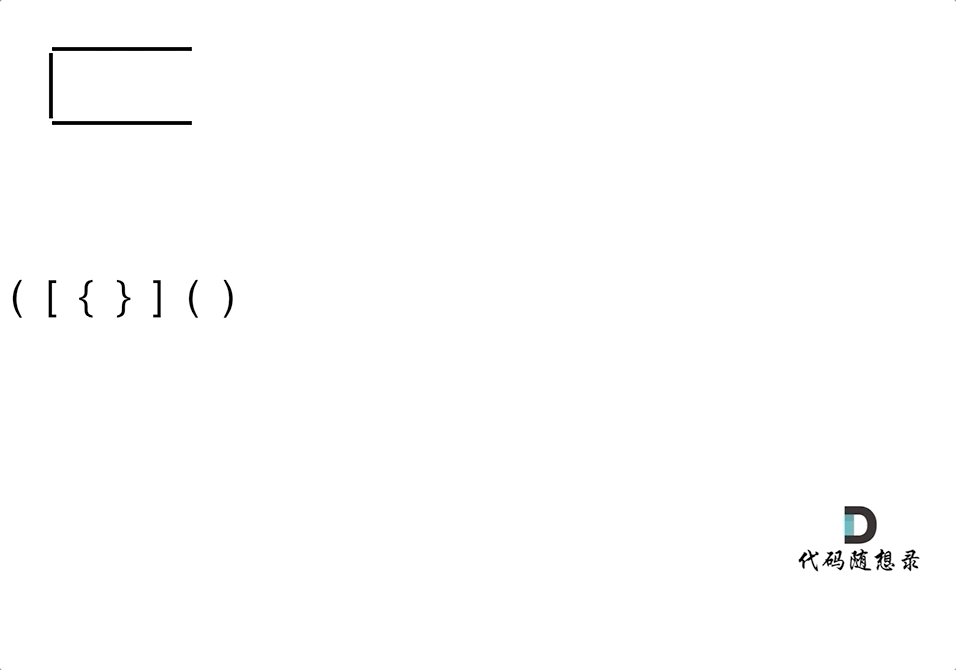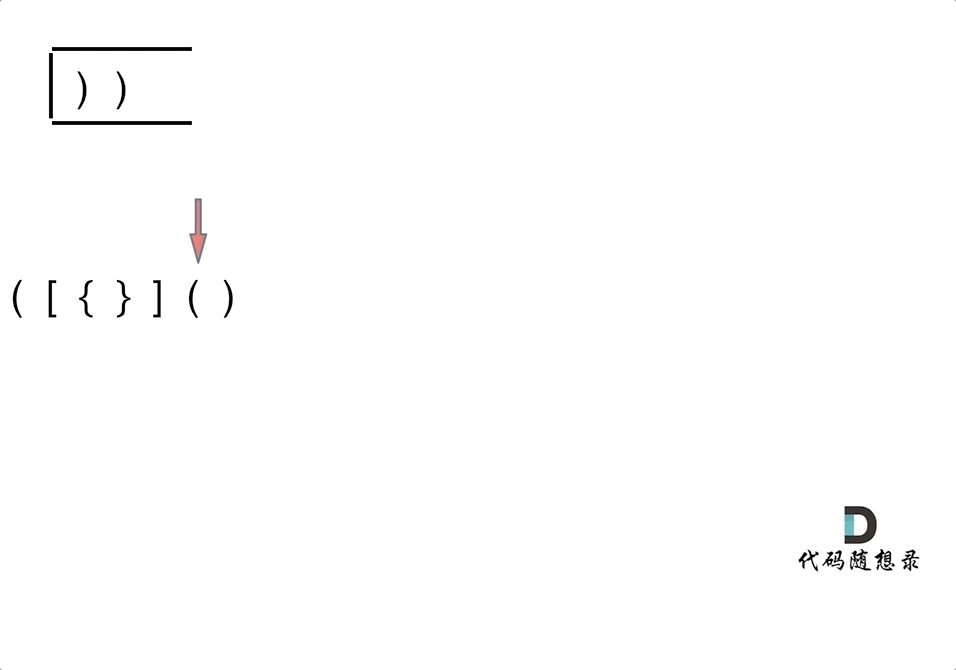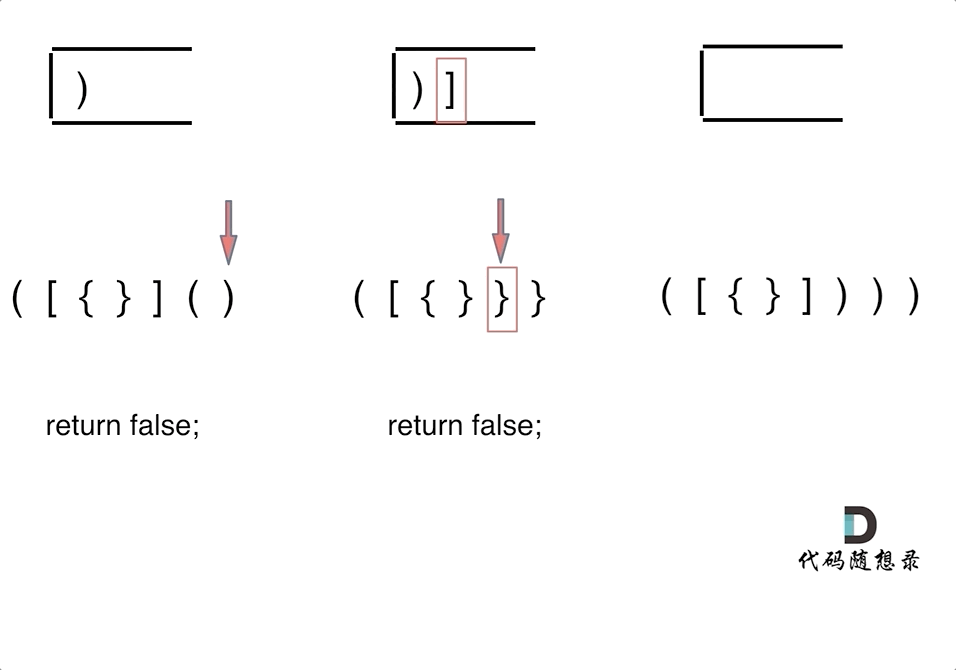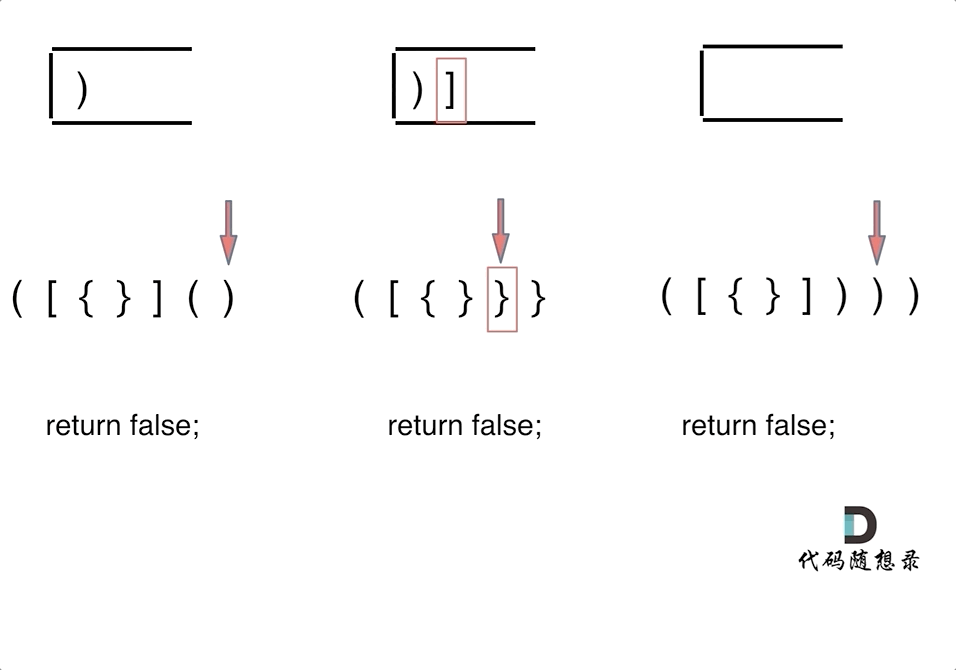
完整代码

在这里插入图片描述

删除字符串中的所有相邻重复项

题目链接：1047. 删除字符串中的所有相邻重复项 - 力扣（LeetCode）

文章讲解：代码随想录

视频讲解：栈的好戏还要继续！| LeetCode：1047. 删除字符串中的所有相邻重复项_哔哩哔哩_bilibili

题目建议：栈的经典应用。要知道栈为什么适合做这种类似于爱消除的操作，因为栈帮助我们记录了遍历数组当前元素时候，前一个元素是什么。

class Solution {
    public String removeDuplicates(String s) {
        
    }
}

题目解析

本题是删除相邻重复元素的问题，可以用栈解决。具体思路如下：

栈的作用：栈用于存放遍历过的元素，目的是判断当前元素是否与栈顶元素相邻且相同。
匹配与消除：如果当前元素与栈顶元素相同，则弹出栈顶元素，实现消除操作；否则，将当前元素压入栈。
生成结果：遍历结束后，栈中剩余的元素组成字符串，但需反转顺序以恢复正序，最终得到结果。

总结：通过栈存储遍历过的元素，实现相邻重复项的匹配与消除，最后反转栈中剩余元素得到最终结果。

那么，我们是否可以使用快慢双指针，来模拟栈的操作呢？

slow模拟操作栈指针，fast 模拟遍历数组指针

s[++slow] = s[fast] 模拟入栈操作，slow-- 模拟出栈操作

完整代码

方法一：栈

在这里插入图片描述

方法二：使用快慢双指针模拟栈操作

class Solution {
    public String removeDuplicates(String ss) {
        Stack<Character> stack = new Stack<>();
        char[] s = ss.toCharArray();
        stack.push(s[0]);
        for (int i = 1; i < s.length; i++) {
            if (!stack.isEmpty() && s[i] == stack.peek()) {
                stack.pop();
                continue;
            }
            stack.push(s[i]);
        }
        int size = stack.size();
        char[] ret = new char[size];
        for (int i = size - 1; i >= 0; i--) {
            ret[i] = stack.pop();
        }
        return new String(ret);
    }
}

class Solution {
    public String removeDuplicates(String ss) {
        int slow = -1; // -1 模拟栈空的情况
        char[] s = ss.toCharArray();
        s[++slow] = s[0];  
        for (int fast = 1; fast < s.length; fast++) { // 有循环条件, 无须担心只有一个元素的情况造成的越界
            if (slow != -1 && s[fast] == s[slow]) {
                // 关键err: 重复, slow--，模拟栈抛出栈顶元素
                slow--;
                continue;
            }
            // 关键err: 未重复, slow 模拟入栈元素
            s[++slow] = s[fast];
        }
        return new String(Arrays.copyOf(s, slow + 1));  // err: 此时 slow 模拟的是栈元素个数, slow+1 才能来到需要拷贝数组的地方
    }
}

在这里插入图片描述

Day10 栈与队列

逆波兰表达式求值

题目链接：150. 逆波兰表达式求值 - 力扣（LeetCode）

文章讲解：代码随想录

视频讲解：栈的最后表演！ | LeetCode：150. 逆波兰表达式求值_哔哩哔哩_bilibili

题目建议：本题不难，但第一次做的话，会很难想到，所以先看视频，了解思路再去做题

class Solution {
    public int evalRPN(String[] tokens) {
        
    }
}

题目解析

1. 栈与递归的关系

核心观点：递归的本质可以用栈来实现，因为递归调用的过程就是函数不断入栈和出栈的过程。
示例：二叉树的前序/中序/后序遍历，既可以用递归实现（隐式栈），也可以用栈手动模拟（显式栈）。
关键结论：栈和递归可以相互转换，递归的深层调用栈就是栈结构的一种应用。

2. 逆波兰表达式（后缀表达式）与二叉树后序遍历

核心观点：逆波兰表达式是二叉树后序遍历的结果。
- 运算符是中间节点，操作数是叶子节点。
- 例如：3 4 + 5 × 对应的二叉树：
```
    ×
   / \
  +   5
 / \
3  4
```
- 后序遍历（左右根）的结果就是逆波兰表达式。
关键结论：理解逆波兰表达式有助于理解二叉树的后序序列化，但解题时无需显式构建二叉树。

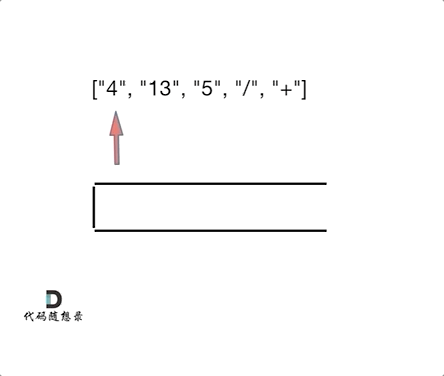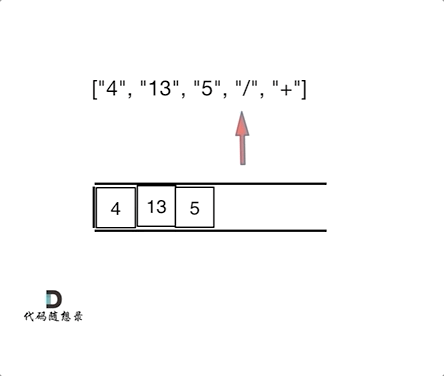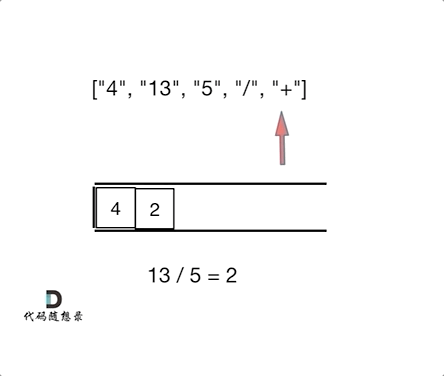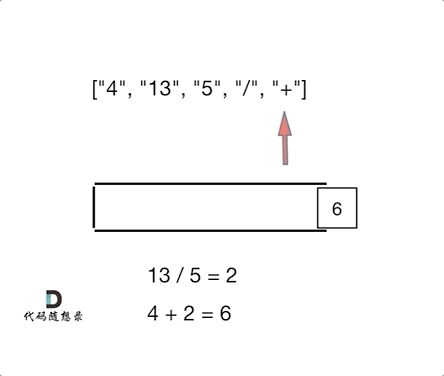
3. 逆波兰表达式求值 vs. 相邻字符消除（对对碰）

相似点：
- 相邻运算：逆波兰表达式每次遇到运算符，就计算最近的两个操作数，类似于1047.删除相邻重复项的“对对碰”逻辑。
- 栈的应用：两者都依赖栈结构处理相邻元素：
  - 逆波兰表达式：遇到数字入栈，遇到运算符弹出栈顶两个数计算，结果再入栈。
  - 删除相邻重复项：遇到相同字符就弹出栈顶，否则入栈。
区别：
- 逆波兰表达式：计算相邻操作数，生成新结果。
- 删除相邻重复项：匹配相邻相同字符，直接删除。

4. 总结

栈 ≈ 递归：递归调用本质是栈操作，两者可互相转换（如二叉树遍历）。
逆波兰表达式 = 二叉树后序遍历：运算符是中间节点，但解题时无需显式建树。
核心操作 = 栈 + 相邻计算：
- 逆波兰表达式：数字入栈，遇运算符计算栈顶两数，结果回栈。
- 类似题目：1047.删除相邻重复项，但匹配逻辑不同（计算 vs. 删除）。

一句话概括：逆波兰表达式求值是通过栈模拟后序遍历的“计算版对对碰”，核心是栈处理相邻元素的思想。

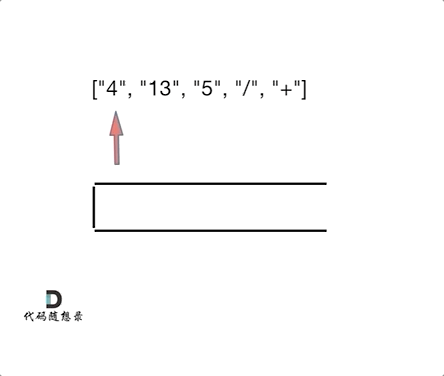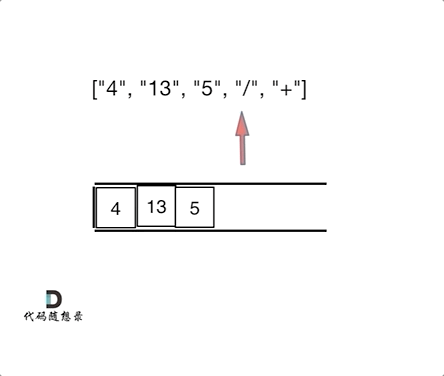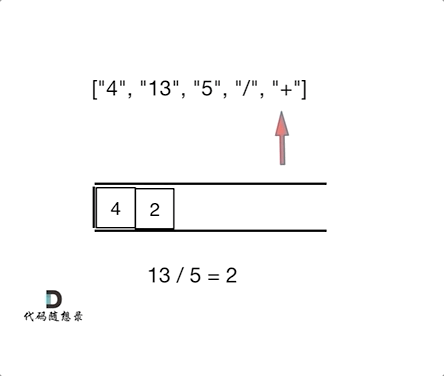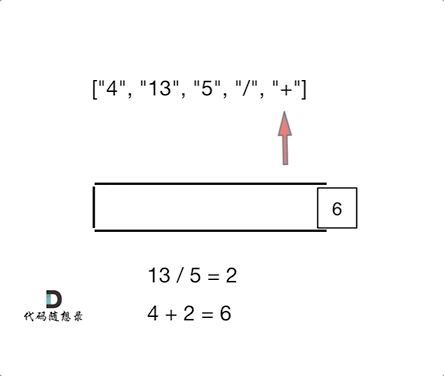
完整代码

滑动窗口最大值

题目链接：239. 滑动窗口最大值 - 力扣（LeetCode）

文章讲解：代码随想录

视频讲解：单调队列正式登场！| LeetCode：239. 滑动窗口最大值_哔哩哔哩_bilibili

题目建议：

有点难度，可能代码写不出来，但一刷至少需要理解思路
之前讲的都是栈的应用，这次该是队列的应用了。本题算比较有难度的，需要自己去构造单调队列，建议先看视频来理解。

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        
    }
}

题目解析

问题分析

题目要求求解滑动窗口中的最大值。

暴力解法: 更新窗口后重新遍历一次窗口，时间复杂度为O(n × k)，效率较低。

优先级队列（大顶堆）无法有效处理窗口移动时的元素移除问题。

因此，使用单调队列是更优的解决方案。

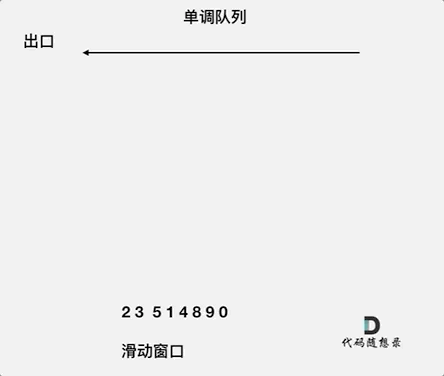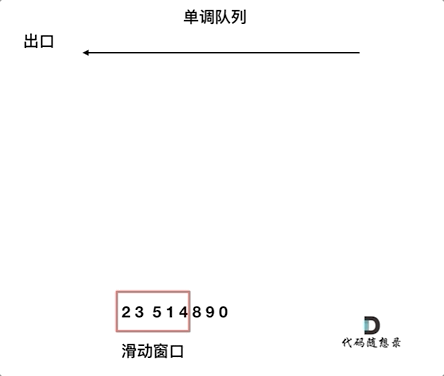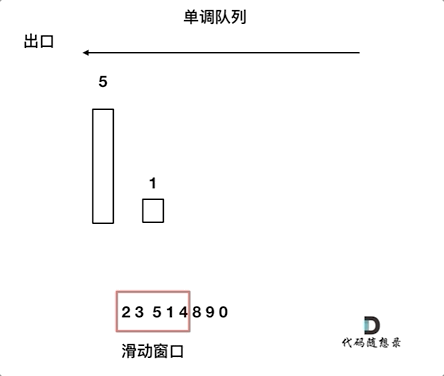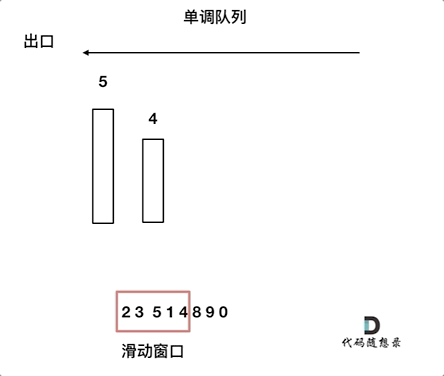
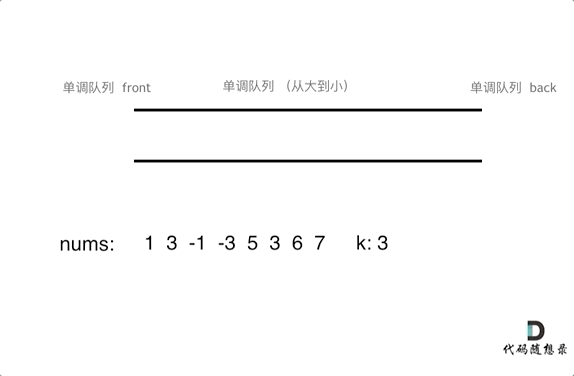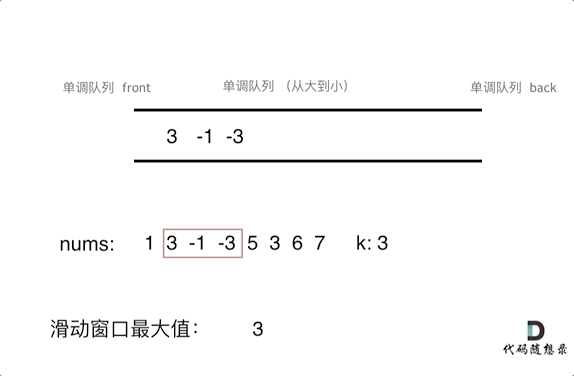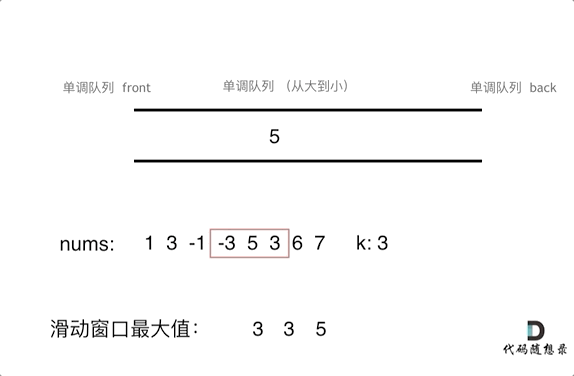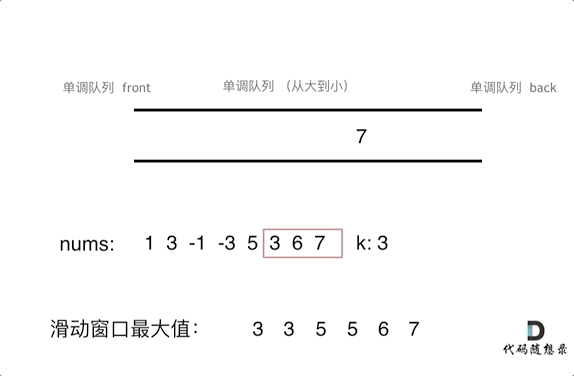
单调队列设计

单调队列是一种特殊的队列，队列中的元素按照某种单调性（如单调递减或单调递增）排列。

本题中，单调队列需要满足以下规则：

add(value)：在将元素加入队列之前，先将队列内所有小于该元素的值弹出，以保持队列单调递减。
poll(value)：如果窗口移除的元素等于队列出口元素，则弹出队列出口元素。
peek()：队列出口元素即为当前窗口的最大值。

数据结构选择

使用Deque（双端队列）实现单调队列，因为它支持在两端进行高效的插入和删除操作：

完整代码

方法一：直接使用 Deque

方法二：模拟符合题目解析的 Queue

使用Deque实现单调队列，保持队列单调递减。
每次窗口移动时，通过pop和push操作维护单调队列。
队列出口元素始终是当前窗口的最大值。
时间复杂度为O(n)，空间复杂度为O(k)。

前 K 个高频元素

题目链接：347. 前 K 个高频元素 - 力扣（LeetCode）

文章讲解：代码随想录

视频讲解：优先级队列正式登场！大顶堆、小顶堆该怎么用？| LeetCode：347.前 K 个高频元素

题目建议：

大/小顶堆的应用，在C++中就是优先级队列
有点难度，可能代码写不出来，一刷至少需要理解思路
本题是大数据中取前k值的经典思路，了解想法之后，不算难。

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        
    }
}

题目解析

因为题目中说：设计算法的时间复杂度必须优于 O(n log n) ，其中 n 是数组大小

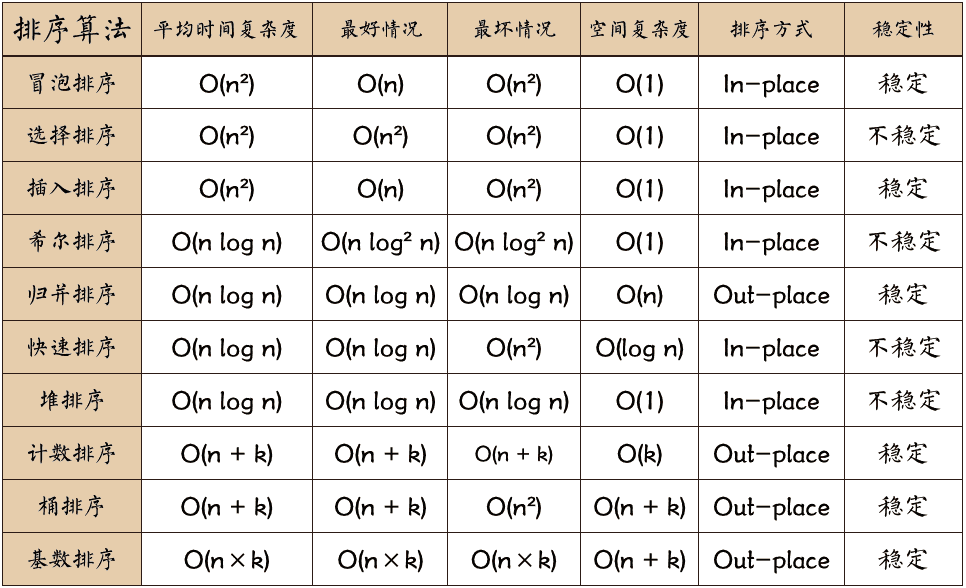
可以发现，使用常规的诸如冒泡、选择、甚至快速排序都是不满足题目要求，它们的时间复杂度都是大于或者等于 O(nlog⁡n)，而题目要求算法的时间复杂度必须优于 O(nlogn)。

对于 Top-K 问题，我们需要找到出现次数最高的前 K 个元素。通过创建小根堆（PriorityQueue），可以高效地解决这一问题：

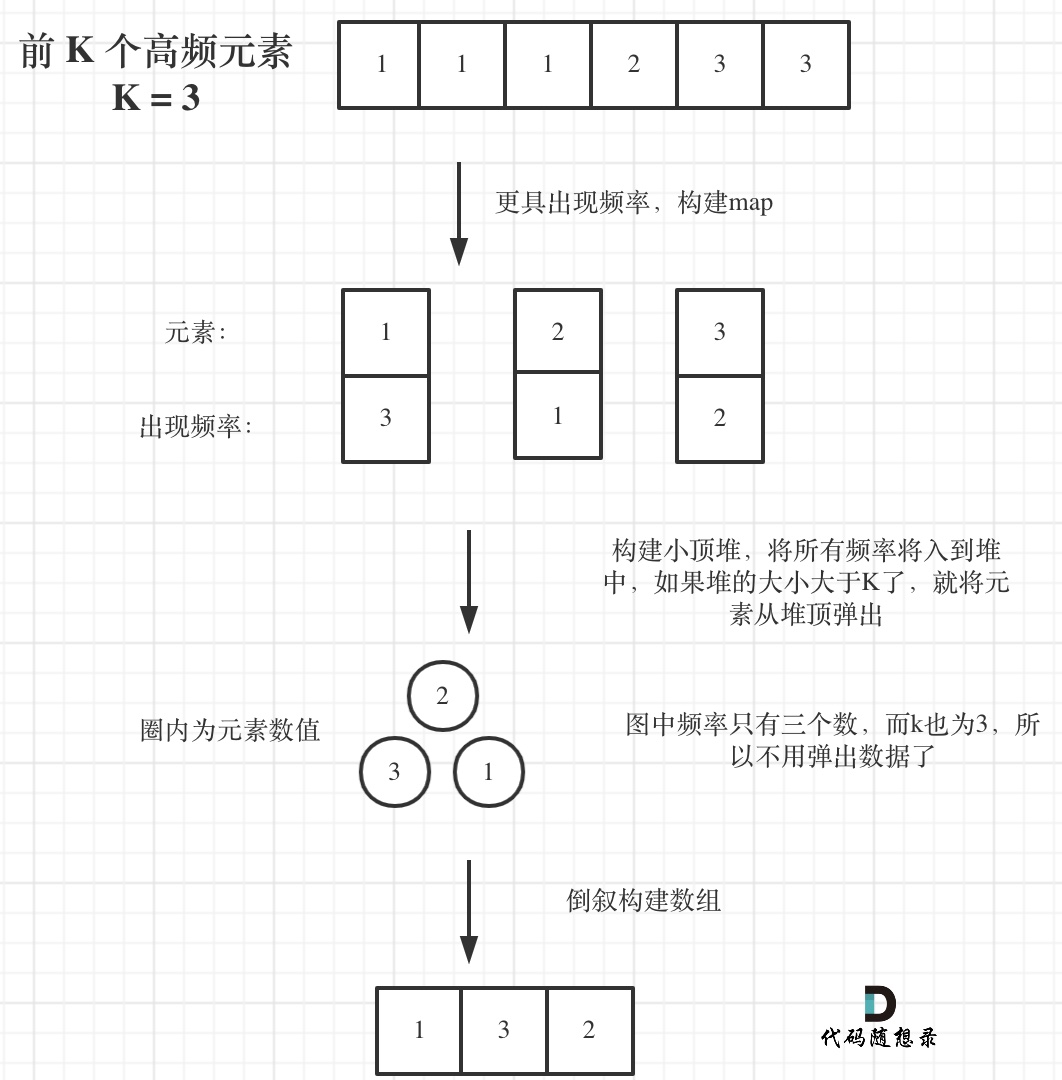
具体步骤：

借助哈希表来建立数字和其出现次数的映射，遍历一遍数组统计元素的频率；
维护一个元素数目为 k 的最小堆；
每次都将新的元素与堆顶元素（堆中频率最小的元素）进行比较；
如果新的元素的频率比堆顶端的元素大，则弹出堆顶端的元素，将新的元素添加进堆中；
最终，堆中的 k 个元素即为前 k 个高频元素；

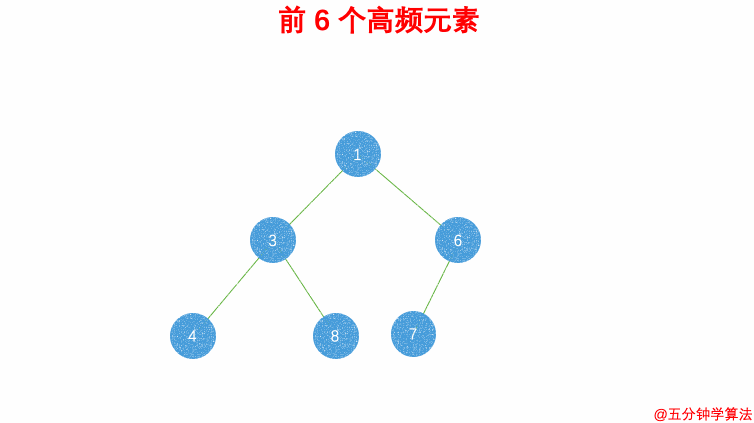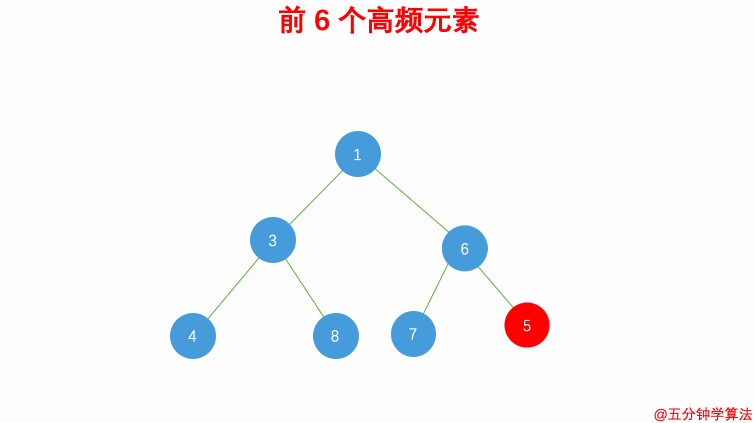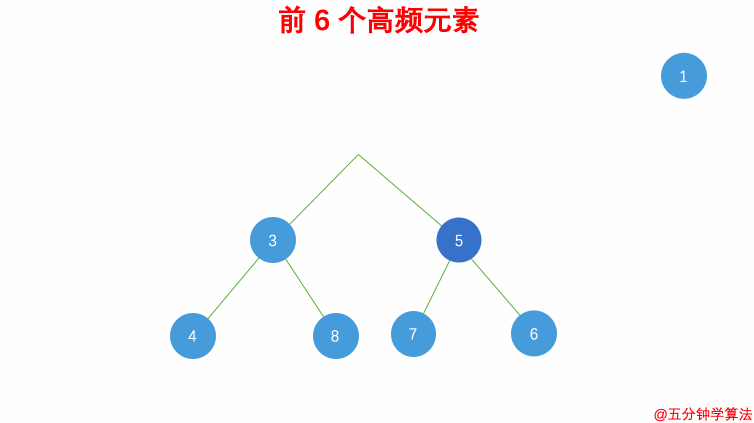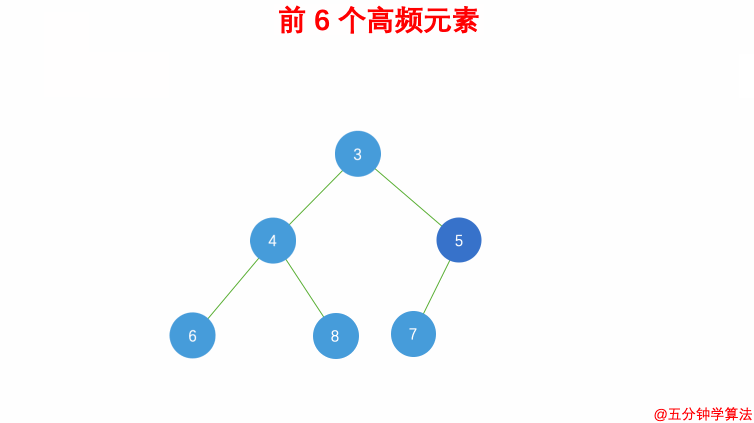
完整代码

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>();

        for (int n : nums) {
            map.put(n, map.getOrDefault(n, 0) + 1);
        }

        PriorityQueue<Map.Entry<Integer, Integer>> minHeap = new PriorityQueue<>(
                new Comparator<Map.Entry<Integer, Integer>>() {
                    @Override
                    public int compare(Map.Entry<Integer, Integer> o1, Map.Entry<Integer, Integer> o2) {
                        return o1.getValue().compareTo(o2.getValue());
                    }
                });

        for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
            if (minHeap.size() < k) {
                minHeap.add(entry);
            } else {
                Map.Entry<Integer, Integer> top = minHeap.peek();
                if (top.getValue().compareTo(entry.getValue()) < 0) { // err: 对象的比较不能用 <
                    minHeap.poll();
                    minHeap.add(entry);
                }
            }
        }
        int[] ret = new int[k];
        for (int i = k - 1; i >= 0; i--) {
            ret[i] = minHeap.poll().getKey(); // err: 不是 getValue()
        }

        return ret;
    }
}

前 K 个高频单词

题目链接：692. 前K个高频单词 - 力扣（LeetCode）

class Solution {
    public List<String> topKFrequent(String[] words, int k) {
        
    }
}

题目解析

所以我们需要对比较规则进行进一步细分；

完整代码

class Solution {
    public List<String> topKFrequent(String[] words, int k) {
        Map<String, Integer> map = new HashMap<>();

        for (String word : words) {
            map.put(word, map.getOrDefault(word, 0) + 1);
        }

        PriorityQueue<Map.Entry<String, Integer>> minHeap = new PriorityQueue<>(
                new Comparator<Map.Entry<String, Integer>>() {
                    @Override
                    public int compare(Map.Entry<String, Integer> o1, Map.Entry<String, Integer> o2) {
                        if (o1.getValue().compareTo(o2.getValue()) == 0) {  
                            // 关键err: value 同, 比较 key 的首字母随更小, key 小的优先
                            return o2.getKey().compareTo(o1.getKey()); 
                        }
                        return o1.getValue().compareTo(o2.getValue());
                    }
                });

        for (Map.Entry<String, Integer> word : map.entrySet()) {
            // err: 遍历的不是 String[] words, 而是 map.entrySet()
            if (minHeap.size() < k) {
                minHeap.add(word);
            } else {
                Map.Entry<String, Integer> top = minHeap.peek();
                int tmp = top.getValue().compareTo(word.getValue());
                if (tmp == 0) {
                    if (top.getKey().compareTo(word.getKey()) > 0) {
                        // 关键err: value 同, 比较 key 的首字母随更小, key 小的优先
                        minHeap.poll();
                        minHeap.add(word);
                    }
                } else if (tmp < 0) {
                    minHeap.poll();
                    minHeap.add(word);
                }
            }
        }

        String[] ret = new String[k];
        
        for (int i = k - 1; i >= 0; i--) {
            ret[i] = minHeap.poll().getKey();
        }
        
        return Arrays.asList(ret);  // err: 注意返回值是 List<String>, 不是数组
    }
}

补充知识

Stack API

Java 提供了 java.util.Stack 类来实现栈的功能。栈是一种后进先出（LIFO）的数据结构。

常用方法：

push(E item)
- 功能：将一个元素压入栈顶。
- 示例：stack.push("Hello");

pop()
- 功能：移除并返回栈顶元素。如果栈为空，会抛出 EmptyStackException。
- 示例：String top = stack.pop();

peek()
- 功能：返回栈顶元素，但不移除它。如果栈为空，会抛出 EmptyStackException。
- 示例：String top = stack.peek();

isEmpty()
- 功能：判断栈是否为空。
- 示例：boolean empty = stack.isEmpty();

size()
- 功能：返回栈中元素的数量。
- 示例：int size = stack.size();

search(Object element)
- 功能：从栈顶开始查找元素的位置（从1开始计数）。如果未找到，返回 -1。
- 示例：int position = stack.search("Hello");

import java.util.Stack;

public class StackExample {
    public static void main(String[] args) {
        Stack<String> stack = new Stack<>();
        stack.push("A");
        stack.push("B");
        stack.push("C");

        System.out.println("Top element: " + stack.peek()); // 输出 C
        System.out.println("Popped element: " + stack.pop()); // 输出 C
        System.out.println("Size: " + stack.size()); // 输出 2
    }
}

Queue API

Java 提供了 java.util.Queue 接口，以及其实现类（如 LinkedList、ArrayDeque 等）来实现队列的功能。队列是一种先进先出（FIFO）的数据结构。

常用方法：

add(E e)
- 功能：将一个元素插入队列的尾部。如果队列已满（对于有容量限制的队列），会抛出 IllegalStateException。
- 示例：queue.add("Hello");

offer(E e)
- 功能：将一个元素插入队列的尾部。如果插入成功返回 true，如果队列已满返回 false。
- 示例：boolean added = queue.offer("Hello");

remove()
- 功能：移除并返回队列头部的元素。如果队列为空，会抛出 NoSuchElementException。
- 示例：String head = queue.remove();

poll()
- 功能：移除并返回队列头部的元素。如果队列为空，返回 null。
- 示例：String head = queue.poll();

element()
- 功能：返回队列头部的元素，但不移除它。如果队列为空，会抛出 NoSuchElementException。
- 示例：String head = queue.element();

peek()
- 功能：返回队列头部的元素，但不移除它。如果队列为空，返回 null。
- 示例：String head = queue.peek();

isEmpty()
- 功能：判断队列是否为空。
- 示例：boolean empty = queue.isEmpty();

size()
- 功能：返回队列中元素的数量。
- 示例：int size = queue.size();

import java.util.LinkedList;
import java.util.Queue;

public class QueueExample {
    public static void main(String[] args) {
        Queue<String> queue = new LinkedList<>();
        queue.add("A");
        queue.add("B");
        queue.add("C");

        System.out.println("Head element: " + queue.peek()); // 输出 A
        System.out.println("Removed element: " + queue.poll()); // 输出 A
        System.out.println("Size: " + queue.size()); // 输出 2
    }
}