408 17——42题

题目：

使用Prim(普里姆)算法求带权连通图的最小(代价)生成树(MST)。请回答下列问题。
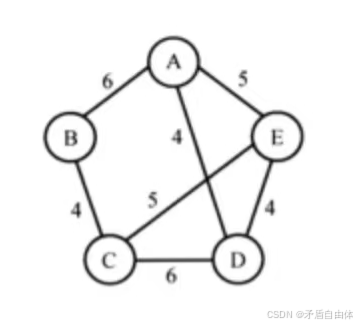
(1)对下列图G，从顶点A开始求G的MST，依次给出按算法选出的边。
(2)图G的MST是唯一的吗?

 

 (3)对任意的带权连通图，满足什么条件时，其MST是唯一的?

答案：

1. 从顶点A开始，按Prim算法求出最小生成树的边

Prim算法步骤：

1. 从顶点A开始，将A加入到生成树中，选择连接A的最小权重的边。可选的边是：A-B（6），A-E（5），最小的是A-E（5），所以选择边A-E。

2. 已加入生成树的顶点为**{A, E}。从已加入生成树的顶点开始，选择连接E或A的其他顶点的最小边。可选边为：A-B（6），A-C（4），E-D（6），E-C（5），最小的是A-C（4）**，所以选择边A-C。

3. 已加入生成树的顶点为**{A, E, C}。接下来可选的边为：A-B（6），E-D（6），C-D（4），最小的是C-D（4）**，所以选择边C-D。

4. 已加入生成树的顶点为**{A, E, C, D}。剩余的可选边为：A-B（6），E-D（6），最小的是A-B（6）**，所以选择边A-B。

5. 最后，所有顶点都已加入生成树，最小生成树完成。

最小生成树的边：

• A-E（5）
• A-C（4）
• C-D（4）
• A-B（6）

2. 图G的MST是唯一的吗？

最小生成树是否唯一，取决于图中是否存在等权重的边。如果图中有多条等权重的边，那么可能会存在多个不同的生成树。

在这个图中，虽然有两条边的权重都是4（C-D和A-C），但是Prim算法按照特定的顺序选择最小边，因此根据我们选取的边顺序，生成的MST是唯一的。

3. 对于任意的带权连通图，满足什么条件时，MST是唯一的？

对于任意带权连通图，最小生成树唯一的条件是所有边的权重都不同。这是因为如果边的权重相同，可能存在多条不同的边可以组成相同权重的最小生成树，因此MST可能不唯一。

 

知识点：

1. 最小生成树（Minimum Spanning Tree，MST）

• 定义：最小生成树是一个无向加权图的子图，它包含图中所有的顶点，并且这些顶点之间的边的权重和最小，且没有回路。
• 应用场景：最小生成树广泛应用于网络设计问题，如设计最经济的电网、通信网络或道路系统等。在实际问题中，MST用于寻找最低成本的连接方案。

2. Prim算法

• Prim算法是一种用于求解最小生成树的贪心算法，它通过逐步扩展已构建的树来找到整个图的最小生成树。
• 算法步骤：
  1. 从任意一个节点开始，将它作为生成树的起点。
  2. 每一步选择当前生成树中的节点与生成树外的节点之间权重最小的边，将该边和新节点加入到生成树中。
  3. 重复这个过程，直到所有节点都被加入到生成树中。
• 时间复杂度：若使用最小堆优化，时间复杂度为 O(Elog⁡V)O(E \log V)O(ElogV)，其中 EEE 是图的边数，VVV 是图的顶点数。

3. 贪心算法

• 定义：贪心算法是每一步都做出局部最优选择，期望通过这样的局部最优选择最终得到全局最优解。
• 在MST中的应用：Prim算法和Kruskal算法都是基于贪心思想，每次选择最小的边来扩展生成树。贪心策略确保了算法能够得到一个最小生成树。

4. 图的存储结构

• 邻接矩阵：图中的顶点和边可以用一个二维数组存储，数组中的元素表示顶点之间的边及其权重。这种方法适合稠密图，查询效率高，但空间复杂度为 O(V2)O(V^2)O(V2)，不适合边数较少的稀疏图。
• 邻接表：使用链表或者哈希表存储每个顶点相邻的边，适合稀疏图。空间复杂度为 O(V+E)O(V + E)O(V+E)，查询相对邻接矩阵慢一些，但节省了空间。

5. 边权重与唯一性

• 最小生成树的唯一性：如果图中的边权重都不同，则最小生成树是唯一的。否则，若图中存在多条权重相同的边，可能会存在多个不同的最小生成树。
• 在本题中，虽然边A-C和C-D的权重相同（都是4），但由于Prim算法每次选择权重最小的边且选择顺序固定，导致最小生成树是唯一的。

6. Kruskal算法

• Kruskal算法也是用于求解最小生成树的另一种常用算法。它的核心思想是按照边的权重从小到大排序，然后逐步将最小的边加入到生成树中，保证不会形成回路。
• 这种方法更适合处理稀疏图，因为它通过排序边来减少不必要的边的处理。

7. 图论中的其他概念

• 连通图：一个图中任意两个顶点之间都存在路径，则该图是连通图。最小生成树只存在于连通图中。
• 带权图：图中每条边都有一个数值（权重），通常表示两点之间的距离、费用或其他相关的度量。

8. 权重与网络设计问题

• 在网络设计中，边权重通常表示两节点之间的距离、成本或延迟，MST可以用于最小化整体连接成本。在实际的网络优化中，选择最小的权重有助于减少建设或维护成本。

9. 图论与其他算法

• Dijkstra算法：用于求解单源最短路径问题，与Prim算法的结构类似，但目的不同，Dijkstra是求从一个顶点到其他顶点的最短路径，而Prim算法是求最小生成树。
• Bellman-Ford算法：也是求解最短路径问题，能处理带负权边的图。