第二周分享内容

一定要说一下这个题

石头剪刀布（改）

题目描述

石头剪刀布是常见的猜拳游戏：石头胜剪刀，剪刀胜布，布胜石头。如果两个人出拳一样，则不分胜负。

如今出现了一种石头剪刀布的升级版游戏。升级版游戏在传统的石头剪刀布游戏的基础上，增加了两个新手势：石石头。剪剪刀。

这五种手势的胜负关系如表一所示，表中列出的是甲对乙的游戏结果。

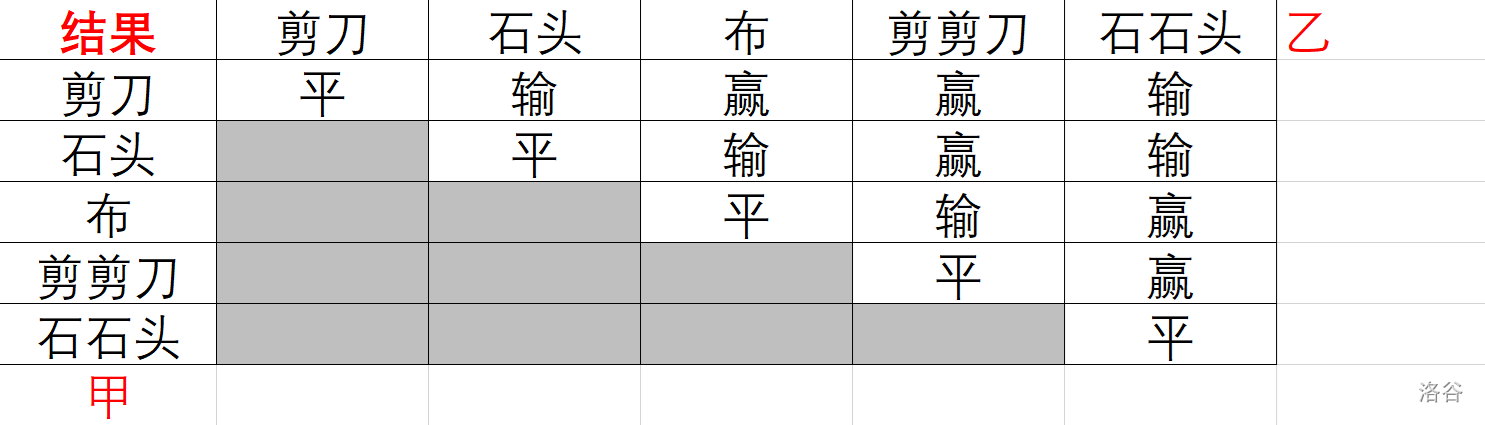
现在，小A和小B尝试玩这种升级版的猜拳游戏。已知他们的出拳都是有周期性规律的，但周期长度不一定相等。例如：如果小A以 石头-布-石头-剪刀-剪剪刀-石石头 长度为6的周期出拳，那么他的出拳序列就是石头-布-石头-剪刀-剪剪刀-石石头-石头-布-石头-剪刀-剪剪刀-石石头-…… ，而如果小B以剪刀-石头-布-石石头-剪剪刀 长度为 $5$ 的周期出拳，那么他出拳的序列就是 剪刀-石头-布-石石头-剪剪刀-剪刀-石头-布-石石头-剪剪刀-……。
已知小A和小B一共进行 $N$ 次猜拳。每一次赢的人得 $1$ 分，输的得 $0$ 分；平局两人都得 $0$ 分。现请你统计 $N$ 次猜拳结束之后两人的得分。

输入格式

第一行包含三个整数：$N,N_A,N_B$，分别表示共进行 $N$ 次猜拳、小 A 出拳的周期长度，小 B 出拳的周期长度。数与数之间以一个空格分隔。

第二行包含 $N_A$ 个整数,表示小 A 出拳的规律,第三行包含 $N_B$ 个整数，表示小 B 出拳的规律。其中，$0$ 表示 剪刀，$1$ 表示 石头，$2$ 表示 布，$3$ 表示 剪剪刀，$4$ 表示 石石头。数与数之间以一个空格分隔。

输出格式

输出一行，包含两个整数，以一个空格分隔，分别表示小 A、小 B 的得分。

样例 #1

样例输入 #1

10 5 6
0 1 2 3 4
0 3 4 2 1 0

样例输出 #1

6 2

提示

【数据范围】

对于 $20\%$ 的数据，$N,N_A,N_B=1$ 。

对于 $60\%$ 的数据，$0<N\le 200,0<N_A\le 200,0<N_B\le 200$ 。

对于 $100\%$ 的数据，$0<N\le 5\times 10^5,0<N_A\le 5\times 10^5,0<N_B\le 5\times 10^5$ 。

第一次写的很复杂，用了感觉有(无穷个if)，插入一点片段

	if(a[i]==2&&b[j]==0)
			{
				cntb++;
			}
			if(a[i]==0&&b[j]==3)
			{
				cnta++;
			}
			if(a[i]==3&&b[j]==0)
			{
				cntb++;
			}

后面听学长的方法非常奇妙 利用二维数组来表示输赢 1为赢-1为输0为平局 上代码

#include<bits/stdc++.h>

using namespace std;
const int N = 5e5;
int a[N],b[N];

int main()
{
	int q[5][5]={
	{0,-1,1,1,-1},
	{1,0,-1,1,-1},
	{-1,1,0,-1,1},
	{-1,-1,1,0,1},
	{1,1,-1,-1,0}
	};
    
    int n,na,nb;
    cin>>n>>na>>nb;
    int cnta=0,cntb=0;
    int i,j;
    int k = 0;
    int m = 0;
    for(i = 0;i<na;i++)
    {
    	cin>>a[i];
    }
	for(j = 0;j<nb;j++)
	{
		cin>>b[j];
	}
    while(n--)
    {
        
	    if(q[a[k]][b[m]]==1)
	    {
			cnta++;
		}
		if(q[a[k]][b[m]]==-1)
		{
			cntb++;
		}
	    k++,m++;
        if(k == na) k = 0 ;
        if(m == nb) m = 0;
        
	}
	cout<<cnta<<" "<<cntb;	
	return 0;
}

在while循环里遇到了很多问题，首先，k不会无限的加，达到周期以后要变为第一个数字，第二，对k++和m++的位置放置很重要 如果放在if前面就会从q[a[1]] [b[1]]开始了，这个问题没有注意到。

再分享一下高精度的模板 新学了高精度乘高精度的
1.高精度加法

#include<bits/stdc++.h>

using namespace std;

vector<int> Add(vector<int> &A ,vector<int> &B)
{
	vector<int> C;
	int t = 0;
	for(int i = 0;i<A.size() || i<B.size();i++)
	{
		if(i<A.size())
		{
			t+=A[i];
		}
		if(i<B.size())
		{
			t+=B[i];
		}
		C.push_back(t%10);
		t/=10;
	}
	if(t)
	{
		C.push_back(1);
	}
	return C;
}

int main()
{
	string a,b;
	vector<int> A;
	vector<int> B;
	cin>>a>>b;
	for(int i = a.size()-1;i>=0;i--)
	{
		A.push_back(a[i]-'0');
	}
	for(int i = b.size()-1;i>=0;i--)
	{
		B.push_back(b[i]-'0');
	}
	
	auto C = Add(A,B);
	
	for(int i = C.size()-1;i>=0;i--)
	{
		printf("%d",C[i]);
	}
	
	return 0;
}

高乘低

#include<bits/stdc++.h>

using namespace std;

vector<int> mul(vector<int> &A,int b)
{
	vector<int> C;
	int t = 0;
	for(int i = 0;i<A.size() || t;i++)
	{
		if(i<A.size())
		{
			t+=A[i]*b;
		}
		C.push_back(t%10);
		t/=10;
	}
	return C;
}

int main()
{
	string a;
	int b;
	
	vector<int> A;
	cin>>a>>b;
	for(int i = a.size()-1;i>=0;i--)
	{
		A.push_back(a[i]-'0');
	}
	
	auto C = mul(A,b);
	
	for(int i = C.size()-1;i>=0;i--)
	{
		cout<<C[i]; 
	}
	
	return 0;
}

高乘高

#include<bits/stdc++.h>

using namespace std;

const int N = 1e5+10;

int main()
{
    string a,b; 
    int A[N],B[N],C[N];
    cin>>a>>b;
    for(int i = 0;i<a.size();i++)
    {
        A[i]=a[a.size()-1-i]-'0';
    }
    for(int j = 0;j<b.size();j++)
    {
        B[j]=b[b.size()-1-j]-'0';
    }
    
    for(int i = 0;i<b.size();i++)
    {
        for(int j = 0;j<a.size();j++)
        {
            C[j+i]=C[j+i]+A[j]*B[i];
            if(C[j+i]>=10)
            {
                C[j+i+1]+=C[j+i]/10;
                C[j+i]=C[j+i]%10;
            }
        }
    }
    
    
    int ans = 0;
    int len = a.size()+b.size();
    for(int i = len-1;i>=0;i--)
    {
        if(C[i]!=0)
        {
            ans=i;
            break;
        }
    }
    for(int i = ans;i>=0;i--)
    {
        cout<<C[i];
    }
    return 0;
}