高中物理和大学物理中的脱离问题-CSDN博客

本文链接：https://blog.csdn.net/2402_87342010/article/details/148319260

一.引入惯性力的概念

为了方便高中生阅读本博客，我在这特地引入惯性力的相关概念。

1.什么是惯性力

由牛顿第二定律可知 $F=ma$ ①。即物体合力等于质量和加速度的乘积。

我们在①两边同时减去 $ma$ ——> $F-ma = 0$ ②。

我们令惯性力 $F_Q = -ma$ 。即惯性力大小等于ma，方向和加速度的方向相反。

则②式就变为 $F+F_Q=0$ 。即我们说我们在一个存在加速度的运动中加入一个方向相反，大小为 $ma$ 的惯性力。则此时受力平衡。

例1：质量为m的小球M用两根长均为l的无重细杆支承，如下图所示。小球与细杆一起以匀角速度 $\varpi$ 绕铅垂轴AB转动。设AB=l，求两杆所受的拉力。

解：对小球进行受力分析如下图

则 $X:F_{T1}*\cos30^{\circ}+F_{T2}*\cos30^{\circ} = F_Q$

$Y:F_{T1}*\sin30{^\circ}=F_{T2}*\sin30{^\circ}+mg$

$F_Q = ma = m\omega ^2*\sqrt3/2l$

联立上面三式得 $F_{T1}=mg+\frac{mw^2l}{2}$

$F_{T2}=-mg+\frac{mw^2l}{2}$

2.引入惯性力的意义

通过引入了惯性力，我们可以将有加速度的运动，即合力不为0的运动，改为合力为0的运动。

二.脱离问题的本质

我们知道若两个物品脱离，则说明两者之间恰好没有力。那么脱离问题的本质便是两个物体之间是否有相互作用力。若有相互作用力，则两者不脱离，否则两者脱离。或者我们说两物体的相互作用力有取值范围。

在一般的脱离问题中，一般是问你若使不脱离某个物理量最小或最大多少。

关于这种问题，我们来想一下为什么物理量会有取值范围——>最根本的原因是两个物体的相互作用力有取值范围(一般为单一方向，大小由0-正无穷)。这里我们说的比较抽象，我们在这不妨举一个例子。

在高中我们有学圆周运动，我们以重力场上的小球的圆周运动为例子，如下图所示

我们一般说这种圆周运动在最高点最容易脱离，但是我们高中并未对此现象进行细致的解释。在这我为次现象提供一个解释。供大家参考。

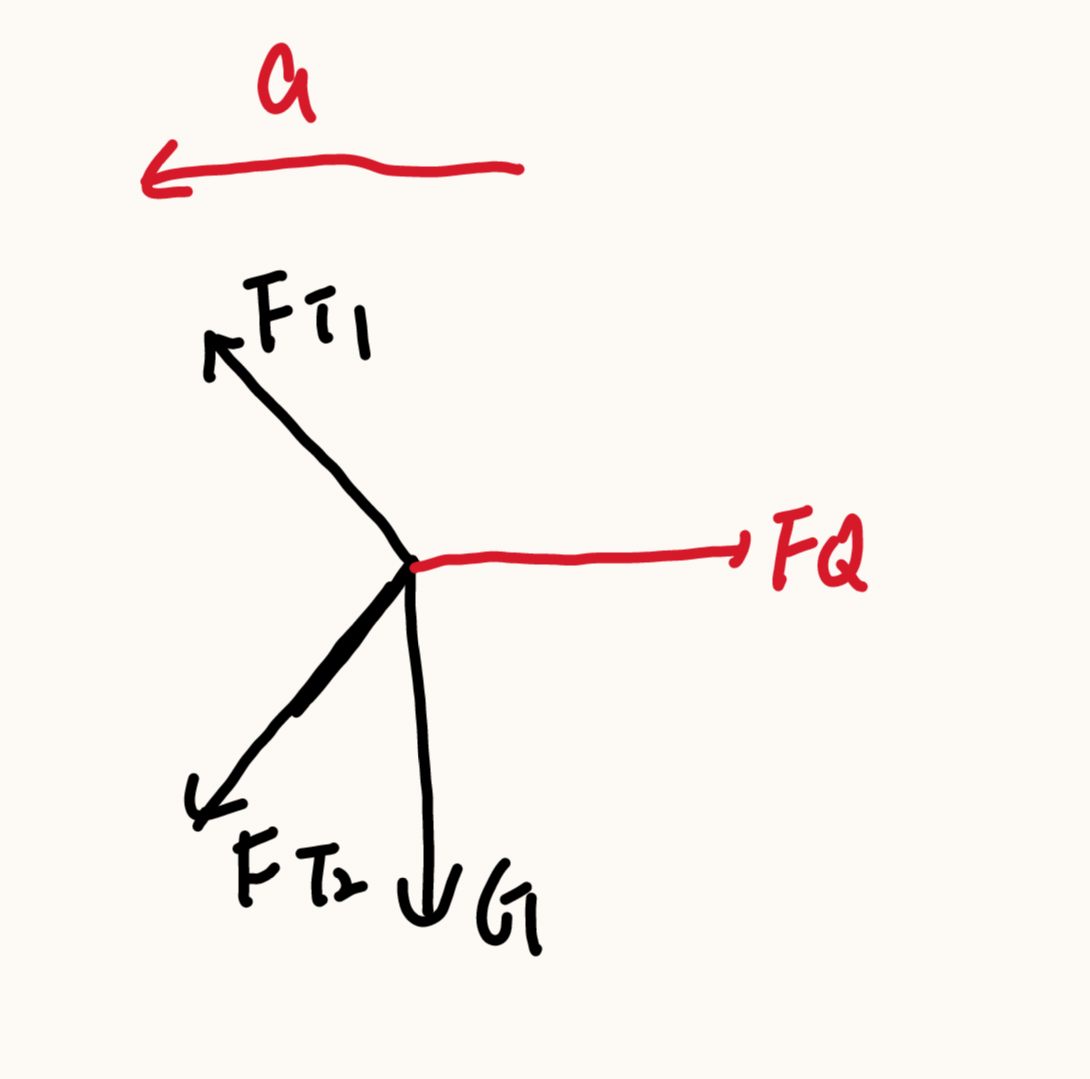
我们先对小球受力分析，小球受重量G，支持力N，方向均向下在高中我们说G和N提供了向心力，在这里我们用惯性力来理解。受力分析如下图

则 $F_Q = m*\frac{V^2}{R}= N+G$

我们知道在最高点轨道只会给予小球向下的支持力，则 $N\subset (0,+\infty )$

则 $F_Q\subset (mg,+\infty )$

$v\subset (\sqrt {gR}+\infty )$

所以若使得小球在轨道不脱离，即上面的惯性参考系下受力平衡， $v>\sqrt {gR}$

相反在最高点

此时受力分析如图

$F_Q = m*\frac{V^2}{R}= N-G$

明显 $v\subset (-\sqrt {gR}+\infty )$ 由于速度不可能为负值，故不会脱离

由上面的例子我可以明显的看出脱离问题的本质是相互作用力有取值范围——>相关物理量有取值范围。

如果题目的受力或者运动较为简单，那么我们只需直接假设两者之间恰好无相互作用力时即可。然后分析它是最大值还是最小值是不是就可以解了。

但是如果题目的受力或者运动较为复杂，或者有几个可能的最大值最小值点。如下面这道题所示

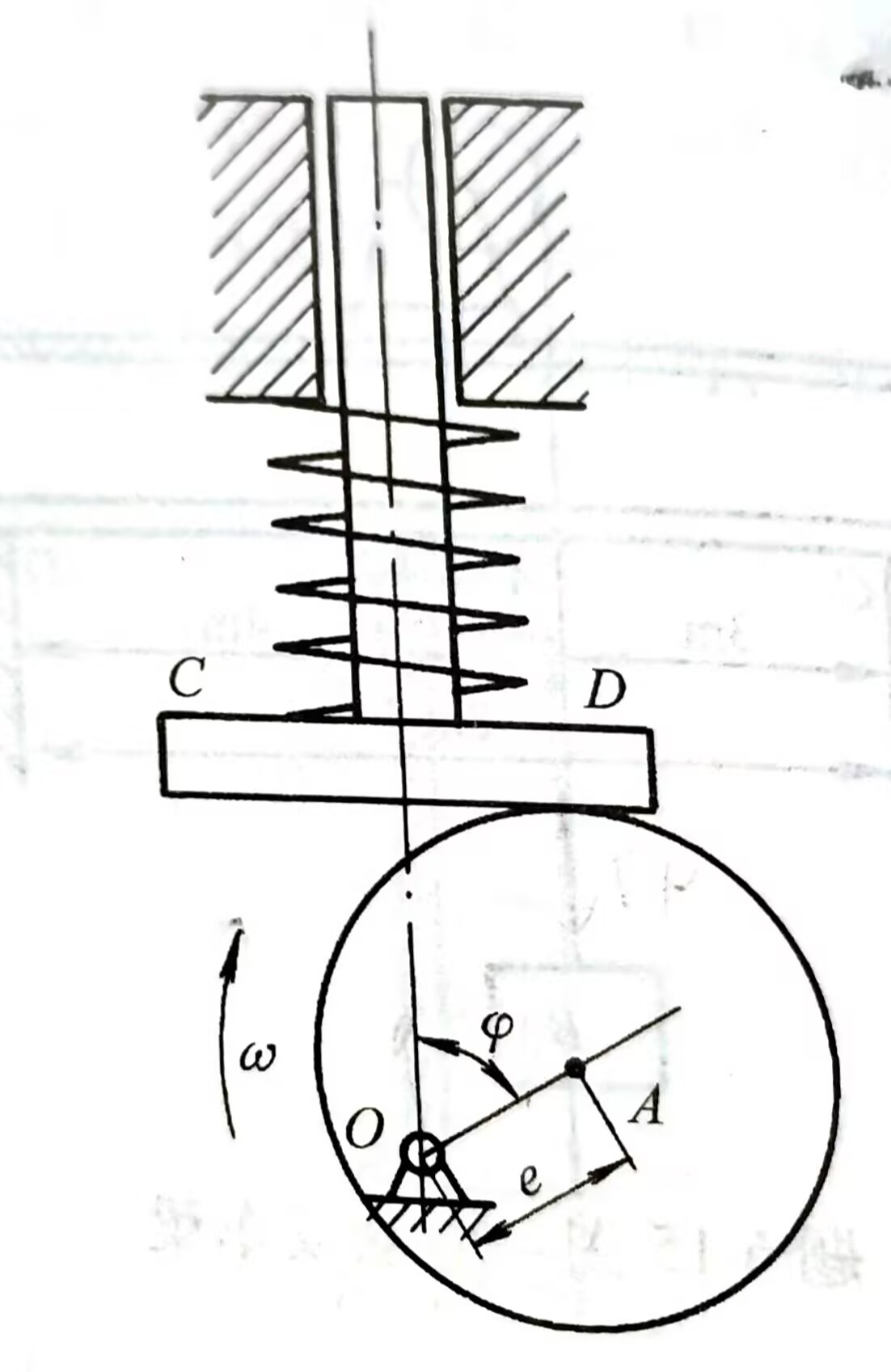
如图所示为凸轮导板机构，其偏心轮的偏心距 $OA=e$ ,偏心轮绕O轴以匀角速度 $w$ 转动。如当导板 CD在最低位置时，弹簧的压缩量为 $b$ ，导板质量为 $m$ ，试求弹簧的弹性系数 $k$ 为多大时，方使导板在运动过程始终与偏心轮保持接触。（本道题为大学的题目，各位见谅，短时间没找到类似的高中题目，找不到类似的典型题了）