反三角函数

小伙伴们，你们好！
相信大家和我一样，进入大学之后，发现数学很多知识点，老师一笔带过，但是我们却很懵的发现自己没学过。
这其中当属反三角函数。
下面我们一起进入反三角函数的学习吧!

反函数

学习反三角函数之前我们得先知道反函数的定义：
函数 y=f(x) 与其反函数 y=f ^-1(x) 的图像关于 y=x 直线对称。
例如：y=a^x (a>1) 与 y=log a^x 是反函数
以下是 a=2 时的图像

在这里我们浅浅了解一下反函数定义，下面我们进入反三角函数的学习。

反三角函数

1.y=arcsin x

学习 y=arcsin x 之前我们先复习一下 y=sin x的图像和性质，大家不要小瞧了原函数的性质，了解了原函数的性质才能更好的讨论反三角函数。

y=sin x

图像如下：

定义域 : R
值域 ：[-1,1]
奇函数
周期 ：2π

y = arcsin x

定义域 : [-1,1]
值域 ：R
奇函数
有界，无周期函数

注意：y = sin x，只有当 x ∈[-π/2，π/2] 时，才有 x = arcsin y，y∈[-1，1]。（x 可以表示弧度或角）

例如：

由此我们会得出两个小结论：
sin（arcsin a）= a , a ∈ [-1,1]
arcsin (sin a) = a , a ∈ [-π/2，π/2]

下面附上推论：

如果推论看不懂，我们可以试试带着上面的例题加以理解，小编再次上图：

相信大家的聪明才智，亲自上手试试，很快就可以掌握其中要领。

下面小编在贴上一张 y=arcsin x 和 y=sin x 一起的图像，方便大家记忆：

2.y=arccos x

y=cos x

图像如下：

定义域 : R
值域 ：[-1,1]
偶函数
周期 ：2π

y=arccos x

定义域 : [-1,1]
值域 ：[0,π]
非奇非偶
有界，无周期函数

同样的 y=arccos x 也有小结论：
1.cos（arccos x）= x ,x ∈ [-1,1]
arccos(cos x) = x ,x ∈ [0，π]

2.arccos (-x) = π - arccos x，x∈[-1,1]

3.arcsin x + arccos x = π/2 ，x∈[-1,1]

结论 1 的过程与 y=arcsin x 结论证明类似，有兴趣的小伙伴可以自己去试试，我下面给出结论二和三的证明：


如果理解不了，可以具体带数值，亲自动手试试哦。

以下附上y=cosx 和 y=arccosx函数的图像：

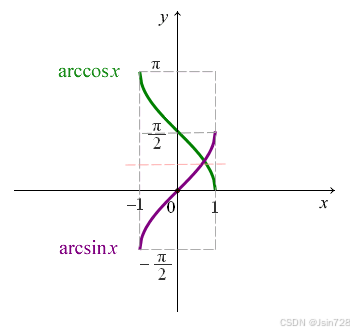
再来一张y=arcsin x 和y=arccos x函数的图像：

3.y=arctan x

y=tan x

定义域 :所有不是π/2+πk（k∈Z）的实数
值域 ：（+∞，-∞）
奇函数
周期：π

y= arctan x

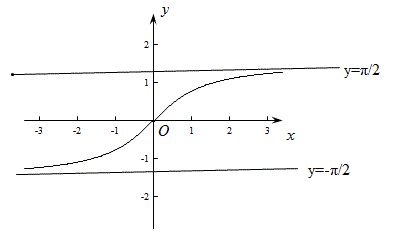
定义域 ：（+∞，-∞）
值域 ：（0，π）
奇函数
有界，无周期函数
这个极限后面会讲到的，不要着急，聪明的小伙伴可以直接在图上就能够看出来哦。

小结论：
tan(arctan x)=x , x∈R
arctan(tan x )=x , a∈（-π/2，π/2）

依旧是和上面类似的求法，我这里就不赘述了，希望大家还是可以亲自上手试试，加深记忆。

下面附上y=tan x和y=arctan x函数的图像：

希望大家可以好好学习这一章节，做好复习工作，一定要亲自动手去证明一下结论，以便加深记忆，那么我们下次再见！