Codeforces题解-CSDN博客

#include<iostream>
#include<vector>
using namespace std;
void solve()
{
    int n, m, k;
    cin >> n >> m >> k;
    vector<int> a(m);
    vector<int> b(k);
    vector<bool> used(n + 1, false);
    for (int i = 0; i < m; i++)
    {
        cin >> a[i];
    }
    for (int i = 0; i < k; i++)
    {
        cin >> b[i];
    }
    for (int i = 0; i < k; i++)
    {
        used[b[i]] = true;
    }
    int op = k;
    for (int i = 0; i < m; i++)
    {
        if (op == n || op == n - 1 && !used[a[i]])
        {
            cout << "1";
        }
        else {
            cout << "0";
        }
    }
    cout << endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t = 0;
    cin >> t;
    while (t--)
    {
        solve();
    }
}

这道是div3的C题1000分，思维还是相对比较简单的。

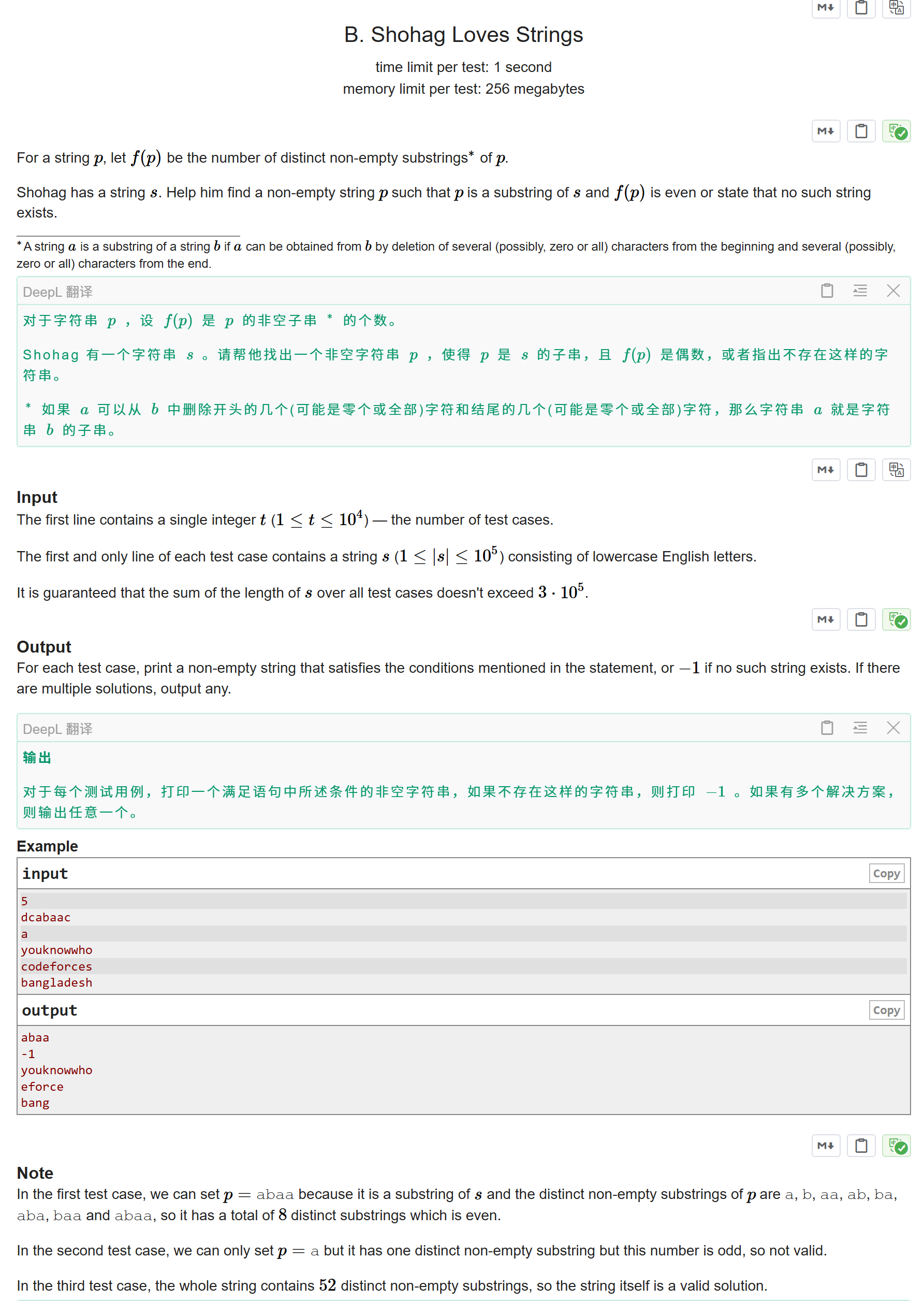
B. Shohag Loves Strings

这个是1000分关于字符串问题的

题目链接：Problem - 2039B - Codeforces

我的这个插件翻译可能不太准确，可以的话最好跳转题目链接。

题意分析：

我们有一个字符串 s，要找一个它的非空子串 p，使得 f(p) 为偶数。

其中 f(p) 定义为 p 的非空子串的个数。

题意还是比较简单的，思路我们需要分情况进行讨论。

算法思路：

若 p 的长度为 m，那么它的所有非空子串个数为：f(p)=（m*(m+1)）/2,这是求非空子串的公式，因为要求f(p)为偶数，并且只需要输出任意一个解决方案，那这个问题我们就可以特殊化一下。

1.先找长度为 2 且两个字符相同的子串

一般的，当长度 m=2 时，f(p)=3 是奇数，不满足条件，但当两个字符相等时，比如：aa, f(p)==2（满足条件）

所以这种情况就是相邻相同字符，如果没有这样的相邻相同字符，就找长度为 3 且三个字符互不相同的子串

长度 m=3时，f(p)=6（偶数）✅

如果上述两种情况都不存在，输出 -1。

源码实现：

#include<iostream>
#include<vector>
#include<string>
using namespace std;
void solve() {
    string s;
    cin >> s;
   
    for (int i = 0; i + 1 < s.length(); i++) {
        if (s[i] == s[i + 1]) {
            cout << s[i] << s[i + 1] << endl;
            return;
        }
    }

    for (int i = 0; i + 2 < s.length(); i++) {
        if (s[i] != s[i + 1] && s[i] != s[i + 2] && s[i + 1] != s[i + 2]) {
            cout << s.substr(i, 3) << endl;
            return;
        }
    }

    
    cout << -1 << endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t = 0;
    cin >> t;
    while (t--)
    {
        solve();
    }
}

特殊化处理还是比较简单的，我们需要注意的是aa这种情况。

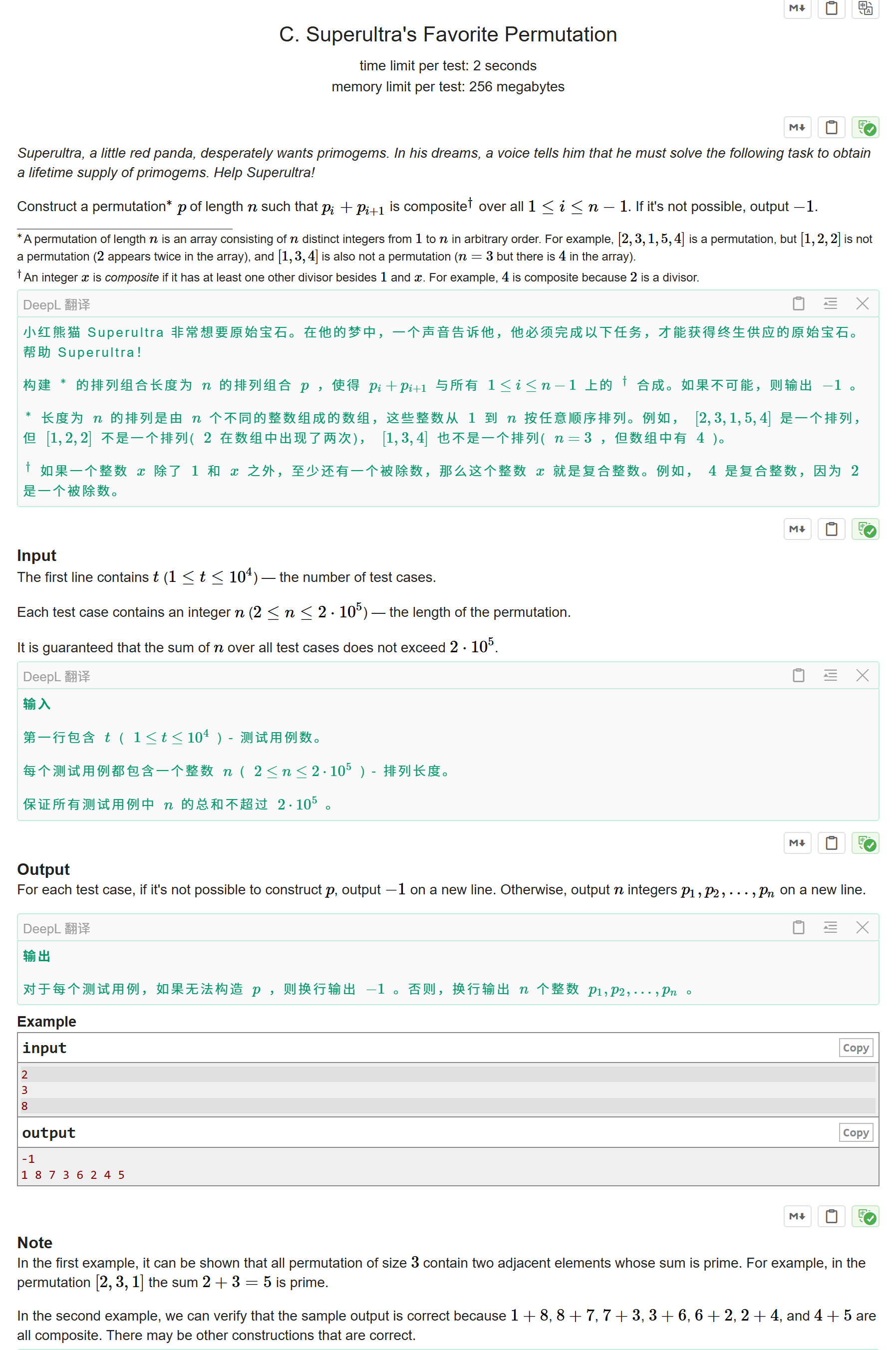
C. Superultra's Favorite Permutation

题目链接：Problem - 2037C - Codeforces

这是一道1000分的数学思维题，不难，需要多观察一下。

题意分析：

我们需要构造一个长度为 n 的排列 p，使得对于任意相邻两项 pi+pi+1 都是合数

合数：大于 1 的非质数，即除了 1 和它本身之外还有其他因数。

算法思路：

由数学推论可知：所有大于 2 的偶数都是合数，并且任何两个奇偶性相同的数相加起来都是合数。现在我们就只需要找到一个奇数和一个偶数相加为一个合数，这样我们就可以将这两个数作为连接奇数和偶数的桥梁，我们可以验证发现n≤4 中是没有这样的一对数，但是在 n=5 中存在 (4,5) ，它的和为 9 是一个合数。所以我们可以将奇数除了5之外都输出然后输出 5 4，再将偶数全部输出。

源码实现：

#include<iostream>
#include<vector>
#include<string>
using namespace std;
void solve() {
    int n;
    cin >> n;
    if (n < 5)
    {
        cout << -1 << endl;
        return;
    }
    for (int i = 1; i<= n; i+=2)
    {
       if(i!=5)
        cout << i << " ";
    }
    cout << "5 " << "4 " ;
    for (int i = 2; i <= n; i += 2)
    {
        
        if(i!=4)
            cout << i << " ";
    }
    cout << endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t = 0;
    cin >> t;
    while (t--)
    {
        solve();
    }
}

这道题还是很简单的数学思维。