数据结构-树、二叉树，森林，及其转换-CSDN博客

树（Tree）是 n(n >= 0) 个结点的有限集
- 若 n = 0 为空树
- 若 n > 0
  - 有且仅有一个特定的，称为根（Root）的结点
  - 其余结点可分为 m(m >= 0) 个互不相交的有限集T₁，T₂，...，Tₙ，其中每一个集合本身又是一棵树，称为根的子树（SubTree）

结点分类

根结点

非空树中无前驱结点的结点

结点的度（De-gree）

结点拥有的子树的个数
度为0的结点称为叶结点（Leaf）或终端结点
度不为0的结点称为非终端结点或分支结点
- 除了根结点之外，分支结点又称为内部结点

树的度

树内各结点的的度的最大值

结点间关系

孩子（Child）、双亲（Parent）

结点的子树的根称为该结点的「孩子」（Child）
D为B的「孩子」
该结点称为「孩子」的「双亲」（Parent）
B为D的「双亲」

兄弟（Sibing）、堂兄弟（Cousins）

同一个「双亲」的「孩子」之间互称为「兄弟」（Sibling）
B和C互为「兄弟」
「双亲」在同一层的结点互称为「堂兄弟」
D和E互为「堂兄弟」

祖先（ancestor)、子孙（descendant）

结点的「祖先」（ancestor）：从根到该结点所经分支上的所有结点
A、C 都是 F 的「祖先」（Ancestor）
F 是所有这些结点的「子孙」（Descendant）

结点的层次（Level）、树的深度（Depth）

结点的层次从根开始定义，根为第一层，根的「孩子」为第二层
- 若某结点在第 n 层，则其子树就在第 n + 1 层
树中结点的最大层次称为树的深度或树的高度

有序树、无序树、森林（Forest）

有序树：树中结点的各子树从左至右有次序
无序树：树中结点的各子树无次序
森林（Forest）：是 m(m >= 0）棵互不相交的树的集合

只有一棵树，是森林

有两棵树，是森林

总结

一棵树可以看成是一个特殊的森林
给森林中的各子树加上一个「双亲」结点，森林就变成了树

线性结构和树结构的差异

线性结构树结构
第一个数据元素：无前驱根结点（只有一个）：无双亲
最后一个数据元素：无后继叶结点（可以多个）：无孩子
中间元素：一个前驱、一个后继中间结点：一个双亲、多个孩子
一对一 一对多

树的存储结构

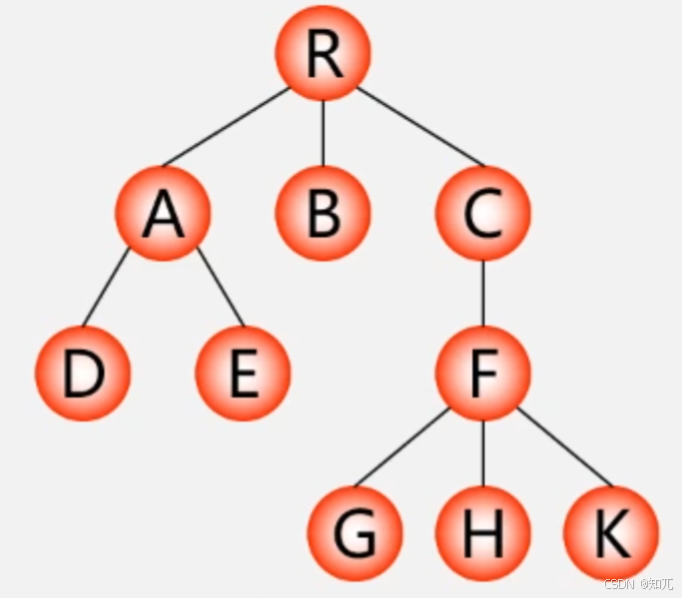
双亲表示法

假设以一组连续空间存储树的结点，同时在每个结点中，附设一个指示器指向双亲结点在数组中的位置。data是数据域，parent是指针域，存储该结点的双亲在数组中的下标（根结点为-1）
- 数据域：存放结点本身信息
- 双亲域：指示本结点的双亲结点在数组中的位置
- 为了存储方便，还要存储两个值，r 表示当前根结点的下标和 n表示当前结点个数
特点：找双亲容易，找孩子要遍历整个结构

R的双亲域为-1即，根结点
A、B、C 的的双亲域为0，即，它们三个的双亲都是 R
D、E 的双亲域为1，即，它们两个的双亲都是 A
以此类推

实现

typedef int TElemType;				/* 树结点的数据类型，目前暂定为整型 */

typedef struct PTNode				/* 结点结构 */
{
	TElemType data;					/* 结点数据域 */
	int parent;						/* 双亲位置域 */
} PTNode;

typedef struct						/* 树结构 */
{
	PTNode nodes[MAX_TREE_SIZE];	/* 结点数组 */
	int r, n;						/* 根的位置和结点数 */
} PTree;

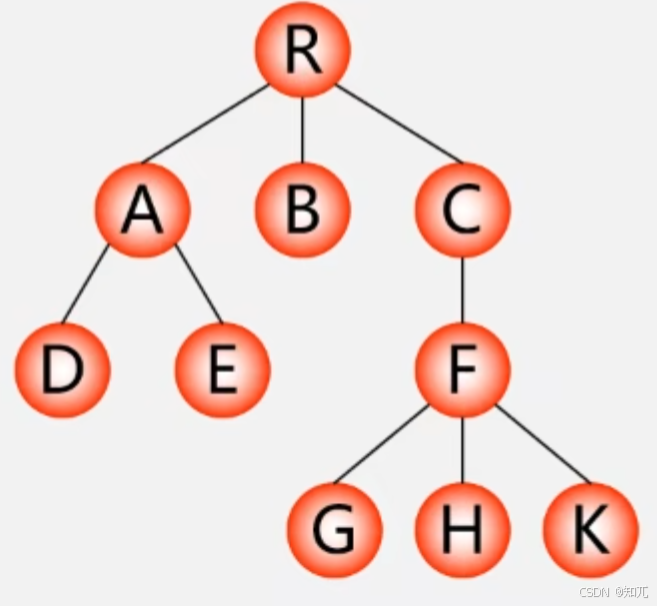
孩子表示法（孩子链表）

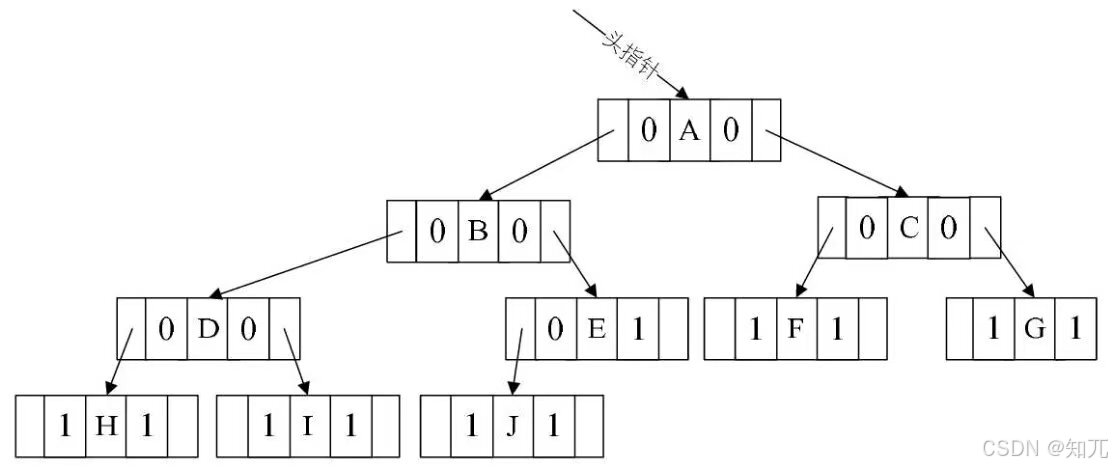
把每个结点的孩子结点排列起来，看成一个线性表，用单链表存储，则 n 个结点有 n 个孩子链表（叶子的孩子链表为空表）
n 个头指针又组成一个线性表，用顺序表（含 n 个元素的结构数组）存储
特点：找孩子容易，找双亲难

A 的孩子下标分别为3、5，所以 A 的孩子是 D 和 E
以此类推

实现

/* 树的孩子表示法结构定义 */
#define MAX_TREE_SIZE 100

typedef int TElemType;			/* 树结点的数据类型，目前暂定为整型 */

/* 孩子结点结构 */
typedef struct CTNode			
{
	int child;
	struct CTNode* next;
} *ChildPtr;

/* 双亲结点结构 */
typedef struct 					
{
	TElemType data;
	ChildPtr firstchild;  // 指向孩子的指针
} CTBox;

/* 树结构 */
typedef struct	     			
{
	CTBox nodes[MAX_TREE_SIZE];	/* 结点数组 */
	int r, n;					/* 根的位置和结点数 */
} CTree;

孩子兄弟表示法

任意一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右兄弟如果存在也是惟一的。
- 因此，我们可以设置两个指针，分别指向该结点的第一个孩子和此结点的右兄弟

实现

/* 树的孩子兄弟表示法结构定义 */
typedef struct CSNode
{
	TElemType data;	
	struct CSNode *firstchild,*rightsib;	
} CSNode,*CSTree;

二叉树（Binary Tree）

二叉树特点

每个结点最多有两棵子树（二叉树中不存在「度」大于2的结点）
子树有左右之分，其次序不能颠倒
二叉树可以是空集，根可以有空的左子树或空的右子树

二叉树不是「树」（的特殊情况）

二叉树是树型结构，但「二叉树」是「树」是两种不同的数据结构
二叉树结点的子树要区分左子树和右子树，即使只有一棵子树也要区分，说明它是左子树，还是右子树
树当结点只有一个「孩子」时，就无须区分它和左还是右的次序。因此，二者不同

二叉树每个结点位置或者说次序都是固定的，可以是空，但是不可以说它没有位置
而树的结点位置是相对于别的结点来说的，没有别的结点时，它就无所谓左右了

二叉树的5种基本形态

二叉树的性质

在二叉树的第 i 层上最多有 2ⁱ⁻¹ 个结点（i >= 1），最少 1 个结点
深度为 k 的二叉树最多有 2ᵏ - 1 个结点（k >= 1），最少 k 个结点
对任何一棵二叉树，如果其终端结点数为 n₀，度为2的结点数为 n₂，则 n₀ = n + 1
具有n个结点的完全二叉树的深度为[log₂n] + 1(高斯取整)
如果对一棵有n个结点的完全二叉树的结点按层序编号，对任意结点i有：
- 如果 i = 1，则i是二叉树的根，无双亲；如果 i > 1，则双亲为[i / 2]
- 如果 2i > n，则结点i是叶子结点，否则其左孩子是结点 2i
- 如果 2i + 1 > n,则结点i是叶子结点，否则其右孩子为 2i + 1

特殊二叉树

斜树

左斜树

右斜树

满二叉树

一棵深度为 k，且二叉树最多有 2ᵏ - 1 个结点的二叉树
特点
- 每一层上的结点数都是最大结点数，即每层都满
- 叶子结点全在最底层

完全二叉树

对一棵具有 n 个结点的二叉树按层序编号，如果编号为 i(1 <= i <= n) 的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中的位置完全相同，则这棵二叉树称为完全二叉树
满二叉树一定是完全二叉树，完全二叉树不一定是满的
特点
- 叶子结点只能出现在最下两层
- 最下层的叶子一定集中在左部连续位置
- 倒数二层，若有叶子结点，一定都在右部连续位置
- 如果结点度为1，则该结点只有左「孩子」，即不存在只有右子树的囚；
- 同样结点数的二叉树，完全二叉树的深度最小

完全二叉树

非完全二叉树

树1，结点5没有左子树，却有右子树，使得按层序编号的第10个编号空挡了
树2，结点3没有子树，使得6、7编号的位置空挡了

二叉树的抽象数据类型定义

ADT Tree{
Data
   树是由一个根结点和若干棵子树构成的。树中结点具有相同的数据类型及层次关系。
Operation
   InitTree(*T) :构造空树T
   DestroyTree(*T): 销毁树
   CreateTree(*T, definition):按definition中给出树的定义来构造树
   ClearTree(*T): 清空树
   TreeEmpty(*T): 空树返回true
   TreeDepth(*T): 返回T的深度
   Root(*T): 返回T的根结
   Value(T, cur_e): cur_e是树T中的一个结点，返回此结点的值
   Assign(T, cur-e, value): 给树T的结点cur_e赋值为value
   Parent(T, cur_e): 若cur_e不是根结点，则返回它的双亲
   LeftChild(T, cur_e): 若cur_e是树T的非叶结点，则返回它的最左孩子，否则返回空。
   RightSibling(T, cur_e): 若cur_e有右兄弟，则返回右兄弟，否则返回空。
   InsertChild(*T, *p, i, c):其中p指向树T的某个结点，i为所指结点p的度加上1，若非空树c与T不相交，操作结果为插入c为树T中p指向结点的第i棵子树。
   DeleteChild(*T, *p, i): 其中p为指向树T的某个结点，i为所指结点p的度，操作结果为删除T中P所指向结点的第i棵子树。
}endADT

二叉树的链式存储结构

二叉树每个结点最多有两个孩子，所以它有一个数据域和两个指针域
- data：数据域
- lchild：指针域，左孩子的指针
- rchild：指针域，右孩子的指针
这样的链表叫作二叉链表

二叉链表存储结构

/* 二叉链表结点结构定义 */
typedef struct BiTNode  			/* 结点结构 */
{
	TElemType data;					/* 结点数据 */
	struct BiTNode* lchild, * rchild; 	/* 左右孩子指针 */
}BiTNode, * BiTree;

遍历二叉树

二叉树的遍历（traversing binary tree）：从根结点出发，按照某种次序依次访问二叉树中所有的结点，使得每个结点被访问一次且仅被访问一次

遍历目的：得到树中所有结点的一个线性排列

遍历用途：它是树结构插入、删除、修改、查找和排序运算的前提，是二叉树一切运算的基础和核心

先序遍历（根左右，DLR）

若二叉树为空，则空操作；否则

访问根结点
先序遍历左子树
先序遍历右子树

先序遍历算法实现

void PreOrderTraverse(BiTree T)
{
	if (T == NULL)return; // 空二叉树
	else
	{
		printf("%c", T->data); /* 显示结点数据，可以更改为其它对结点操作 */
		PreOrderTraverse(T->lchild); /* 再先序遍历左子树 */
		PreOrderTraverse(T->rchild); /* 最后先序遍历右子树 */
	}
}

遍历流程

从根结点 A 开始，一直遍历左子树
直到 B 的左子树为空，返回，遍历右子树

访问 B 的右子树的根结点 D
访问根结点 D 的左子树，为空，返回
访问根结点 D 的右子树，为空，返回。
以 D 为根结点的 DLR 顺序结束，返回B的pre(T→R)处。以 B 为根结点的 DLR 顺序结束，返回 A 的pre(T→L)处。
之后继续访问 A 的右子树

中序遍历（左根右，LDR）

若二叉树为空，则空操作；否则

中序遍历左子树
访问根结点
中序遍历右子树

中序遍历算法实现

void InOrderTraverse(BiTree T)
{
	if (T == NULL) return; /* 空二叉数 */
	else 
	{
		InOrderTraverse(T->lchild); /* 中序遍历左子树 */
		printf("%c", T->data);		/* 显示结点数据，可以更改为其它对结点操作 */
		InOrderTraverse(T->rchild); /* 最后中序遍历右子树 */
	}
}

后序遍历（左右根，LRD）

若二叉树为空，则空操作；否则

后序遍历左子树
后序遍历右子树
访问根结点

后序遍历算法实现

void PostOrderTraverse(BiTree T)
{
	if (T == NULL)return;
	else
	{
		PostOrderTraverse(T->lchild); 	/* 先后序遍历左子树  */
		PostOrderTraverse(T->rchild); 	/* 再后序遍历右子树  */
		printf("%c", T->data);			/* 显示结点数据，可以更改为其它对结点操作 */
	}
}

例1：写出下图二叉树的各种遍历顺序

写出下图二叉树的各种遍历顺序

先序：A B D G C E H F
中序：D G B A E H C F
后序：G D B H E F C A

例2：用二叉树表示算术表达式

用二叉树表示算术表达式

先序：- + a * b - c d / e f
表达式的前缀表示（波兰式）
中序：a + b * c - d - e / f
表达式的中缀表达
后序：a b c d - * + e f / -
表达式的后缀表示（逆波兰式）

例3：已知先序和中序序列求二叉树

已知先序和中序序列求二叉树

答

思路

因为先序顺序为DLR，所以A一定为根
因为中序顺序为LDR，所以A左边的C D B F E一定在左子树，A右侧的I H G J一定在右子树

同理先序中，A旁边的B，为左子树的根。C D就在B的左子树，F E就在B的右子树

在先序中，因为 F 已经是在 B 的右子树中了，所以 G 就是 A 的右子树的根

由先序知，C 是 B 左子树的根
由中序知，D 是 C 的右子树，所以 C 的左子树为空

同理

二叉树的建立

一个遍历序列无法确定唯一的二叉树
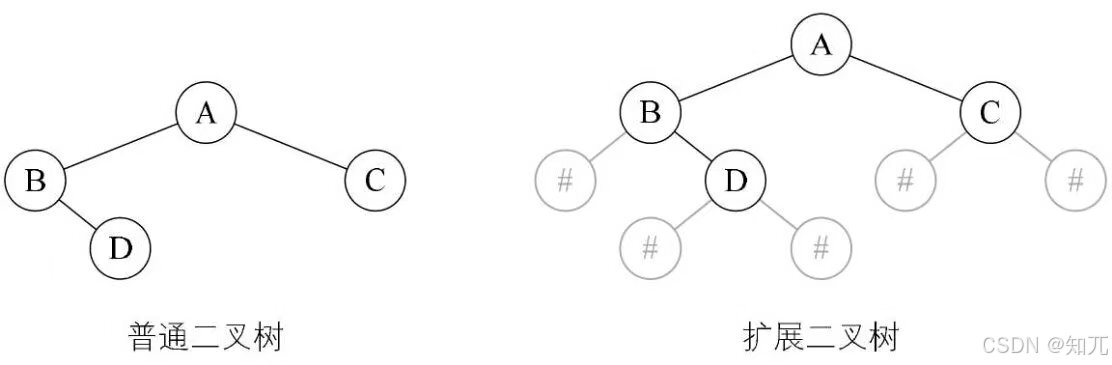
- 为了让二叉树的每个节点确认是否有左右孩子，对其进行扩展
在二叉树的每个结点的空指针引出一个虚结点，其值为一特定值，如果#
我们称这种处理后的二叉树为原二叉树的扩展二叉树

先序遍历序列为AB#D##C##

二叉树建立算法

/* 按前序输入二叉树中结点的值（一个字符） */
/* #表示空树，构造二叉链表表示二叉树T。 */
void CreateBiTree(BiTree* T)
{
	TElemType ch;

	scanf("%c", &ch);

	if (ch == '#')
		*T = NULL;
	else
	{
		*T = (BiTree)malloc(sizeof(BiTNode));
		if (!*T)
			exit(OVERFLOW);
		(*T)->data = ch; 					/* 生成根结点 */
		CreateBiTree(&(*T)->lchild); 	/* 构造左子树 */
		CreateBiTree(&(*T)->rchild); 	/* 构造右子树 */
	}
}

线索二叉树

Q：如何寻找特定遍历序列中二叉树结点的前驱和后继？
A：充分利用空指针域，使其存放指向结点在某种遍历次序下的前驱和后继的地址
把指向前驱和后继的指针称为线索
- 加上线索的二叉链表称为线索链表，相应的二叉树称为线索二叉树(Threaded Binary Tree)
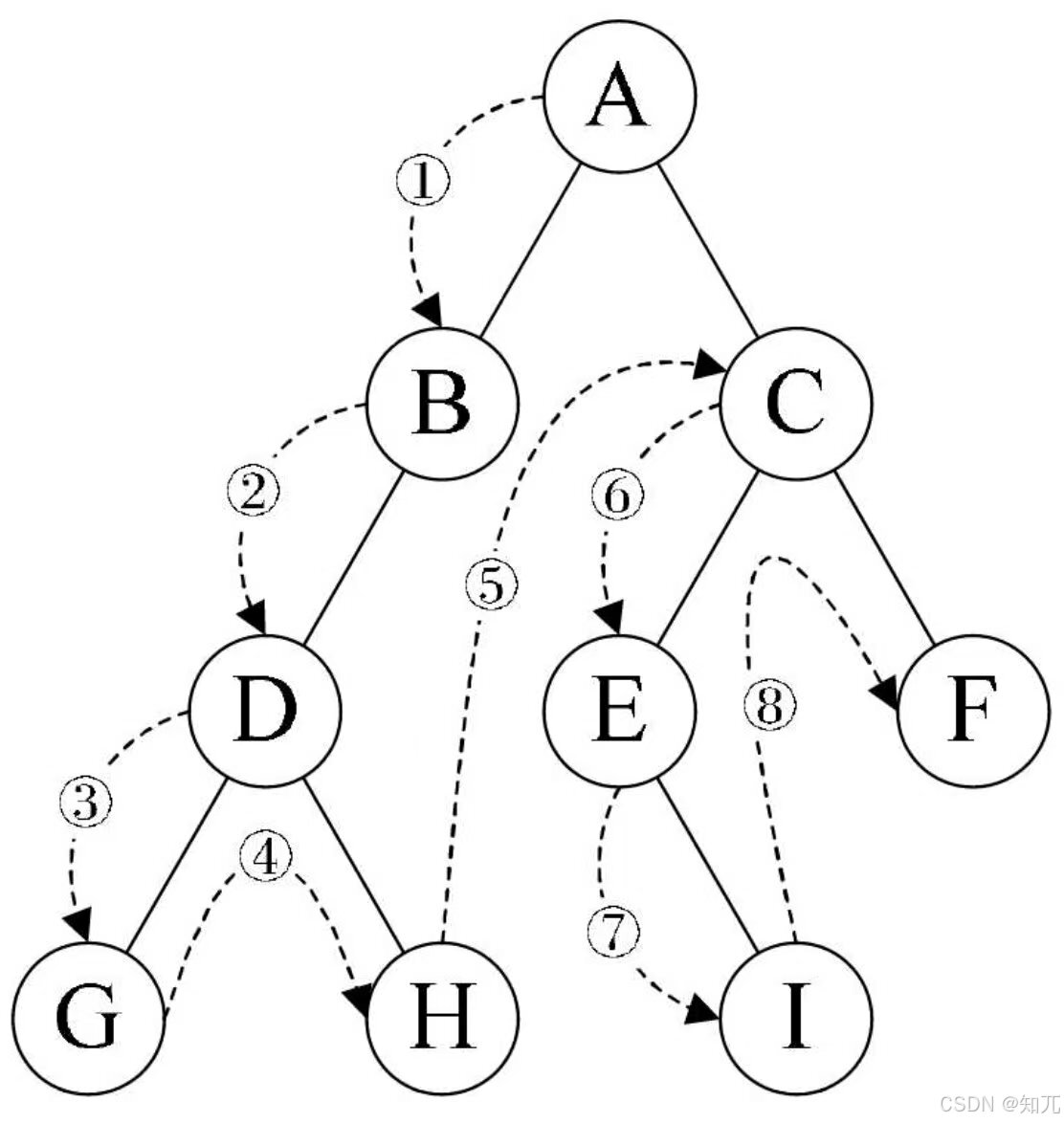
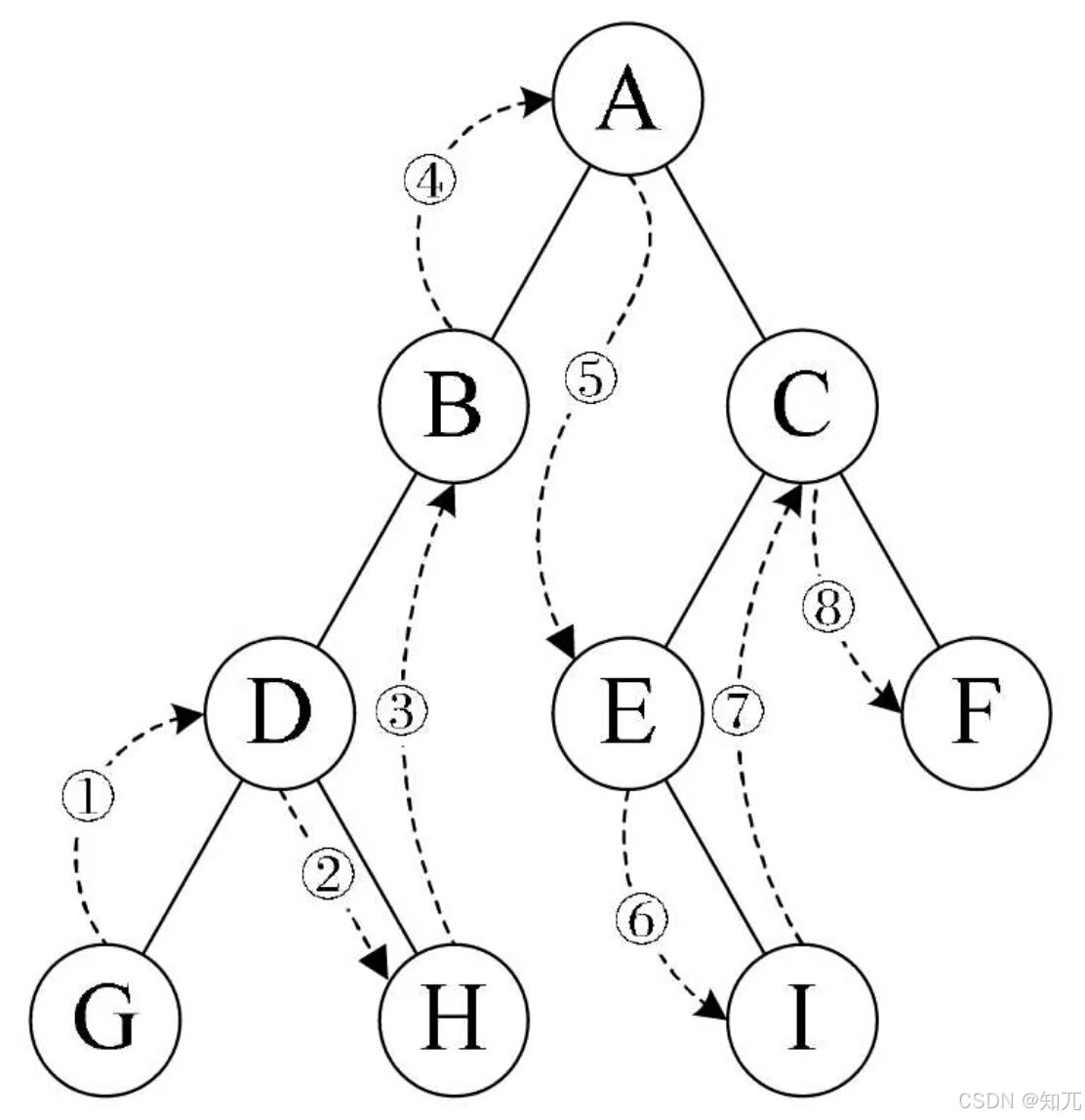
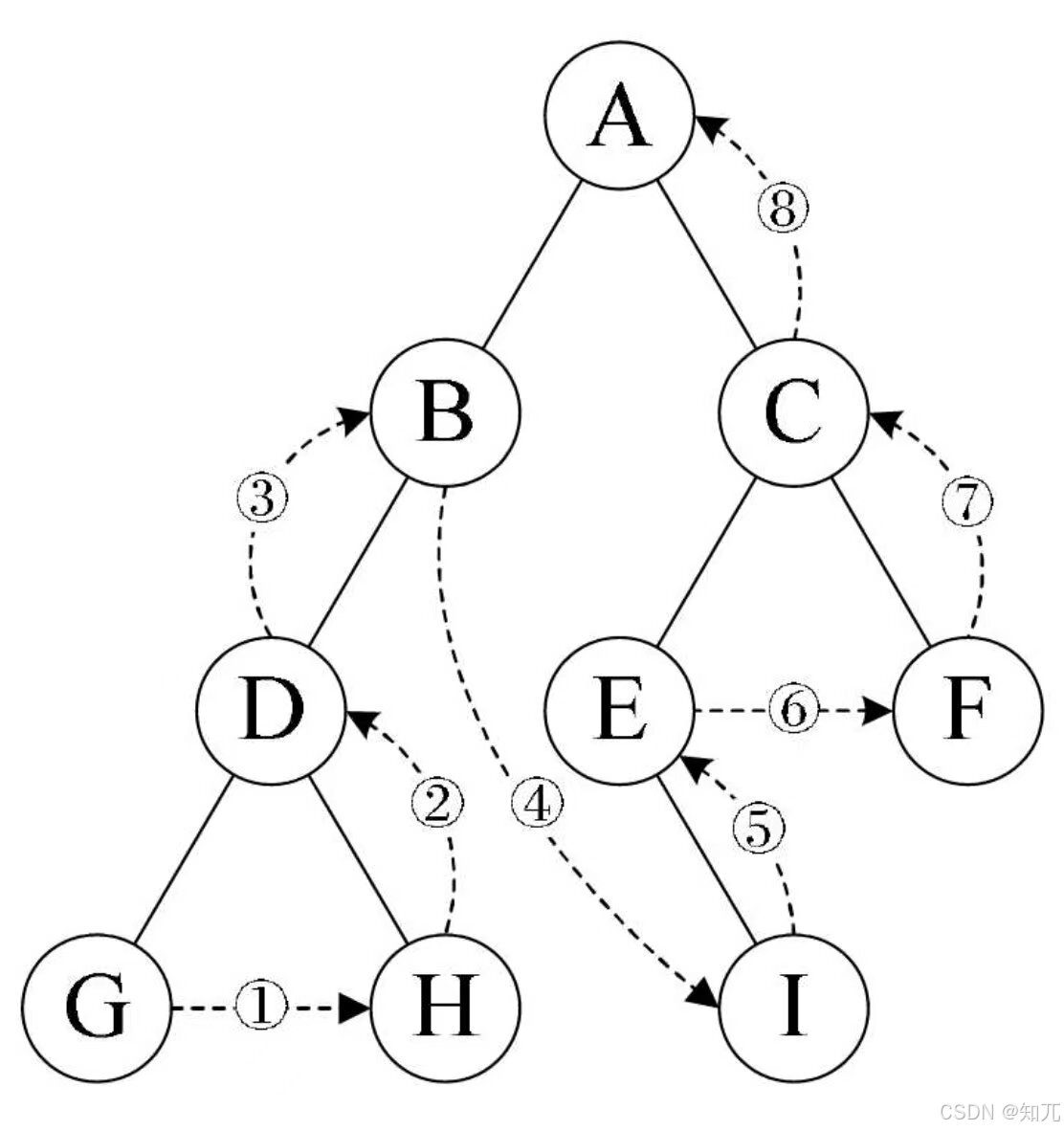
线索化：对二叉树以某种次序遍历使其变为线索二叉树的过程，这个过程将二叉树转化为了双向链

空心箭头为前驱
黑箭头为后继

为明确lchild（rchild）存放是孩子还是前驱，需要设置两个标志域，ltag 和 rtag，通常为0或1
- tag为0表示孩子，为1表示前驱或后继

结点的结构

修改后的二叉链表图

线索二叉树的结构定义

/* 二叉树的二叉线索存储结构定义 */
typedef char TElemType;
typedef enum { Link, Thread } PointerTag;	
/* Link==0表示指向左右孩子指针, */
/* Thread==1表示指向前驱或后继的线索 */

typedef  struct BiThrNode				/* 二叉线索存储结点结构 */
{
	TElemType data;						/* 结点数据 */
	struct BiThrNode* lchild, * rchild;	/* 左右孩子指针 */
	PointerTag LTag;
	PointerTag RTag;					/* 左右标志 */
} BiThrNode, * BiThrTree;

typedef enum { Link, Thread } PointerTag

typedef enum 用于定义了一个名为 PointerTag 的枚举类型，它包含两个枚举值：Link 和 Thread
- 在枚举中，如果不显式地指定值，编译器会从0开始自动为第一个枚举值赋值，然后每个后续的枚举值会自动递增1
- Link：当 PointerTag 的值为 Link（值为0）时，表示对应的指针（lchild 或 rchild）指向的是二叉树中的左右孩子节点
- Thread：当 PointerTag 的值为 Thread（值为1）时，表示对应的指针指向的是线索二叉树中的前驱或后继节点

树与二叉树的转换

了解

给定一棵树，可以找到唯一的一棵二叉树与之对应
因为一棵树的存储结构是唯一的，解释成二叉树的二叉链表也是唯一的，对应的二叉树也是唯一的

树和二叉树的转换（兄弟相连留长子）

加线：所有兄弟结点之间加一条连线
去线：只保留与第一个孩子结点的连线
层次调整：顺时针旋转，第一个孩子是二叉树结点的左孩子，从兄弟转换过来的孩子是结点的右孩

树变二叉树，根节点的右子树一定为空

例：将树转换成二叉树

加线：所有兄弟结点之间加一条连线

去线：只保留与第一个孩子结点的连线

层次调整

二叉树转换成树（左孩右右连双亲，去掉原来右孩线）

加线：若p结点是双亲结点的左孩子，则将p的右孩子，右孩子的右孩子……沿分支找到的所有右孩子，都与p的双亲用线连起来
抹线：抹掉原二叉树中双亲与右孩子之间的连线
调整：将结点按层次排列，形成树结构

例：将二叉数转换成树

加线：若p结点是双亲结点的左孩子，则将p的右孩子，右孩子的右孩子……沿分支找到的所有右孩子，都与p的双亲用线连起来

抹线：抹掉原二叉树中双亲与右孩子之间的连线

调整

森林转换成二叉树（树变二叉根相连）

（二叉树与多棵树之间的关系）

将各棵树分别转换成二叉树
将每棵树的根结点用线相连
以第一棵树根结点为二叉树的根，再以根结点为轴心，顺时针旋转，构成二叉树型结构

例：将森林转换成二叉树

将各棵树分别转换成二叉树

将每棵树的根结点用线相连

以第一棵树根结点为二叉树的根，再以根结点为轴心，顺时针旋转，构成二叉树型结构

二叉树转换成森林（去掉全部右孩线，孤立二叉再还原）

抹线：将二叉树中根结点与其右孩子连线，及沿右分支搜索到的所有右孩子间连线全部抹掉，使之变成孤立的二叉树
还原：将孤立的二叉树还原成树

例：二叉树转换成森林

抹线：将二叉树中根结点与其右孩子连线，及沿右分支搜索到的所有右孩子间连线全部抹掉，使之变成孤立的二叉树

还原：将孤立的二叉树还原成树

树的遍历

先根（次序）遍历

若树不空，则先访问根结点，然后依次先根遍历各棵子树

后根（次序）遍历

若树不空，则先依次后根遍历各棵子树，然后访问根结点

按层次遍历

若树不空，则自上而下自左至右访问树中每个结点

例

先根遍历：A B C D E
后根遍历：B D C E A
按层次遍历：A B C E D

森林的遍历

将森林看作由三部分构成：

森林中第一棵树的根结点
森林中第一棵树的子树森林
森林中其他树构成的森林

先序遍历

若森林不空，则

访问森林中第一棵树的根结点
先序遍历森林中第一棵树的子树森林
先序遍历森林中（除第一棵树之外）其余树构成的森林

（即：依次从左至右对森林中的每一棵树进行先根遍历）

中序遍历

若森林不空，则

中序遍历森林中第一棵树的子树森林
访问森林中第一棵树的根结点
中序遍历森林中（除第一棵树之外）其余树构成的森林

（即：依次从左至右对森林中的每一棵树进行后根遍历）

例

先序遍历（1→2→3）：A B C D E F G H I J
中序遍历（2→1→3）：B C D A F E H J I G

线性结构	树结构
第一个数据元素：无前驱	根结点（只有一个）：无双亲
最后一个数据元素：无后继	叶结点（可以多个）：无孩子
中间元素：一个前驱、一个后继	中间结点：一个双亲、多个孩子
一对一	一对多

数据结构-树、二叉树，森林，及其转换

概念

结点分类

根结点

结点的度（De-gree）

树的度

结点间关系

孩子（Child）、双亲（Parent）

兄弟（Sibing）、堂兄弟（Cousins）

祖先（ancestor)、 子孙（descendant）

结点的层次（Level）、树的深度（Depth）

有序树、无序树、森林（Forest）

总结

线性结构和树结构的差异

树的存储结构

双亲表示法

实现

孩子表示法（孩子链表）

实现

孩子兄弟表示法

实现

二叉树（Binary Tree）

二叉树特点

二叉树不是「树」（的特殊情况）

二叉树的5种基本形态

二叉树的性质

特殊二叉树

斜树

满二叉树

完全二叉树

二叉树的抽象数据类型定义

二叉树的链式存储结构

二叉链表存储结构

遍历二叉树

先序遍历（根左右，DLR）

先序遍历算法实现

遍历流程

中序遍历（左根右，LDR）

中序遍历算法实现

后序遍历（左右根，LRD）

后序遍历算法实现

例1：写出下图二叉树的各种遍历顺序

例2：用二叉树表示算术表达式

例3：已知先序和中序序列求二叉树

思路

二叉树的建立

二叉树建立算法

线索二叉树

线索二叉树的结构定义

typedef enum { Link, Thread } PointerTag

树与二叉树的转换

了解

树和二叉树的转换（兄弟相连留长子）

例：将树转换成二叉树

二叉树转换成树（左孩右右连双亲，去掉原来右孩线）

例：将二叉数转换成树

森林转换成二叉树（树变二叉根相连）

例：将森林转换成二叉树

二叉树转换成森林（去掉全部右孩线，孤立二叉再还原）

例：二叉树转换成森林

树的遍历

先根（次序）遍历

后根（次序）遍历

按层次遍历

例

森林的遍历

先序遍历

中序遍历

例

祖先（ancestor)、子孙（descendant）