二叉树的遍历方式-CSDN博客

本文链接：https://blog.csdn.net/2403_87297753/article/details/147481054

二叉树的遍历方式这里介绍三种：中序遍历（左根右），前序遍历（根左右），后序遍历（左右根），三者的遍历顺序不同，但是遍历的思想是相同的，都灵活地运用了递归

1.1中序遍历（左根右）

如上图，遍历上述二叉树，用中序遍历方法，则得到的遍历结果为：NULL, D, NULL, B, NULL, A, NULL, E, NULL, C, NULL, F, NULL，因为中序遍历的遍历顺序是左根右，严格按照这个顺序来遍历，并且运用了递归的方法，代码如下：

1.1.1结构的定义链式二叉树

typedef char BTDataType;//定义数据结构类型
typedef struct BinaryTreeNode
{
   BTDatatype data;
   struct BinaryTreeNode* left;
   struct BinaryTreeNode* right;
}BTNode;

1.1.2中序遍历—左根右

void inOrder(BTNode* root)
{
   if(root == NULL)//当然也可以用assert来断言
   {
      printf("NULL");
      return;
   }
   inOrder(root->left);//不断地向下寻找左结点
   printf("%c",root->data);//打印结点
   inOrder(root->right);//寻找右结点
}

这里运用了递归的思想，不断地向下寻找所需要的结点，如果遇到空结点，则返回，每次调用函数就会创建一个函数栈桢，函数运行完毕，则消除该函数栈桢。

1.1.3测试该函数的执行

BTNode* buyNode(char x)//创建一个函数用来创造结点
{
    BTNode* node = (BTNode*)malloc(sizeof(BTNode))
    node->data = x;
    node->left = node->right = NULL;
    return node;
}

BTNode* createBinaryTree()//创建原始的数据
{
    BTNode* nodeA = buyNode('A');
	BTNode* nodeB = buyNode('B');
	BTNode* nodeC = buyNode('C');
	BTNode* nodeD = buyNode('D');
	BTNode* nodeE = buyNode('E');
	BTNode* nodeF = buyNode('F');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;

	return nodeA;
}

int main()
{
    BTNode* root = createBinaryTree();
    inOrder(root);
    return 0;
}

通过以上代码就可以实现中序遍历啦

1.2前序遍历（根左右）

同理如上二叉树，用前序遍历可以的到的遍历结果为：A, B, D, NULL, NULL, NULL, C, E, NULL, NULL, F, NULL, NULL,因为前序遍历运用的思想是根左右，所以严格先遍历根结点，再到左和右结点，并且同时也用了递归，代码如下：

1.2.1结构的定义链式二叉树

结构的定义与中序遍历的一样

1.2.2前序遍历—根左右

void preOrder(BTNode* root)
{
    if(root == NULL)
    {
       printf("NULL");
       return;
    }
}
    printf("%c",root->data);
    preOrder(root->left);//递归
    preOrder(root->right);//递归
}

因为是先遍历根结点，所以会先打印出根结点的数据，在用递归的方式去寻找左右结点，同样，每调用一次函数就创建一个函数栈桢，结束后销毁。

1.2.3测试函数运行

int main()
{
    BTNode* root = createBinaryTree();
    preOrder(root);
    return 0;
}

将main函数里面调用的函数修改一下就好啦，这样就可以完成前序遍历啦（测试中其他和中序遍历是一样的代码）

1.3后序遍历（左右根）

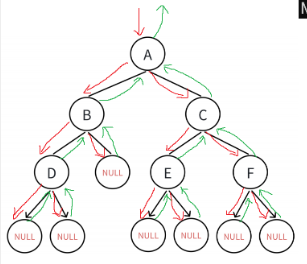
同理如上图二叉树，遍历结果为：NULL, NULL, D, NULL, B, NULL, NULL, E, NULL, NULL, F, C, A,因为后序遍历运用的思想是左右根，所以严格按照左结点到右结点，再根结点，并且同时也用了递归，代码如下：

1.3.1结构的定义链式二叉树

和中序遍历一样哈

1.3.2后序遍历—左右根

void postOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	postOrder(root->left);
	postOrder(root->right);
	printf("%c ", root->data);
}

1.3.3测试函数运行

int main()
{
    BTNode* root = createBinaryTree();
    postOrder(root);
    return 0;
}