数据结构实验5-图

集美大学课程实验报告-实验5-图

项目名称	内容
课程名称	数据结构
班级	网安2412
指导教师	郑如滨
学生姓名	缪书华
学号	202421336060
实验项目名称	实验5-图
上机实践日期	2025.5.15
上机实践时间	2学时

---

一、目的（本次实验所涉及并要求掌握的知识点）

• 理解图的概念和基础知识
• 学习有向图的创建和遍历及基础操作
• 学习应用

---

二、实验内容与设计思想

题目1：图的创建—题目2：图的遍历

时间复杂度和空间复杂度

1. initGraph
   时间复杂度：O(n^2)
   空间复杂度：O(1)
2. addVertex
   时间复杂度：O(1)
   空间复杂度：O(1)
3. addEdge
   时间复杂度：O(1)
   空间复杂度：O(1)
4. printGraph
   时间复杂度：O(n^2)
   空间复杂度：O(1)
5. DFS
   时间复杂度：O(n)
   空间复杂度：O(n)
6. BFS
   时间复杂度：O(n)
   空间复杂度：O(n)

函数相关伪代码

// 图的初始化
initGraph 
    将G的顶点数vertexNum设置为n
    将G的边数arcNum设置为m
    遍历邻接矩阵adjMatrix的每一个元素，将其值设置为0
    end
// 添加顶点
addVertex
    将顶点字符vertex存储到G的vexs数组的index位置
    在G的vertexIndex映射中，将顶点字符vertex映射到索引index
	end
// 添加边
addEdge
    根据G的vertexIndex映射，获取顶点u的索引uIndex
    根据G的vertexIndex映射，获取顶点v的索引vIndex
    将G的邻接矩阵adjMatrix中uIndex行vIndex列的元素值设置为cost
    将G的邻接矩阵adjMatrix中vIndex行uIndex列的元素值设置为cost
	end
// 打印图
printGraph
    打印提示信息“顶点列表: ”
    遍历G的vexs数组，依次打印每个顶点字符
    换行
    打印提示信息“邻接矩阵: ”
    打印一个空格和制表符
    遍历G的vexs数组，依次打印每个顶点字符作为列标题
    换行
    遍历G的vexs数组，对于每个顶点字符：
        打印该顶点字符和一个空格
        再遍历G的vexs数组，对于每个顶点字符：
            打印G的邻接矩阵adjMatrix中对应位置的元素值和一个空格
        换行
	end
// 深度优先搜索
DFS
    将visited数组中start位置的元素设置为true，表示已访问
    将G的vexs数组中start位置的顶点字符添加到result字符串中
    遍历G的vexs数组，对于每个顶点字符对应的索引i：
        如果G的邻接矩阵adjMatrix中start行i列的元素值不为0，且visited数组中i位置的元素为false（未访问）：
            递归调用DFS函数，传入G、i、visited和result
	end
// 广度优先搜索
BFS
    创建一个整数类型的队列q
    将start入队到队列q中
    将visited数组中start位置的元素设置为true，表示已访问
    将G的vexs数组中start位置的顶点字符添加到result字符串中
    当队列q不为空时：
        取出队列q的队首元素，赋值给变量current
        将队首元素出队
        遍历G的vexs数组，对于每个顶点字符对应的索引i：
            如果G的邻接矩阵adjMatrix中current行i列的元素值不为0，且visited数组中i位置的元素为false（未访问）：
                将visited数组中i位置的元素设置为true
                将G的vexs数组中i位置的顶点字符添加到result字符串中
                将i入队到队列q中
	end
// 主函数
main函数：
    创建Graph类型的对象G
    读入顶点数n和边数m
    调用initGraph进行图的初始化
    输入每个顶点的字符，依次调用addVertex函数，传入G、顶点字符和对应的索引进行顶点添加
    输入每条边的两个顶点字符和边的权值，依次调用addEdge函数，传入G、顶点字符和权值进行边的添加
    调用printGraph函数，传入G进行图的打印
    创建一个布尔数组visited，大小为MAX_VERTEX，并初始化为false
    创建一个空字符串dfsResultA
    调用DFS函数，传入G、从G的vertexIndex映射中获取的字符'a'对应的索引、visited和dfsResultA
    打印提示信息“从A节点进行DFS，遍历结果为: ”和dfsResultA
    将visited数组重新初始化为false
    创建一个空字符串dfsResultF
    调用DFS函数，传入G、从G的vertexIndex映射中获取的字符'f'对应的索引、visited和dfsResultF
    打印提示信息“从F节点进行DFS，遍历结果为: ”和dfsResultF
    将visited数组重新初始化为false
    创建一个空字符串bfsResultF
    调用BFS函数，传入G、从G的vertexIndex映射中获取的字符'f'对应的索引、visited和bfsResultF
    打印提示信息“从F节点进行BFS，遍历结果为: ”和bfsResultF
    返回0
    end

函数代码

#include <iostream>
#include <cstring>
#include <map>
#include <queue>
using namespace std;

#define MAX_VERTEX 100

struct Graph {
    int vertexNum;
    int arcNum;
    char vexs[MAX_VERTEX];  // 存储顶点名称
    int adjMatrix[MAX_VERTEX][MAX_VERTEX];
    map<char, int> vertexIndex;  // 顶点名称到索引的映射
};
void initGraph(Graph& G, int n, int m) {
    G.vertexNum = n;
    G.arcNum = m;
    memset(G.adjMatrix, 0, sizeof(G.adjMatrix));
}
void addVertex(Graph& G, char vertex, int index) {
    G.vexs[index] = vertex;
    G.vertexIndex[vertex] = index;
}
void addEdge(Graph& G, char u, char v, int cost) {
    int uIndex = G.vertexIndex[u];
    int vIndex = G.vertexIndex[v];
    G.adjMatrix[uIndex][vIndex] = cost;
    G.adjMatrix[vIndex][uIndex] = cost;
}
void printGraph(Graph& G) {
    cout << "顶点列表: ";
    for (int i = 0; i < G.vertexNum; ++i) {
        cout << G.vexs[i] << " ";
    }
    cout << endl;

    cout << "邻接矩阵: " << endl;
    cout << "  ";
    for (int i = 0; i < G.vertexNum; ++i) {
        cout << G.vexs[i] << " ";
    }
    cout << endl;
    for (int i = 0; i < G.vertexNum; ++i) {
        cout << G.vexs[i] << " ";
        for (int j = 0; j < G.vertexNum; ++j) {
            cout << G.adjMatrix[i][j] << " ";
        }
        cout << endl;
    }
}
void DFS(Graph& G, int start, bool visited[], string& result) {
    visited[start] = true;
    result += G.vexs[start];

    for (int i = 0; i < G.vertexNum; ++i) {
        if (G.adjMatrix[start][i] != 0 && !visited[i]) {
            DFS(G, i, visited, result);
        }
    }
}
void BFS(Graph& G, int start, bool visited[], string& result) {
    queue<int> q;
    q.push(start);
    visited[start] = true;
    result += G.vexs[start];

    while (!q.empty()) {
        int current = q.front();
        q.pop();

        for (int i = 0; i < G.vertexNum; ++i) {
            if (G.adjMatrix[current][i] != 0 && !visited[i]) {
                visited[i] = true;
                result += G.vexs[i];
                q.push(i);
            }
        }
    }
}
int main() {
    Graph G;
    int n, m;
    cout << "输入顶点数和边数: ";
    cin >> n >> m;
    initGraph(G, n, m);

    cout << "输入顶点: ";
    for (int i = 0; i < n; ++i) {
        char vertex;
        cin >> vertex;
        addVertex(G, vertex, i);
    }

    cout << "输入边: " << endl;
    for (int i = 0; i < m; ++i) {
        char u, v;
        int cost;
        cin >> u >> v >> cost;
        addEdge(G, u, v, cost);
    }

    printGraph(G);

    // 从A节点进行DFS
    bool visited[MAX_VERTEX] = { false };
    string dfsResultA;
    DFS(G, G.vertexIndex['a'], visited, dfsResultA);
    cout << "从A节点进行DFS，遍历结果为: " << dfsResultA << endl;

    // 从F节点进行DFS
    memset(visited, false, sizeof(visited));
    string dfsResultF;
    DFS(G, G.vertexIndex['f'], visited, dfsResultF);
    cout << "从F节点进行DFS，遍历结果为: " << dfsResultF << endl;

    // 从F节点进行BFS
    memset(visited, false, sizeof(visited));
    string bfsResultF;
    BFS(G, G.vertexIndex['f'], visited, bfsResultF);
    cout << "从F节点进行BFS，遍历结果为: " << bfsResultF << endl;

    return 0;
}

---

题目3：图着色问题

时间复杂度和空间复杂度

1. main
   时间复杂度：O(E+N(V+E))
   空间复杂度：O(E+NV)
   函数相关伪代码

main() {
    读取顶点数 V，边数 E，颜色数 K
    创建一个大小为 V + 1 的二维向量 adj 用于存储邻接表（索引从 1 到 V）
    // 构建邻接表
    for i 从 0 到 E - 1  {
        读取边的两个端点 u 和 v
        将 v 添加到 adj[u] 中
        将 u 添加到 adj[v] 中
    }
    读取方案数 N
    // 处理每个颜色分配方案
    for i 从 0 到 N - 1  {
        创建一个大小为 V 的向量 colors 用于存储顶点颜色
        创建一个无序集合 color_set 用于存储颜色集合
        // 读取顶点颜色并插入到颜色集合中
        for j 从 0 到 V - 1  {
            读取 colors[j]
            将 colors[j] 插入到 color_set 中
        }
        // 检查颜色集合大小是否等于 K
        如果 color_set 的大小不等于 K {
            输出 "No"
            继续下一个方案
        }
        设 valid 为 true
        // 检查相邻顶点颜色是否相同
        for u 从 1 到 V 循环 {
            for v 在 adj[u] 中循环 {
                如果 colors[u - 1] 等于 colors[v - 1] {
                    valid 设为 false
                    跳出内层循环
                }
            }
            如果 valid 为 false {
                跳出外层循环
            }
        }
        // 输出结果
        如果 valid 为 true {
            输出 Yes
        } else {
            输出 No
        }
    }
    return 0
}

函数代码

#include <iostream>
#include <vector>
#include <unordered_set>

using namespace std;

int main() {
    int V, E, K;
    cin >> V >> E >> K;
    vector<vector<int>> adj(V + 1);  // 从1到V
    for (int i = 0; i < E; ++i) {
        int u, v;
        cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
    int N;
    cin >> N;
    for (int i = 0; i < N; ++i) {
        vector<int> colors(V);
        unordered_set<int> color_set;
        for (int j = 0; j < V; ++j) {
            cin >> colors[j];
            color_set.insert(colors[j]);
        }

        if (color_set.size() != K) {
            cout << "No" << endl;
            continue;
        }
        bool valid = true;
        for (int u = 1; u <= V; ++u) {
            for (int v : adj[u]) {
                if (colors[u - 1] == colors[v - 1]) {
                    valid = false;
                    break;
                }
            }
            if (!valid) break;
        }
        cout << (valid ? "Yes" : "No") << endl;
    }
    return 0;
}

题目4：公路村村通（最小生成树)

时间复杂度和空间复杂度

1. find
   时间复杂度：O(n)
   空间复杂度：O(1)
2. unite
   时间复杂度：O(n)
   空间复杂度：O(1)
   函数相关伪代码

// 查找函数
find(int u) {
    if parent[u] != u {
        parent[u] = find(parent[u]);
    }
    return parent[u];
}
// 合并函数
unite(int u, int v) {
    u = find(u);
    v = find(v);
    if u 等于 v {
        返回 false;
    }
    parent[v] = u;
    返回 true;
}
// 主函数
main() {
    读取顶点数 n 和边数 m
    创建一个大小为 m 的向量 edges 用于存储边的信息
    // 读取每条边的信息
    for i 从 0 到 m - 1 循环 {
        读取 edges[i].u, edges[i].v, edges[i].cost
    }
    // 对边集进行排序
    对 edges 进行排序

    // 初始化并查集的父节点数组
    parent 调整大小为 n + 1
    for i 从 1 到 n  {
        parent[i] = i;
    }

    设 total_cost 为 0
    设 connected 为 0

    // 遍历排序后的边集
    for 每条边 e 在 edges 中{
        if unite(e.u, e.v) {
            total_cost += e.cost
            connected++
            if connected 等于 n - 1 {
                break;
            }
        }
    }
    // 输出结果
    if connected 等于 n - 1 {
        输出 total_cost
    } else {
        输出 -1
    }

    返回 0
}

函数代码

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

struct Edge {
    int u, v, cost;
    bool operator<(const Edge &other) const {
        return cost < other.cost;
    }
};
vector<int> parent;
int find(int u) {
    if (parent[u] != u) {
        parent[u] = find(parent[u]);
    }
    return parent[u];
}
bool unite(int u, int v) {
    u = find(u);
    v = find(v);
    if (u == v) return false;
    parent[v] = u;
    return true;
}
int main() {
    int n, m;
    cin >> n >> m;
    vector<Edge> edges(m);
    for (int i = 0; i < m; ++i) {
        cin >> edges[i].u >> edges[i].v >> edges[i].cost;
    }
    sort(edges.begin(), edges.end());
    parent.resize(n + 1);
    for (int i = 1; i <= n; ++i) {
        parent[i] = i;
    }
    int total_cost = 0;
    int connected = 0;
    for (const Edge &e : edges) {
        if (unite(e.u, e.v)) {
            total_cost += e.cost;
            connected++;
            if (connected == n - 1) break;
        }
    }
    if (connected == n - 1) {
        cout << total_cost << endl;
    } else {
        cout << -1 << endl;
    }
    return 0;
}

三、实验使用环境（本次实验所使用的平台和相关软件）

以下请根据实际情况编写

• 操作系统：Windows 11专业版
• 编程语言：C++
• 开发工具：Visual Studio 2022

---

四、实验步骤和调试过程（实验步骤、测试数据设计、测试结果分析）

题目1：图的创建—题目2：图的遍历

本机运行截图

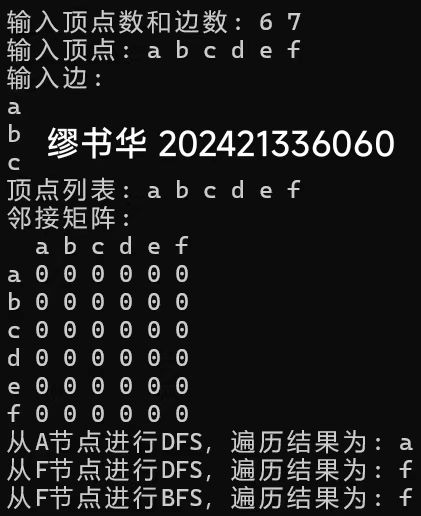
题目3：图着色问题

PTA提交截图

题目4：公路村村通（最小生成树)

PTA提交截图

---

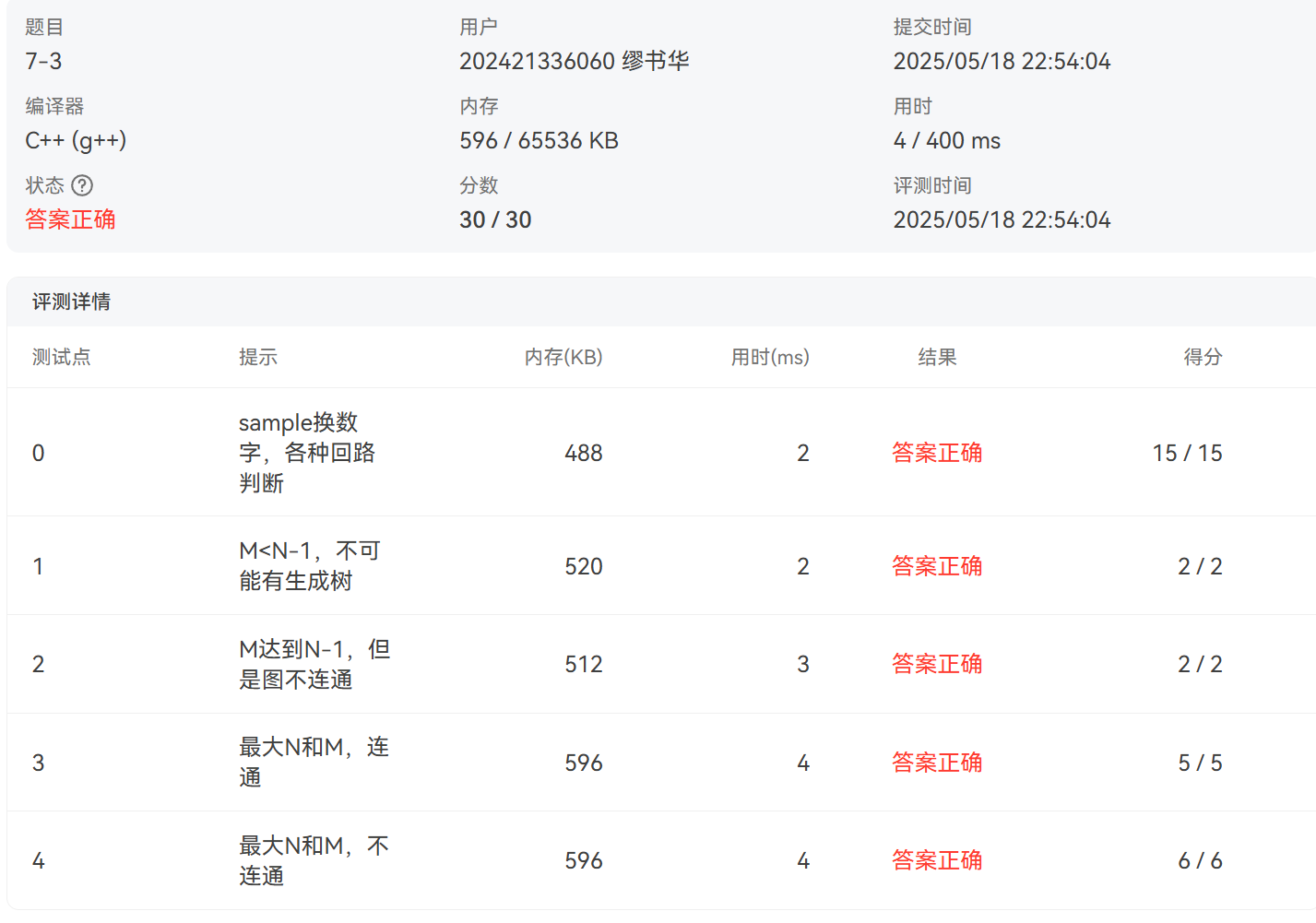
五、实验小结（实验中遇到的问题及解决过程、实验体会和收获）

遇到的问题及解决方法：

1. 问题：对图的创建不熟悉，没有完全理解邻接表和邻接矩阵
   • 解决方法：查询csdn文章进一步学习

实验体会和收获：

• 学会了图的创建和遍历，理解了邻接表和邻接矩阵
• 掌握了图的基础操作并应用图解决基础问题

---

六、附件（参考文献和相关资料）

1. 图的创建
2. 实验5-图