直线的投影————2

1. 直线与投影面的关系

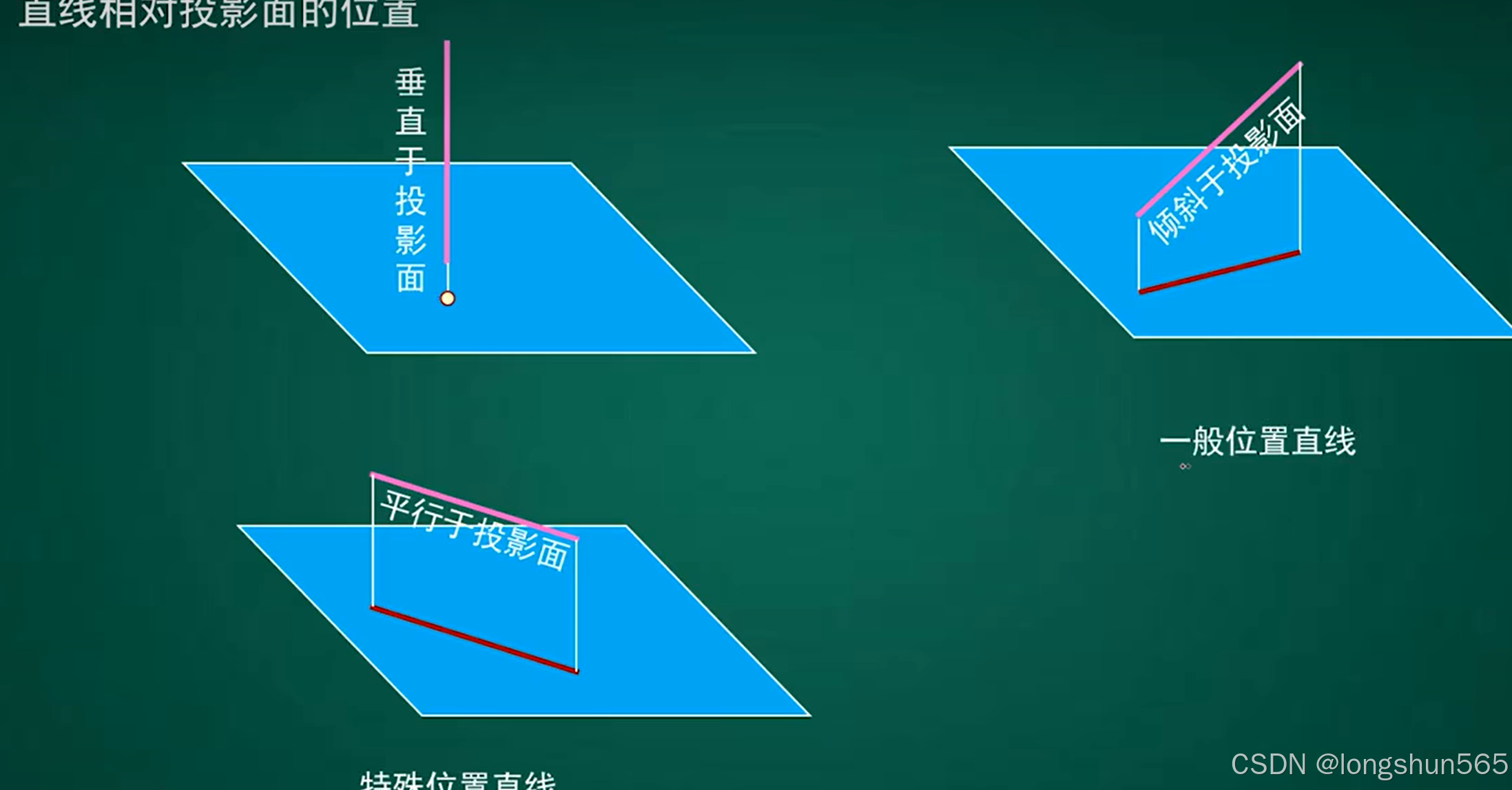
判断：

2-第二章 直线的投影-1_哔哩哔哩_bilibili

八分钟那里，有必要听一听他的讲解

有一个要注意的：如果是一般位置直线，就不可能有一个投影面垂直于一个坐标轴，所以如果出现既有平行于坐标轴的又有不平行于坐标轴的，直接判断为平行线

怎么理解他的这种以oxyz轴为判断的理论呢？

两个投影面的直线不要选取同一个轴作为参考

比如：

第二行第一个，

如果判断为两个都是平行ox轴，那就无法得出答案，要判断为一个垂直oz轴一个垂直oy轴才行

第二行第二个，不能判断都平行于oz轴，应该判断为垂直ox和oy轴

第三行第一个，应判断为垂直oz轴和oy轴，

第三行第二个，应判断为平行于ox轴和oy轴，

第三行第三个，应判断为平行于ox轴和oz轴，而不是都垂直于oy轴

2. 求一般直线的实长以及与投影面的夹角

本质就是找出两个直角边，至于你想怎么在三视图上画出来，都可以

练习：

要求 s 点坐标，只需要知道deita y 

因为 s 一定在那条垂直线上（点的投影规律）

直角三角形求deita y 就行了

答案在十五分钟那里，2-第二章 直线的投影-1_哔哩哔哩_bilibili

再练一个

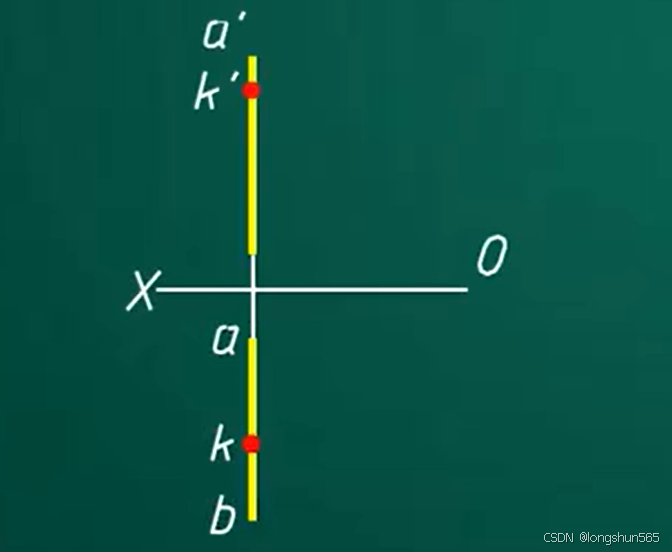
3. 属于直线上的点

判断一个点是否属于直线————是否等分线段

在判断是否相交问题里面很常用

可以直接量取 ab 的长度再等分，但是这样的话精确度不搞，因为ab 不一定是5的倍数，但是任意做的就可以是

也可以通过补图的方式

4. 两直线的位置

4.1 两直线平行

性质：

判定：

由于没有交点，所以考虑是否共面，共面就是平行

当然补第三面投影也是可以的

4.2 两直线相交

相交意味着交点在两个直线上（且成比例），即交点满足点的投影规律

明显，点让ab成比例但是不让cd成比例，所以点不在cd上

补图也可以

总结：如果是两条一般位置直线的话，只需要看两个投影面，否则需要三个（或者根据点分别在不在两条直线上，也就是比例来判断）

4.3 两直线交叉

利用相交的知识来看

明显不相交，也不平行，所以是异面（交叉）

4.4 两直线可见性

水平面的投影点从z轴看，正平面从y轴，侧平面从x轴

4.4 直角投影定理

4.4.1 垂直相交两直线的投影

一二是互逆的定理

注意：平行于哪个投影面，直角就在哪个投影面上

练习：

4.4.2 垂直交叉两直线的投影

练习：

欲求公垂线，先一个一个求垂直（运用垂直相交两直线的知识）

找初步确定L的位置之后，再运用点的投影规律，确保sl在同一直线上