数据结构之 AVL树（内附C++实现）

Ⅰ、介绍AVL树

AVL树是苏联的科学家G. M. Adelson-Velsky和E. M. Landis于1962年提出。我们知道二叉搜索树太特殊情况下时间复杂度会从O(logN) 降到 O(N) ，这对效率的影响很大但二叉搜索树这种结构很好，如何去改进才能使得他的时间复杂度不会降到O(N) ？这两位科学家提出通过控制左右子树的高度差来实现。

Ⅱ、AVL树的性质

1、AVL树的左右子树都是AVL树

2、AVL树的左右子树的高度差不会高于+1/-1

特别说明一下空树也是AVL树

Ⅲ、平衡因子的定义

这里我们通过控制平衡因子来判断现在的树是不是AVL树和来控制AVL树 ，当然我们也可以不通过平衡因子的方法来实现AVL树， 平衡因子 = 右子树的高度 - 左子树的高度（也可以是其他的方式 ，比如 左子树的高度 - 右子树的高度 ）。当平衡因子为2 / -2时我们去通过旋转的方式把这个树变成AVL树。

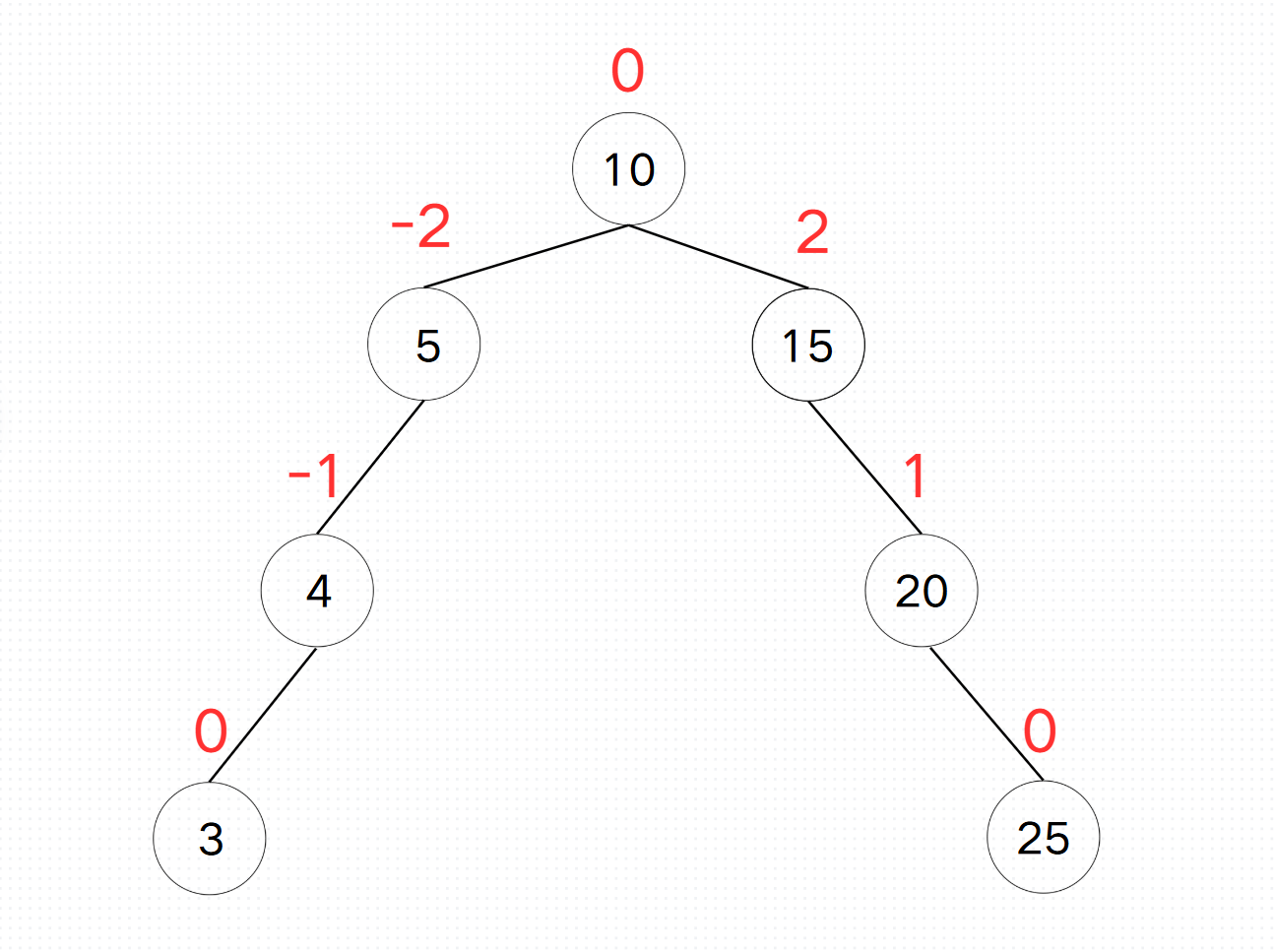
Ⅳ、AVL树节点的设计

我们知道平衡因子是我们判断AVL树是否失衡的标准所以我们要在我们的节点里加入平衡因子( _bf )，如果AVL树失衡的时候要对树进行调整我们需要频繁访问我们的左子树，右子树和节点的父亲节点所以我们要加入左节点的指针(_left) 和 右子树的节点(_right) 。

这里_data类型我们直接写成pair<K,V>类型。

Ⅴ、如何去插入新节点

 一、寻找到合适的节点插入节点

AVL树要符合二叉搜索树的性质，左子树是比节点小的节点而右子树是比节点大的节点，所以AVL树找到合适的位置插的方式与二叉搜索树的方式是一样的。这里相同的值插入不进去，如果想要插入相同的值的话可以把cur->_data.first < data.first 变成cur->_data.first <= data.first

 二、将新节点与AVL树链接在一起

这里要注意的是要判断新节点在parent节点的左节点还是右节点

三、向上调整平衡因子并且调整

插入新节点只会影响到祖先的平衡因子，所以我们要从cur向上寻找parent去调整，最坏的情况是调整到根节点也有可能是只会调整部分的祖先节点。如果调整到最后都没有失衡那就结束，如果失衡了就要进行旋转，旋转的本质是把parent那个节点向低的那个子树压，旋转之后整个子树的高度是不变的所以对这颗子树的祖先的平衡因子不会造成影响。

1、插入不会造成失衡的情况并且向上调整到根：

2、插入不会造成失衡并且向上调整部分祖先：

3、插入向上调整并且会造成旋转：

这种分为很多种情况比如左旋，右旋，左右双旋和右左双旋。旋转的原则是：旋转之后依旧保持二叉搜索树的性质，旋转之后使树从不满足AVL树的性质变成满足AVL树的性质并且降低树的高度。下面我们先从左旋说起

        1、左旋

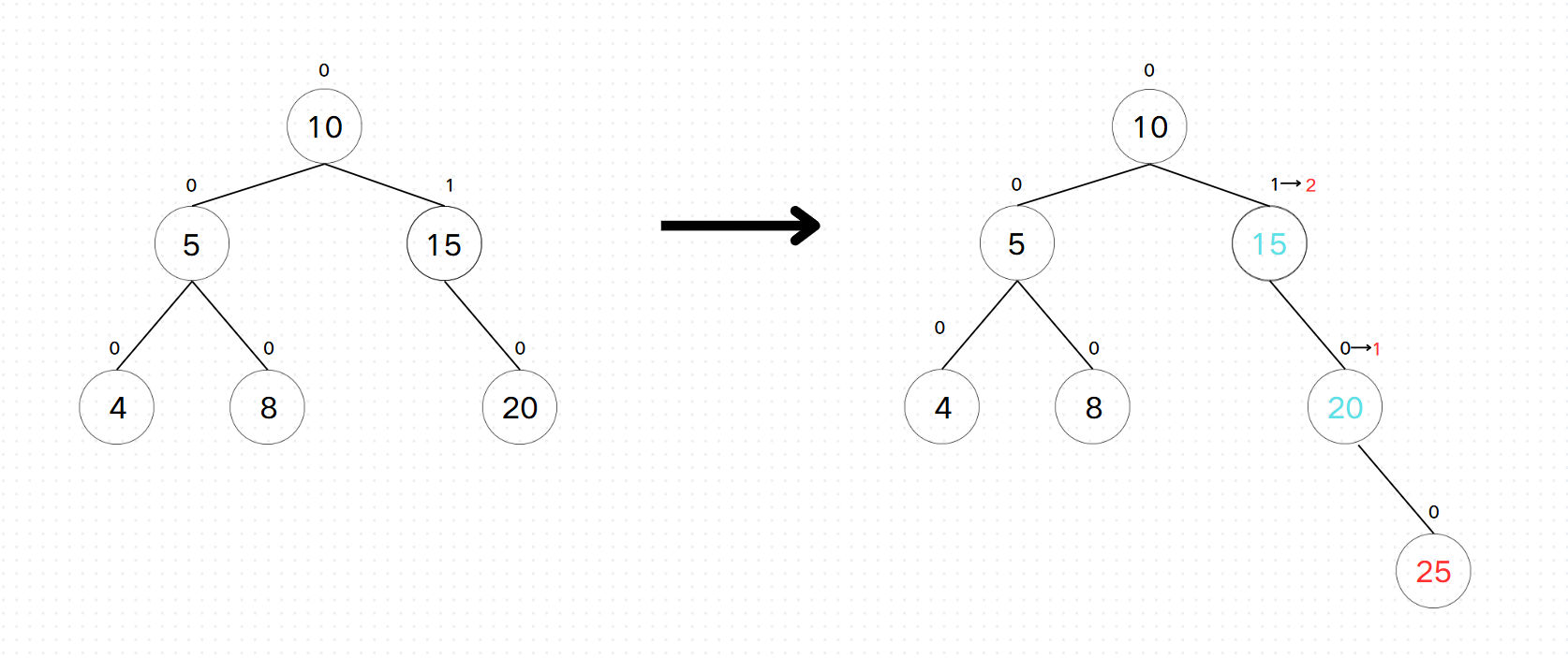
这种情况15节点的平衡因子已经变成了2已经失衡，如何调整才能使重现变成AVL树呢？我们可以把20这个节点作为右子树的父亲节点而15和25分别做他的左子树和右子树，如果要实现这样我们要把20的左子树给15，15变成20的右子树这样既符合二叉搜索树的性质而且这三个节点的平衡因子都不会超过-2 / 2。我们再来看一下抽象图。这里的hb是heightblack的缩写。为了更好的控制我们在这里增加三个参数分别是subR，subRL，parent，pparent 。

用代码怎么去处理这个问题呢？在处理parent->parent ,subL->_parent,subLR->_parent的时候要注意小心形成环和空指针的访问。

void RotateL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
	if (subRL != nullptr)
	{
		subRL->_parent = parent;
	}
	
	parent->_right = subRL;
	Node* pparent = parent->_parent;
	subR->_left = parent;
	parent->_parent = subR;
	if (parent == _root)
	{
		subR->_parent = pparent;
		_root = subR;
	}
	else
	{
		subR->_parent = pparent;
		if (pparent->_left == parent)
		{
			pparent->_left = subR;
		}
		else
		{
			pparent->_right = subR;
		}
	}
	subR->_bf = 0;
	parent->_bf = 0;
}

        2、右旋 

右旋的分析和解决思路和左旋的一样

右旋的注意事项与左旋的一样

void RotateR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	parent->_left = subLR;
	if (subLR != nullptr)
	{
		subLR->_parent = parent;
	}
	
	subL->_right = parent;
	Node* pparent = parent->_parent;
	parent->_parent = subL;
	if (parent == _root)
	{
		_root = subL;
		subL->_parent = pparent;
		
	}
	else
	{
		if (pparent->_left == parent)
		{
			subL->_parent = pparent;
			pparent->_left = subL;
		}
		else
		{
			subL->_parent = pparent;
			pparent->_right = subL;
		}
	}
	subL->_bf = 0;
	parent->_bf = 0;
}

3、左右双旋

上面的图我们可以看见这种parent和subL/subR的平衡因子的符号不相同时单独的左旋和右旋是不能解决问题的旋转出来的结果既不符合二叉搜索树的性质也不符合AVL树的要求。那应该什么办呢？我们可以观察到对于subL/subR来说他们是右子树高/左子树高而对于parent来说他们是左子树高/右子树高正好相反，如果我们把subL/subR旋转一下变成单纯的左高/单纯的右高再进行右旋/左旋这样不就解决问题了。

这样再对图1进行右旋，对图2进行左旋这样就可以解决问题。下面我们分析一下需要左右双旋的情况，下面我们抽象一下

在经过左右双旋以后会变成下面这幅图这样

void RotateLR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	 
	int bf = subLR->_bf;
	RotateL(parent->_left);
	RotateR(parent);
	
	if (bf == -1)
	{
		parent->_bf = 1;
		subL->_bf = 0;
		subLR->_bf = 0;
	}
	else if(bf ==1)
	{
		parent->_bf = 0;
		subL->_bf = -1;
		subLR->_bf = 0;
	}
	else if (bf == 0)
	{
		subLR->_bf = 0;
		subL->_bf = 0;
		parent->_bf = 0;
	}
	else
	{
		cout<<"左右双旋出现问题" << endl;
		assert(false);
	}
}

我们细细观察b这个子树12这个节点的平衡因子不同也代表了最后结果的10和15节点的平衡因子不一样。从最开始的树到最后的结果我们可以看见12节点的左子树给了10做右子树而12节点的右子树给15做了左子树，所以新节点插入在12节点的左子树还是右子树有很大的区别。还有一点再次强调一下因为旋转的本质是把根节点向高度低的子树压，从而可以降低整个树的高度使得左右子树的高度相同。从这我们也知道parent旋转之后的平衡因子都是0无论是左，右单旋还左右，右左双旋，节点的平衡因子0 时对他的祖先造不成影响所以不在需要向上调整所以在需旋转完了以后要break。

4、右左双旋

右左双旋的分析思路与左右双旋相同，可以看上面的分析理解。

void RotateRL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;

	int bf = subRL->_bf;

	RotateR(parent->_right);
	RotateL(parent);
	
	if (bf == -1)
	{
		subR->_bf = 1;
		subRL->_bf = 0;
		parent->_bf = 0;
	}
	else if (bf == 1)
	{
		subRL->_bf = 0;
		parent->_bf = -1;
		subR->_bf = 0;
	}
	else if(bf == 0)
	{
		subRL->_bf = 0;
		subR->_bf = 0;
		parent->_bf = 0;
	}
	else
	{
		cout << "右左双旋出现问题" << endl;
		assert(false);
	}
}

Ⅵ、总结

ALV树是一颗二叉搜索平衡树，AVL树的出现可以很好的避免出现二叉搜索树出现单枝的情况出现保证了效率不会出现很大的下降，他的性质是左右子树都是AVL树，左右子树的高度差不高于+1/-1。

当插入新节点的时候寻找合适位置的方式与二叉搜索树的方法是一样的（这里要注意新节点要与整个树要连接），插入以后要以向上更新parent的平衡因子如果出现了 -2 / +2的情况要进行调整。调整分为四个情况分别是左旋，右旋，左右双旋，右左双旋。两个单旋对应的情况是parent与subL/subR的平衡因子符号相同的情况，而两个双旋的情况是parent与subL/subR的平衡因子符号不相同的情况，这样的解决办法是把他变成一边高这种单纯的样子再去使用单旋去解决问题。

旋转的本质我认为就是将根节点向比较低的子树去压这样能降低高的子树的高度又能提高低的子树的高度，从而达成左右子树平衡的效果这使得这颗AVL树可以保持自己的性质不变。

当然对于节点的设计我们也可以不加入平衡因子去进行判断这颗AVL树是否出问题。