1 为什么要引入逻辑回归
前面用的是线性回归对数据进行预测,那么这门简单的模型能预测一切数据吗,答案肯定是不能,今天就要引入另一个比较常用的模型,逻辑回归模型。下面我们看一个简单的案例解释为什么需要逻辑回归模型,如果以某人是否会选择去看电影为例,先给出数据:
qian=[[-4,-3,-2,-1,0,1,2,3,4]]
kan=[[0,0,0,0,0,1,1,1,1]]
qian分别表示他的钱数,kan表示对应的钱数是否去看电影,0表示不去,1表示去。用前面的线性回归分析得到如下图形和数据,代码数据如下:

代码:
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
import random
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,r2_score
qian=range(-4,5,1)
qian=np.array(qian)
kan=[0,0,0,0,0,1,1,1,1]
kan=np.array(kan)
print(qian,kan)
qian=qian.reshape(-1,1)
kan=kan.reshape(-1,1)
lr_regression=LinearRegression()
lr_regression.fit(qian,kan)
kan_yuce=lr_regression.predict(qian)
plt.scatter(qian,kan,color="red")
plt.scatter(qian,kan_yuce,color="blue")
plt.show()
注意预测数据是一条直线,与我们说的大于0.5表示去,小于0.5表示不去看电影有点不符合,对代码进行修正如下
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
import random
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,r2_score
qian=range(-4,5,1)
qian=np.array(qian)
kan=[0,0,0,0,0,1,1,1,1]
kan=np.array(kan)
print(qian,kan)
qian=qian.reshape(-1,1)
kan=kan.reshape(-1,1)
lr_regression=LinearRegression()
lr_regression.fit(qian,kan)
kan_yuce=lr_regression.predict(qian)
#进行修正预测
kan_yuce_xiuzheng=[]
for element in kan_yuce:
if element<0.5:
kan_yuce_xiuzheng.append(0)
else:
kan_yuce_xiuzheng.append(1)
plt.scatter(qian,kan,color="red")
plt.scatter(qian,kan_yuce,color="blue")
plt.scatter(qian,kan_yuce_xiuzheng,color="#ff00ff")
print(kan_yuce,kan_yuce_xiuzheng)
plt.show()
得到的图形如下:

注意图中打印出来的数据,对应图表中的是预测的紫色点覆盖了原来红色的实际数据。这个比较好的进行了数据预测。那为什么还要引入逻辑回归呢?在代码中加入一个比较大的数据,如收入1000,此时对应的代码:
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
import random
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,r2_score
qian=list(range(-4,5,1))
kan=[0,0,0,0,0,1,1,1,1]
qian.append(1000)
kan.append(1)
kan=np.array(kan)
qian=np.array(qian)
print(qian,kan)
qian=qian.reshape(-1,1)
kan=kan.reshape(-1,1)
lr_regression=LinearRegression()
lr_regression.fit(qian,kan)
kan_yuce=lr_regression.predict(qian)
#进行修正预测
kan_yuce_xiuzheng=[]
for element in kan_yuce:
if element<0.5:
kan_yuce_xiuzheng.append(0)
else:
kan_yuce_xiuzheng.append(1)
plt.scatter(qian,kan,color="red")
plt.scatter(qian,kan_yuce,color="blue")
plt.scatter(qian,kan_yuce_xiuzheng,color="#ff00ff")
print(kan_yuce,kan_yuce_xiuzheng)
plt.show()
请实际运行看实际得到的数据如下:

从数据中可以看出,如果有数据差别比较大的时候则模型不能预测正确的结果。这也是线性回归模型不能实现的,接下来我们使用可以解决问题的逻辑模型。
2 什么是逻辑模型
logistic回归又称logistic回归分析,是一种广义的线性回归分析模型,常用于数据挖掘,疾病自动诊断,经济预测等领域。 逻辑回归根据给定的自变量数据集来估计事件的发生概率,由于结果是一个概率,因此因变量的范围在 0 和 1 之间。例如,探讨引发疾病的危险因素,并根据危险因素预测疾病发生的概率等。Logistic回归是一种广义线性回归(generalized linear model),因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同,都具有 w‘x+b,其中w和b是待求参数,其区别在于他们的因变量不同,多重线性回归直接将w‘x+b作为因变量,即y =w‘x+b,而logistic回归则通过函数L将w‘x+b对应一个隐状态p,p =L(w‘x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数,就是logistic回归,如果L是多项式函数就是多项式回归。logistic回归的因变量可以是二分类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释,多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归。
逻辑回归模型通常使用sigmoid函数,注意sigmoid函数,sigmoid时S型的意思,所以它不止一个函数。最常用的p(x)=其图形如下:
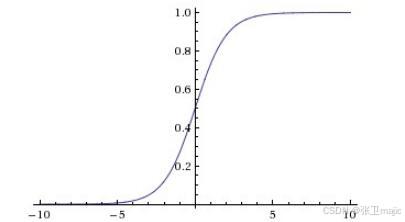
另外还有其他的sigmoid函数如下图所示:
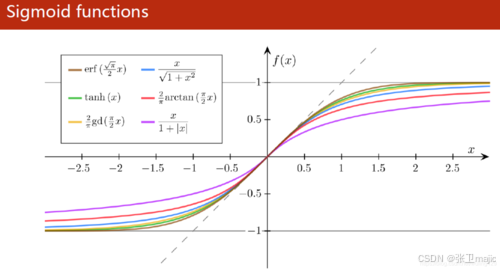
其中p (x)=比较典型的一个特点就是x=0时f(0)=1/2,所以经常可以将其值大于0.5划分为一类,小于0.5划分为另一类,这也是为什么说逻辑回归更容易做二分类的问题。在此-x在一些复杂的问题中可以用-g(x)来表示,从而解决更复杂的问题。此处一定注意思考清楚为什么,不然理工科会更严谨的论证孔子老先生讲的“学而不思则罔,死而不学则die”。思考吧。。。。
思考清楚后再看下来,那问题是以后的求解就需要求出这个g(x),如何求出这个g(x)才是最重要的。有点像线性回归确定其系数,也是要将其损失函数达到最小,线性回归函数中
而在逻辑回归中标签和结果可能都是离散的点,而离散的点是无法求导从而无法用梯度下降寻找最小值。怎么办呢?知识是智慧的结晶,需要传承,也就是要站在前人经验的基础上才能够的更高。
这个经验公式以yi=0时分析为例,p(xi)充当自变量,此时需要鼓励p(xi)<0.5的情况,需要使损失函数小,而当p(xi) >0.5时扩大损失函数。yi=1时相反。请结合函数的图形:
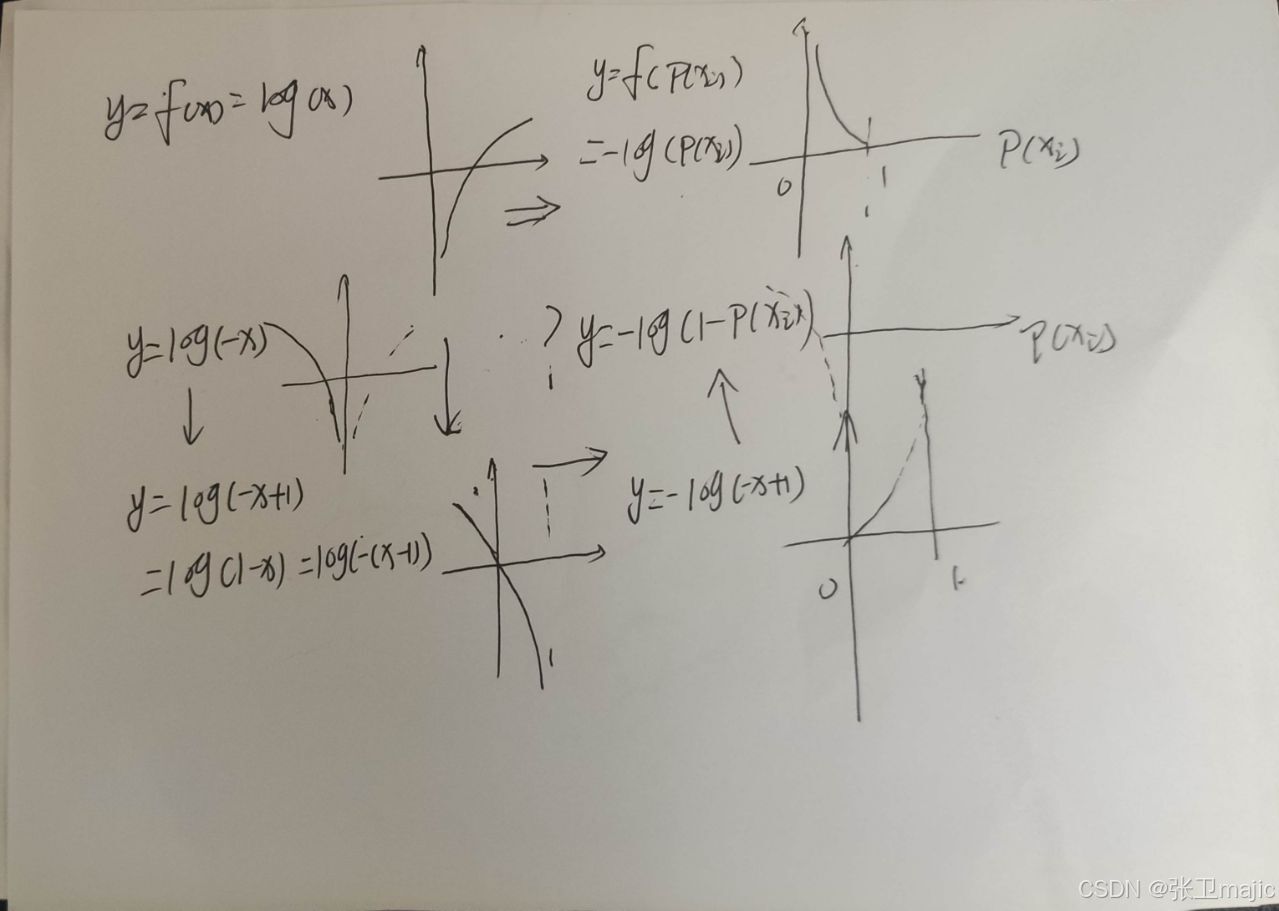
这样做是将原来离散的值变成了连续的值,从而得到逻辑回归函数的损失函数为
其中
p (x)=
然后再利用梯度下降法求最优参数即可。这些内容如果有问题需要温习数学基本知识,他们构成我们理解算法的知识基础,在此不叙。
3 使用逻辑回归的步骤
我们看一下使用scikit-learn如何进行逻辑回归分析:
主要步骤有:
1)引入模型 from sklearn.linear_model import LogisticRegression
2) 产生逻辑回归模型对象 lr_model=LlgisticRegression()
3) 训练模型 lr_model.fit(x,y)
4)边界函数即上面提及的g(x)的各个系数
theta1,theta2=LR.coef_[0][0],LR.coef_[0][1], theta0=LR.intercept_[0]...
5) 基于模型进行预测
data_predictions=lr_model.predict(x_new)
6)模型的评估 Accuracy=正确预测样本数量/总样本数量,使用模块中对应的包即可计算。import accuracy_score.
accuracy=accuracy_score(y,y_predictions)
这个结果可以通过实际图形给出直观模拟!
本次博文主要分享逻辑回归的用途和原理,下次计划进行一次实际使用,感谢关注,成长的路上一起加油努力!
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








