Part 5 DFS和BFS搜索

原创已于 2025-02-13 19:42:02 修改 · 1.6k 阅读

40 ·

CC 4.0 BY-SA版权

文章标签：

#深度优先 #宽度优先 #算法

于 2025-02-13 19:41:15 首次发布

一、优先搜索

（1）深度优先搜索（DFS）

深度优先搜索可以理解为走迷宫的试错，向一个方向走到底并记下路上出现的所有分支点，如果尽头是死路，就回到上一级分支点，向另一个方向试错，直到找到出口，或将该分支点的所有可能性探测完并返回再上一级的分支点

伪代码：

dfs(起点（第一分支点）){
    if(满足条件){  //终止循环
        返回终点数值;
    }
    起点标记为走过;  //防止走回头路，死循环
    起点开拓出下一步（下一步n种可能）;
    for(int i=0;i<n;i++)
        if(下一步i合理){
            dfs(下一步);  //递归
        }
        回溯;  //清除search(下一步)的影响，返回原状态
    }
}

（2）广度优先搜索（BFS）

广度优先搜索就是在走迷宫的基础上，外加要求：找到最快捷的路线。那么仅仅是从某一步向下深挖直到找到出口是不能进行步数比较的，所以不妨对每一个方向的路线同时进行探索，储存，先找到出口的就是最快路线

伪代码：

bfs(起点){
    queue<int> que;  //假设方向记为整数,并为将要进行的搜索过程量建立队列
    que.push(起点)；
    起点标记为走过； //防止走回头路
    数据初始化;
    while(!q.empty()){  //队列que未空，则每一种可能性还未探索结束
        记录数值;
        该点=que.front()  //从队首找到将要处理的位置，也能保证同时性
        该点开拓出下一步（n种）;
        for(int i=0;i<n;i++){
            if(下一步合理){
                que.push(下一步的位置);
            }
        }
        q.pop();  //清除已经探索过的路径，因为不会回溯了
    }
    返回终点数值;
}

详细模板请看：第十三章 DFS与BFS（保姆级教学！！超级详细的图示！！）_dfs bfs-CSDN博客

好，直接上例题！

二、专题训练

（1）自然数的拆分问题

题目：P2404 自然数的拆分问题 - 洛谷

仔细看看，如果把第i个拆分出来的数看作分支点，接下来的可能一个个向下探索，在保证每个数字的右侧一定比它大，这和深搜的逻辑完全合理（而且满足按字典序排列的要求），袜，严丝合缝！

#include<bits/stdc++.h>
using namespace std;
int n;
vector<int> assign;
void dfs(int now,int sum){
    if(sum==n){
        int i=0;
        for(auto x:assign){
            if(i) cout<<"+";
            cout<<x;
            i++;
        }
        cout<<endl;
    }
    for(int i=now;i<n;i++){
        if(sum+i<=n){
            assign.push_back(i);
            dfs(i,sum+i);
            assign.pop_back();
        }
    }
}
int main(){
    cin>>n;
    dfs(1,0);
    return 0;
}

（2）填涂颜色

题目：P1162 填涂颜色 - 洛谷

一看题目好像多了个只改变“1”圈内的0，搜寻这种0反而不方便，反过来想，删除边界上的0，保证在给所有0改2时不该变边界上的0，就可以解决了。这里是典型的连接块问题，不论是dfs还是bfs都能遍历边界上的0块，这里使用dfs：

#include<bits/stdc++.h>
using namespace std;
int square[30][30],dtx[4]={-1,1,0,0},dty[4]={0,0,-1,1};  //方向数组
int n;
bool bs[30][30];
void paint(int x,int y){  //为0块涂保护色
    if(x<0||y<0||x>=n||y>=n||square[x][y]==1||bs[x][y]){
        return;
    }
    bs[x][y]=true;
    for(int i=0;i<4;i++){
        paint(x+dtx[i],y+dty[i]);
    }
}
void search(){  //边界0块处理
    for(int i=0;i<n;i++){
        if(square[0][i]==0&&!bs[0][i]) paint(0,i);
    }
    for(int i=0;i<n;i++){
        if(square[i][0]==0&&!bs[i][0]) paint(i,0);
    }
    for(int i=0;i<n;i++){
        if(square[i][n-1]==0&&!bs[i][n-1]) paint(i,n-1);
    }
    for(int i=0;i<n;i++){
        if(square[n-1][i]==0&&!bs[n-1][i]) paint(n-1,i);
    }
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            cin>>square[i][j];
            bs[i][j]=false;
        }
    }
    search();
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            if(square[i][j]==0&&!bs[i][j]) cout<<2<<" ";
            else cout<<square[i][j]<<" ";
        }
        cout<<endl;
    }
    return 0;
}

（3）显示图像

题目：P1256 显示图像 - 洛谷

由题目可知，黑块到任意白块的曼哈顿距离的最小值即为该黑块到白块的最小距离，如果将样例的数值以颜色替代：

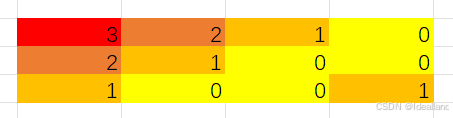
就会发现，相邻的黑块最小距离差1，而且距离白块越远，颜色越深，数值越大；

猜想：如果从白块出发，每到一个黑块就记录下行动的格数，只记录先到的（最近），就会发现和图片相符；

那么，这题是不是模拟这个过程，就可以得到答案了？

确实：利用广搜，默认白块的距离为一，递推每个白块到每个黑块的最小步数的最小值，将相应的值赋给对应位置即可：

#include<bits/stdc++.h>
using namespace std;
const int NMAX=1e6;
struct{
    int x,y;
}que[NMAX];
int head=0,tail=0,n,m;
int dtx[4]={1,-1,0,0},dty[4]={0,0,1,-1};
int dis[200][200];
char pic[200][200];
bool vis[200][200];
void readin(){
    for(int i=0;i<n;i++){
        cin>>pic[i];
        for(int j=0;j<m;j++){
            if(pic[i][j]=='1'){
                tail++;
                que[tail].x=i;que[tail].y=j;
                vis[i][j]=true;
                dis[i][j]=0;
            }else{
                vis[i][j]=false;
            }
        }
    }
}
void bfs(){
    while(head<=tail){
        head++;
        for(int i=0;i<4;i++){
            int xa=que[head].x+dtx[i],ya=que[head].y+dty[i];
            if(xa>=0&&ya>=0&&xa<n&&ya<m&&!vis[xa][ya]){
                vis[xa][ya]=true;
                tail++;
                que[tail].x=xa;que[tail].y=ya;
                dis[xa][ya]=dis[que[head].x][que[head].y]+1;
            }
        }
    }
}
int main(){
    cin>>n>>m;
    readin();
    bfs();
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            cout<<dis[i][j]<<" ";
        }
        cout<<endl;
    }
    return 0;
}

（4）健康的荷斯坦奶牛 Healthy Holsteins

题目：P1460 [USACO2.1] 健康的荷斯坦奶牛 Healthy Holsteins - 洛谷

这里和例题（1）原理是相同的，根据每种饲料，对每种使用的情况深搜，从饲料1向下递推。不同在每次得出合理搭配时需要返回去和先前的搭配比较使用的饲料种数，取少且字典序优先的：

#include<bits/stdc++.h>
using namespace std;
int v,g,minans;
int nutrition[30][30],needs[30],sum[30];
vector<int> ans;
vector<int> trail;
void dfs(int x){
    if(trail.size()>=minans) return;
    bool b=true;
    for(int i=0;i<v;i++){
        if(sum[i]<needs[i]){
            b=false;
            break;
        }
    }
    if(b){
        if(trail.size()<minans){
            minans=trail.size();
            ans=trail;
            return;
        }
    }
    for(int i=x;i<g;i++){
        for(int j=0;j<v;j++){
            sum[j]+=nutrition[i][j];
        }
        trail.push_back(i+1);
        dfs(i+1);
        for(int j=0;j<v;j++){
            sum[j]-=nutrition[i][j];
        }
        trail.pop_back();
    }
}
int main(){
    cin>>v;
    for(int i=0;i<v;i++){
        cin>>needs[i];
    }
    cin>>g;
    minans=g+1;
    for(int i=0;i<g;i++){
        for(int j=0;j<v;j++){
            cin>>nutrition[i][j];
        }
    }
    dfs(0);
    cout<<ans.size()<<" ";
    for(auto i:ans){
        cout<<i<<" ";
    }
    cout<<endl;
    return 0;
}

（5）GRZ-Ridges and Valleys

题目：P3456 [POI 2007] GRZ-Ridges and Valleys - 洛谷

这题也是连接块的问题，关键在于判断某块是山峰还是山谷；

核心：搜索（遍历），找到与某点相连的块（方向数组拓展），判断是否是山峰以及山谷（边界）（注意：拓展方向有八个，超平坦地图被视为单山峰兼单山谷，以及存在非峰非谷地区）

这里可以使用深搜，也可以使用广搜，但是深搜TLE的几率大的离谱，除了在题解的一位大佬写的深搜，我真心找不到时间能过的深搜写法，所以还是用广搜吧：

#include<bits/stdc++.h>
using namespace std;
int n,npeak=0,nvalley=0;
int mapp[1000][1000];
bool mappp[1000][1000];
int dtx[8]={-1,1,0,0,-1,1,-1,1},dty[8]={0,0,-1,1,-1,-1,1,1};
void bfs(int x,int y){
    queue<pair<int,int>> que;
    que.push({x,y});
    mappp[x][y]=true;
    bool b1=true,b2=true;
    while(!que.empty()){
        auto [nx,ny]=que.front();
        que.pop();
        for(int i=0;i<8;i++){
            int tx=nx+dtx[i],ty=ny+dty[i];
            if(tx>=0&&ty>=0&&tx<n&&ty<n){
                if(mapp[tx][ty]>mapp[nx][ny]) b1=false;
                if(mapp[tx][ty]<mapp[nx][ny]) b2=false;
                if(mapp[tx][ty]==mapp[nx][ny]&&!mappp[tx][ty]){
                    mappp[tx][ty]=true;
                    que.push({tx,ty});
                }
            }
        }
    }
    if(b1) npeak++;
    if(b2) nvalley++;
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            cin>>mapp[i][j];
            mappp[i][j]=false;
        }
    }
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            if(!mappp[i][j]) bfs(i,j);
        }
    }
    cout<<npeak<<" "<<nvalley<<endl;
    return 0;
}

（6）八皇后 Checker Challenge

题目：P1219 [USACO1.5] 八皇后 Checker Challenge - 洛谷

这就是典型的深搜模板运用，假设第一颗棋子在某处，对该种情况向下一颗棋子深搜，排除不合理的可能，将答案存入结果；

关键在合理的判断：

（1）不能在同一行：只要一行放一颗（只考虑一颗）即可；

（2）不能在同一列：设置数组y，将每颗棋子横坐标对应的数组位置标记，防止其他棋子落在相同位置；

（3）不能在同一对角线及其平行线上：对于主对角线，每一条对角线及其平行线上的横纵坐标差值为不同的定值；而副对角线及其平行线上横纵坐标之和为不同的定值，则设置两个数组dll和dlr，分别标记每颗棋子对应位置即可；

综上：

#include<bits/stdc++.h>
using namespace std;
int n;
int y[14],dll[27],dlr[27];
vector<vector<int>> ans;
vector<int> posi;
void dfs(int k){
    if(k>n){
        ans.push_back(posi);
        return;
    }
    for(int i=1;i<=n;i++){
        if(!y[i]&&!dll[i+k]&&!dlr[n+k-i]){
            posi.push_back(i);
            y[i]++;dll[i+k]++;dlr[n+k-i]++;
            dfs(k+1);
            posi.pop_back();
            y[i]--;dll[i+k]--;dlr[n+k-i]--;
        }
    }
}
int main(){
    cin>>n;
    dfs(1);
    for(int i=0;i<3;i++){
        for(auto x:ans[i]){
            cout<<x<<" ";
        }
        cout<<endl;
    }
    cout<<ans.size()<<endl;
    return 0;
}