1008制衡
题目、输入、输出:
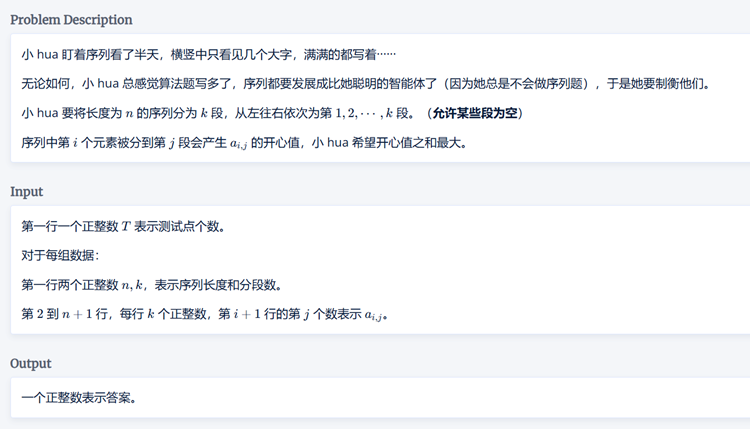
样例:

大致题意:每组输入是n行k列的,我们每一行只能选择一个,而且每行选择的那个数所在的列位置,要在所有行选择的列位置呈现单调递增,输出每行选择的数加起来最大。
思路:DP
定义:f[ i ] [ j ] : 前i 行 前j 列能取得的最大总和数
初始化:动态规划数组全置0
转移方程:f[ i ] [ j ]=max(f[ i-1 ] [ j ]+v [ i ][ j ] , f[ i ][ j-1 ]) : 在拿当前数,不拿当前数直接拿前一列当前行最大总和数中,取max。
代码:
#include <bits/stdc++.h>
using namespace std;
int main(){
int T;
cin >> T;
int n,m;
while(T--){
cin >> n >> m;
vector<vector<int>> v(n+2,vector<int>(m+2)); //输入数组
vector<vector<int>> f(n+2,vector<int>(m+2)); //动态规划数组
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++) {
cin >> v[i][j];
//转移方程
f[i][j]=max(f[i-1][j]+v[i][j],f[i][j-1]) ;
}
}
cout << f[n][m]<<'\n';
}
return 0;
}
1005持家
题目、输入、输出:

样例:

大致题意: 每组测试样例给出商品价格p,n张优惠卷,最多能使用的优惠卷数列k,每张优惠卷给出两个数a,b;a=0:表示打b折,a=1:表示减去b元,输出商品使用优惠卷后的最低价格。
思路:排序+前缀和+枚举
将打折的存到t0数组,从小到打排序,减价的存到t1数组,从大到小排序,t1数组的前缀和存到q数组,因为如果要打折的话,肯定直接在最前面使用打折卷,直接枚举拿t0的个数,得到k-i个t1的个数,ans取min即可,最后ans要特判一下不能<0。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int t0[N],t1[N],q[N];
int main(){
int T;
cin >> T;
int p,n,k,a,b;
t0[0]=10; //初始化:打折卷拿0张的时候,p*t[0]*0.1
while(T--){
cin >> p >> n >> k;
int cnt0=1,cnt1=1;
while(n--){
cin >> a >> b;
if(a==0) t0[cnt0++]=b;
else t1[cnt1++]=b;
}
sort(t0+1,t0+cnt0); //排序
sort(t1+1,t1+cnt1,greater<int>());
for(int i=1;i<cnt1;i++) q[i]=q[i-1]+t1[i]; //t1前缀和
double ans=1e9,sum=p;
for(int i=0;i<=k&&i<cnt0;i++){
sum*=0.1*t0[i];
ans=min(ans,sum-q[k-i]);
}
if(ans<0) ans=0;
printf("%.2lf\n",ans);
}
return 0;
}
1006进步
题目、输入、输出:

样例:

大致题意: 每组测试样例给出n个数,m次操作,有两种操作方式,输入x,l,r:x=1:将l位置的值改成r,x=2:为 ⌊前r个数总和/100⌋−⌊前l-1个数的总和/100⌋。(向 0 取整,即 ⌊−101/100⌋=−1),第i个操作2的答案:ansi,最后输出答案ans^=ansi*i
思路:树状数组
板题,直接套树状数组模板,处理一下ans计算即可。
代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+10;
int t[N],p[N]; //t:原数组,p:树状数组
int n,m;
int lo(int x){ //树状数组
return x&-x;
}
void add(int x,int d){
while(x<=n){
p[x]+=d;
x+=lo(x);
}
}
int sum(int x){
int res=0;
while(x){
res+=p[x];
x-=lo(x);
}
return res;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
int T;
cin >> T;
while(T--){
cin >> n >> m;
for(int i=1;i<=n;i++) p[i]=0; //初始化
for(int i=1;i<=n;i++) {
cin >> t[i];
add(i,t[i]);
}
int x,l,r,cnt=1,ans=0;
while(m--){
cin >> x >> l >> r;
if(x==1){
add(l,-t[l]); //减去原来
t[l]=r;
add(l,r); //加上选择
}
else {
int d=(sum(r)/100-sum(l-1)/100);
ans^=(d*cnt++);
}
}
cout << ans <<'\n';
}
return 0;
}
1001战斗爽
题目、输入、输出:

样例:
输入:
5
6 4 2 68
4 4
4 13
2 13
5 17
6 9
19 17
3 21 2 48
4 7
6 5
8 20
6 12 7 54
4 4
5 19
2 1
3 12
7 5
16 2
6 4 3 68
4 4
4 13
2 13
5 17
6 9
19 17
3 21 51 48
4 7
6 5
8 20
输出:
1
3
6
1
3
对于所有数据:1≤T≤100, 1≤n≤1e4, 1≤u,hq,ai,hi≤1e9, 1≤k≤1e3
大致题意: 每组测试样例输出n个敌人,小hua的攻击力u,敌人最多受到攻击的次数k,小hua初始的血量hq,接着n行给出每个敌人的攻击力和初始血量。
小hua每个回合攻击敌人遵循:攻击一个受到伤害不足 k次的存活的敌人(若有多个则攻击剩余血量最低的一个,若仍有多个则攻击攻击力最低的一个,若还有多个则攻击编号最小的一个),若当前敌人从未受过攻击,则它受到 u 点伤害,否则受到 ⌊u/2⌋点伤害,血量为0则为死亡;
而小hua每个回合受到的攻击是当前存活敌人的最大攻击值,问战斗结束时小 hua 共击杀了多少个敌人。
思路:模拟
用优先队列q按照血量,攻击力,编号从小到大存敌人的信息,再用优先队列qma按攻击力,编号从大到小存敌人信息,用map<int,int>mp存此编号敌人是否被杀,来判断攻击力是否更新,在小hua没有死亡前遍历q,进行判断看是否能击杀当前敌人,可以则ans++,当小hua血量<=0时退出循环。
代码:
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
typedef pair<int,int> PII; //攻击,编号
typedef array<int,3> ar3; //血量,攻击,编号
map<int,int>mp; //标记是否被杀
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
int T;
cin >> T;
while(T--){
int n,u,k,hq;
cin >> n >> u >> k >> hq;
priority_queue<ar3,vector<ar3>,greater<ar3>> q;
priority_queue<PII> qma;
mp.clear();
ar3 ar;
PII pi;
for(int i=1;i<=n;i++){
cin >> ar[1]>>ar[0]; //题目先输入攻击,后输入血量
ar[2]=i,pi.fi=ar[1],pi.se=i;
q.push(ar);
qma.push(pi);
}
int ma=qma.top().fi , s=qma.top().se;
qma.pop();
int ans=0;
while(q.size()){
ar3 x=q.top();
q.pop();
int cnt=(x[0]-u+u/2-1)/(u/2)+1; //杀死敌人最少次数
if(cnt>k){
hq-=k*ma;
if(hq<=0) break;
}
else {
//先手,在敌人最后一次攻击前 已经杀死敌人
hq-=(cnt-1)*ma;
if(hq<=0) break;
mp[x[2]]=1;
if(s==x[2])
while(qma.size()){
pi=qma.top();
qma.pop();
if(!mp[pi.se]){
ma=pi.fi,s=pi.se;
break;
}
}
ans++;
hq-=ma;
if(hq<=0) break;
}
}
cout << ans <<'\n';
}
return 0;
}
1003洞察
题目、输入、输出:

样例:

大致题意:
给定四个整数 k, b, c, v,求满足以下条件的非负整数 x 的个数:
(k·x + b) ^ c = v
思路:二进制+二分+动态区间
逐位处理:从高位到低位依次确定每位取值
二分查找:快速定位满足位条件的最大x值
动态区间维护:通过位条件不断缩小解的范围
通过从高位到低位逐位分析 v的二进制位,确定 k⋅x+b 的对应二进制位应满足的条件,并利用二分法动态维护解的区间范围。

代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
int k,b,c,v;
// 在区间 [l, r] 中找到最大的 r,使得 k*r + b 的第 x 位二进制为 0
int find(int x,int l,int r){
while(l<r){
int mid=l+r+1>>1;
int u=k*mid+b;
if(((u>>x)&1)==0) l=mid;
else r=mid-1;
}
return r;
}
signed main(){
int T;
cin >> T;
while(T--){
cin >> k >> b >> c >> v;
//longlong 最大不溢出: (1LL << 62) - 1,
//不能直接1e18(double)
int ans=0,l=0,r=((1LL << 62) - 1 - b) / k;
// 从高位到低位逐位处理,确保二分的出来的第i位二进制为0的数在当前范围内最大
for(int i=62; i>=0 && l<=r ;i--){
int d=find(i,l-1,r); // d :[l-1, r] 内 k*d + b 的第 i 位为 0最大
//l-1:find 在无解时(没有找到二进制第i位为0的数)返回 l-1
if((v>>i)&1){ //v第i位二进制 为1
if((c>>i)&1){ //c第i位二进制 为1
ans+=r-d; //(d,r]范围的数 第i位二进制 都为1,1((d,r])^1(c)=0<1(v) 符合(kx+b)^c<v
r=d; //大于 m 的 x 已经统计过了
}
else {
ans+=d-l+1; //[l,d]范围的数 第i位二进制 都为0,0([l,d])^0(c)=0<1(v) 符合(kx+b)^c<v
l=d+1; //小于等于 m 的 x 已经统计过了
}
}
else {
if((c>>i)&1){
l=d+1; //[l,d]范围的数 第i位二进制 都为0,0^1(c)=1>0(v),不符合条件,更新l
}
else r=d; //(d,r]范围的数 第i位二进制 都为1,1^0(c)=1>0(v),不符合条件,更新r
}
}
if(l<=r) //处理剩余区间
ans+=r-l+1;
cout << ans <<'\n';
}
return 0;
}
2025“钉耙编程”中国大学生算法设计春季联赛(2)题解链接:
HDU 2025“钉耙编程”中国大学生算法设计春季联赛(2)(补题)-CSDN博客
2025“钉耙编程”中国大学生算法设计春季联赛(3)题解链接:
2025“钉耙编程”中国大学生算法设计春季联赛(3)(补题)-CSDN博客
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








