蓝桥杯-ALGO-2 最大最小公倍数
如果按照一般的方法来做的话,不用想,绝对会超时。
举个例子
当n为奇数时 比如为7 那么其在1-7中选取三个数的最大最小公倍数为7*6*5
即是MAX = n * (n-1) * (n-2)
因为当三个数互质且连续的时候,其最大公约数不超过2,也就是1,所以为三个数的乘积。当n为偶数的时候,比如为8,那么n-2就是偶数,也就是不满足那个定律,那么我们可以向后退一位,
即是MAX = n * (n-1) * (n-3)
那么n-3就满足定律了-接下来最后一点,当n为3的倍数的时候,if (n % 3 == 0) 比如为6
我们可能会想到n-3、n-4都不管用、那么我们可以把n往后退一位
即是MAX = (n-1) * (n-2) * (n-3)
代码如下:
#include<cstdio>
#include<iostream>
using namespace std;
long long N;
int main() {
long long ans;
scanf("%d", &N);
if (N <= 2) {
ans = N;
}
else if(N % 2) {
ans = N*(N-1)*(N-2);
}
else {
if (N % 3) {
ans = N*(N-1)*(N-3);
}
else ans = (N-1)*(N-2)*(N-3);
}
cout << ans << endl;
return 0;
}结果如下:
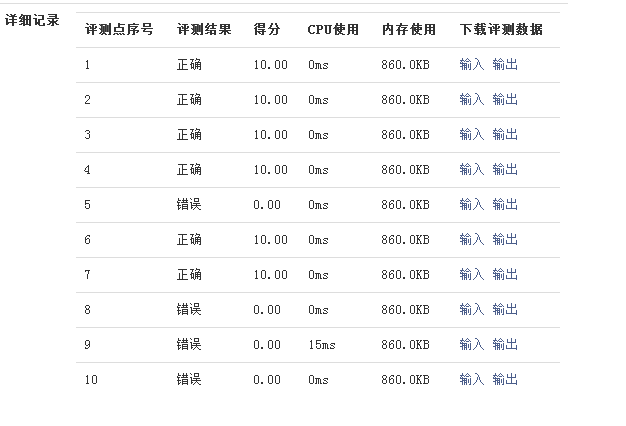
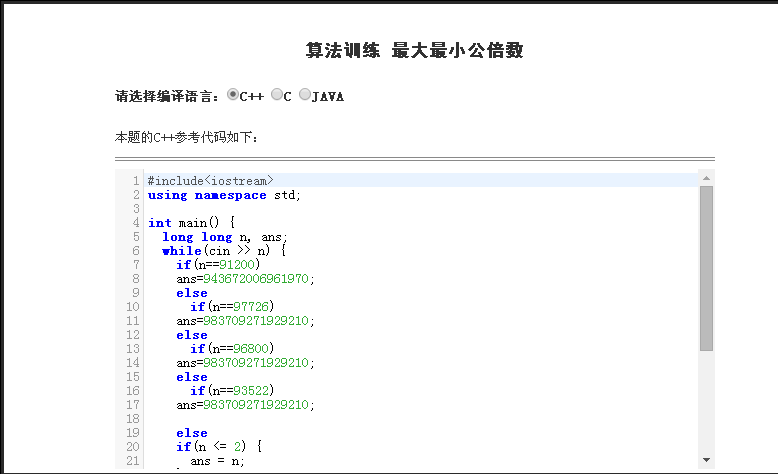
我看了那组数据(博主是VIP)
91200
943672006961970
再来一张图片
我也是醉了 ….. 数据有误 如果不写if…else估计他自己也过不了…
所以是数据有误 别担心
2015年9月15日12:31:21
























 221
221

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








