高斯消元基础题

最新推荐文章于 2024-05-03 19:20:28 发布
最新推荐文章于 2024-05-03 19:20:28 发布
阅读量4.1k 收藏 5
点赞数 2
分类专栏： 基础数学
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/ACdreamers/article/details/8997459
版权

题目：http://poj.org/problem?id=1222

 

题意：5*6矩阵中有30个灯，操作一个灯，周围的上下左右四个灯会发生相应变化 即由灭变亮，由亮变灭，如何操

     作使灯全灭？

 

分析：这个问题是很经典的高斯消元问题。同一个按钮最多只能被按一次，因为按两次跟没有按是一样的效果。那么

     对于每一个灯，用1表示按，0表示没有按，那么每个灯的状态的取值只能是0或1。列出30个方程，30个变

     元，高斯消元解出即可，因为解只能是0或者1，所以方程组是一定有解。

 

代码：

#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
#include <math.h>

using namespace std;
const int N = 35;

int gcd(int a,int b)
{
    return b ? gcd(b,a%b):a;
}

int lcm(int a,int b)
{
    return a / gcd(a,b) * b;
}

void Gauss(int a[][N],int n,int m,int &r,int &c)
{
    r = c = 0;
    for(; r<n && c<m; r++,c++)
    {
        int maxi = r;
        for(int i=r+1; i<n; i++)
            if(abs(a[i][c]) > abs(a[maxi][c]))
                maxi = i;
        if(maxi != r)
        {
            for(int i=r; i<m+1; i++)
                swap(a[r][i],a[maxi][i]);
        }
        if(a[r][c] == 0)
        {
            r--;
            continue;
        }
        for(int i=r+1; i<n; i++)
        {
            if(a[i][c] != 0)
            {
                int x = abs(a[i][c]);
                int y = abs(a[r][c]);
                int LCM = lcm(x,y);
                int tx = LCM / x;
                int ty = LCM / y;
                if(a[i][c] * a[r][c] < 0)
                    ty = -ty;
                for(int j=c; j<m+1; j++)
                    a[i][j] = ((a[i][j] % 2 * tx % 2 - a[r][j] % 2 * ty % 2) % 2 + 2) % 2;
            }
        }
    }
}

int Rewind(int a[][N],int x[],int r,int c)
{
    for(int i=r-1; i>=0; i--)
    {
        int t = a[i][c] % 2;
        for(int j=i+1; j<c; j++)
        {
            if(a[i][j] != 0)
                t -= a[i][j] % 2 * x[j] % 2;
        }
        x[i] = t / a[i][i] % 2;
        x[i] = (x[i] + 2) % 2;
    }
    return 0;
}

int a[N][N];
int x[N];

int main()
{
    int cas = 1;
    int n,m,T;
    scanf("%d",&T);
    while(T--)
    {
        n = m = 30;
        memset(a,0,sizeof(a));
        for(int i=0; i<5; i++)
        {
            for(int j=0; j<6; j++)
            {
                if(i >= 1) a[6*i+j][6*(i-1)+j] = 1;
                if(i <= 3) a[6*i+j][6*(i+1)+j] = 1;
                if(j >= 1) a[6*i+j][6*i+j-1] = 1;
                if(j <= 4) a[6*i+j][6*i+j+1] = 1;
                a[6*i+j][6*i+j] = 1;
                scanf("%d",&a[6*i+j][30]);
            }
        }
        int r,c;
        int cnt = 0;
        Gauss(a,n,m,r,c);
        Rewind(a,x,r,c);
        printf("PUZZLE #%d\n",cas++);
        for(int i=0; i<30; i++)
        {
            cnt++;
            if(cnt % 6) printf("%d ",x[i]);
            else printf("%d\n",x[i]);
        }
    }
    return 0;
}


 

题目：http://poj.org/problem?id=1830

 

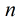
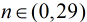
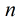
题意：给定个开关，其中，然后给定这个开关的初始状态和最终状态，再给定一些关系，表示操作一

     个开关另一些开关的变化情况，求有多少种方法能从初始状态变为最终状态。

 

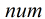
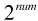
分析：如果只有唯一解，则输出1，如果有多个变元，变元个数为，那么答案等于，否则没有解。

 

代码：

#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
#include <math.h>

using namespace std;
typedef long long LL;
const int N = 35;

int gcd(int a,int b)
{
    return b ? gcd(b,a%b):a;
}

int lcm(int a,int b)
{
    return a / gcd(a,b) * b;
}

void Gauss(int a[][N],int n,int m,int &r,int &c)
{
    r = c = 0;
    for(; r<n && c<m; r++,c++)
    {
        int maxi = r;
        for(int i=r+1; i<n; i++)
            if(abs(a[i][c]) > abs(a[maxi][c]))
                maxi = i;
        if(maxi != r)
        {
            for(int i=r; i<m+1; i++)
                swap(a[r][i],a[maxi][i]);
        }
        if(a[r][c] == 0)
        {
            r--;
            continue;
        }
        for(int i=r+1; i<n; i++)
        {
            if(a[i][c] != 0)
            {
                int x = abs(a[i][c]);
                int y = abs(a[r][c]);
                int LCM = lcm(x,y);
                int tx = LCM / x;
                int ty = LCM / y;
                if(a[i][c] * a[r][c] < 0)
                    ty = -ty;
                for(int j=c; j<m+1; j++)
                    a[i][j] = ((a[i][j] % 2 * tx % 2 - a[r][j] % 2 * ty % 2) % 2 + 2) % 2;
            }
        }
    }
}

LL Rewind(int a[][N],int n,int m,int r,int c)
{
    for(int i=r; i<n; i++)
        if(a[i][c] != 0)
            return -1;
    if(m == r) return 1;
    if(m > r)  return (LL)1<<(m-r);
    if(m < r)  return -1;
}

int a[N][N];
int t1[N],t2[N];

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int num,n,m;
        scanf("%d",&num);
        n = m = num;
        memset(a,0,sizeof(a));
        for(int i=0; i<num; i++)
            scanf("%d",&t1[i]);
        for(int i=0; i<num; i++)
        {
            scanf("%d",&t2[i]);
            if(t2[i] != t1[i])
                a[i][num] = 1;
            a[i][i] = 1;
        }
        while(1)
        {
            int x,y;
            scanf("%d%d",&x,&y);
            if(x == 0 && y == 0) break;
            a[y-1][x-1] = 1;
        }
        int r,c;
        Gauss(a,n,m,r,c);
        LL ans = Rewind(a,n,m,r,c);
        if(ans == -1) puts("Oh,it's impossible~!!");
        else printf("%I64d\n",ans);
    }
    return 0;
}

 

题目：http://acm.hdu.edu.cn/showproblem.php?pid=3359

 

题意：有一个图像模糊处理的算法，图像设置为一定灰度后是一个不太大的矩阵，对这个矩阵通过一个算法处理后得

     到另一个矩阵，那么图像就会变得模糊，这个算法就是求某个元素周围距离在内的平均值。现在给定模糊图

     像的矩阵，把它还原为清晰图像对应的矩阵。具体变换如下图所示

 

                

 

 

分析：这个题比较有意思，涉及到图像处理的算法，当然这个我们可以设每个矩阵里的元素对应一个未知数，那么一

     共有个未知数，而某个元素在距离为以内的所有元素都与它有关系，那么可以得到个方程形成的

     方程组。注意这里的数字为实数，所以不必像整数求最大公约数那样消元，直接做就行了。

 

代码：

#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
#include <math.h>

using namespace std;
const int N = 105;

void Gauss(double a[][N],int n,int m,int &r,int &c)
{
    r = c = 0;
    for(; r<n && c<m; r++,c++)
    {
        int maxi = r;
        for(int i=r+1; i<n; i++)
            if(fabs(a[i][c]) > fabs(a[maxi][c]))
                maxi = i;
        if(maxi != r)
        {
            for(int i=r; i<m+1; i++)
                swap(a[r][i],a[maxi][i]);
        }
        for(int i=r+1; i<n; i++)
        {
            if(a[i][c])
            {
                double t = -a[i][r] / a[r][r];
                for(int j=r; j<m+1; j++)
                    a[i][j] += t * a[r][j];
            }
        }
    }
}

void Rewind(double a[][N],double x[],int n,int m,int r,int c)
{
    for(int i=r-1; i>=0; i--)
    {
        double t = a[i][c];
        for(int j=i+1; j<c; j++)
            t -= a[i][j] * x[j];
        x[i] = t / a[i][i];
    }
}

int dist(int x1,int y1,int x2,int y2)
{
    return abs(x1 - x2) + abs(y1 - y2);
}

double a[N][N];
double t[N][N];
double x[N];

int main()
{
    int n,m;
    int w,h,d;
    bool flag = 1;
    while(scanf("%d%d%d",&w,&h,&d)!=EOF)
    {
        if(w == 0 && h == 0 && d == 0) break;
        if(flag) flag = 0;
        else puts("");
        for(int i=0; i<h; i++)
        {
            for(int j=0; j<w; j++)
                scanf("%lf",&t[i][j]);
        }
        n = m = w * h;
        memset(a,0,sizeof(a));
        for(int i=0; i<h; i++)
        {
            for(int j=0; j<w; j++)
            {
                int cnt = 0;
                for(int k=0; k<h; k++)
                {
                    for(int r=0; r<w; r++)
                    {
                        if(dist(i,j,k,r) <= d)
                        {
                            a[i*w+j][k*w+r] = 1;
                            cnt++;
                        }
                    }
                }
                a[i*w+j][m] = t[i][j] * cnt;
            }
        }
        int r,c;
        Gauss(a,n,m,r,c);
        Rewind(a,x,n,m,r,c);
        for(int i=0; i<h; i++)
        {
            for(int j=0; j<w; j++)
                printf("%8.2f",x[i*w+j]);
            puts("");
        }
    }
    return 0;
}

 

 

 

ACdreamers
关注
专栏目录
hdu 4592（高斯消元好题）
北门的智慧
09-11 1276
题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=4592； 题目分析：  本题其实就是一个普通的高斯消元题，但是本题数据范围巨大，所以不能用普通的高斯消元来写，只能采用求逆打表法，进行求解。只有满秩矩阵才能有逆元，通过消元可以看出，只有4,5时时多解的，所以其他就打表好了，但不能打0,1矩阵，还是会超时，最后打出的是十进制数就好办了。 代码如下：
高斯消元练习题集
Miserable_ccf的博客
11-01 1878
1.POJ-1222 EXTENDED LIGHTS OUT 题意 开关问题，给一个矩阵，每次翻转，上下左右都会一起翻转，问你翻转哪些位置，可以把灯全部关上。 思路 异或运算下的高斯消元 典型的开关问题，和 POJ 1830 开关问题 是一样的属于 XOR 类型的消元。 /*************************** *author:ccf *source:poj-1222- EXTE...
高斯消元法习题课.mp4
07-28
讲述洛谷上5道高斯消元法习题。包括解线性方程组，初等行变换和初等矩阵，矩阵求逆，解决开灯问题，矩阵树定理的应用等等。
hdu 3364 Lanterns 高斯消元，模板题
冷月之殇
09-17 2600
#include #include #include #include #include #include #include #include using namespace std; const int maxn=55; struct matrix{ int f[maxn][maxn]; }e,g; int find(matrix a,int m,int n)//高斯消元
hihoCoder #1195 : 高斯消元·一
weixin_34138139的博客
08-16 89
时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 小Ho：喂不得了啦，那边便利店的薯片半价了! 小Hi：啥?! 小Ho：那边的便利店在打折促销啊。 小Hi：走走走，赶紧去看看=v= 于是小Hi和小Ho来到了便利店。 老板为了促销，推出了组合包的形式，将不同数量的各类商品打包成一个组合，顾客可以选择组合进行购买。比如2袋薯片，1听可乐的组...
【高斯消元】[NOIP2004]虫食算 —— 正解
weixin_30614109的博客
01-30 239
题目描述：所谓虫食算，就是原先的算式中有一部分被虫子啃掉了，需要我们根据剩下的数字来判定被啃掉的字母。来看一个简单的例子： +43a9865a045008468a663344445506978 其中a号代表被虫子啃掉的数字。 根据算式，我们很容易判断：第一行的两个数字分别是5和3，第二行的数字是5。 现在，我们对问题做两个限制： 首先，我们只考虑加法的...
NOIP ACM 高斯消元练习+数据题解
04-01
高斯-约旦消元法是在高斯消元的基础上，通过更多的行初等变换，将系数矩阵直接化为单位阵，从而直接得到解。这种方法更直观，但计算量稍大。 五、应用实例与题解 在NOIP和ACM竞赛中，数据题经常涉及线性方程组的...
数值计算期末复习：牛顿迭代法、高斯消元与插值问题详解
本资源是一份数值计算期末复习的练习题与答案集合，主要涵盖了计算题、填空题...这份期末复习练习题涵盖了数值计算中的基础理论和实际操作技巧，有助于学生巩固和深化对数值方法、线性代数和函数逼近等核心概念的理解。
最新高斯消元法和列主销元法（Python实现）(1)
最新发布
2401_84562659的博客
05-03 905
A[Num - 1], A[i] = A[i], A[Num - 1] # 做行变换。
高斯消元法
热门推荐
蜗牛
04-23 3万+
矩阵，逆矩阵，秩，矩阵方程，参考代码。
poj 1830 高斯消元模版题
T_T
02-25 706
开关问题 Time Limit: 1000MS Memory Limit: 30000K Total Submissions: 6067 Accepted: 2309 Description有N个相同的开关，每个开关都与某些开关有着联系，每当你打开或者关闭某个开关的时候，其他的与此开关相关联的开关也会相应地发生变化，即这些相联系的开关的状态如果原来为开就变为关，如果为关就变为
高斯消元专题训练
HeartWine的博客
11-04 508
文章目录POJ 1222 EXTENDED LIGHTS OUT POJ 1222 EXTENDED LIGHTS OUT 题意： 给定一个555行666列的010101矩阵，每一个小格子代表一个开关，000表示开关关闭，111表示开关闭合，当按下一个开关后，其也会影响该开关上下左右的开关的状态。现在给定一个这样的01矩阵，输出一种方案，使得所有开关都变成闭合状态。 思路：555行666列，相当于一共是303030个未知数，可以根据题意列出303030个方程，然后高斯消元，因为都是010101，所以是解异或
高斯消元入门
juruo_hejiarui的博客
02-24 219
问题 现在有一个 nnn 元一次方程组，类似下面这个样子： {a1,1x1+a1,2x2+...+a1,nxn=b1a2,1x1+a2,2x2+...+a2,nxn=b2...an,1x1+an,2x2+...+an,nxn=bn \begin{cases} a_{1,1}x_1+a_{1,2}x_2+...+a_{1,n}x_n = b_1\\ a_{2,1}x_1+a_{2,2}x_2+...+a_{2,n}x_n = b_2\\ ...\\
【例题】【高斯消元(异或)】
ANG
12-19 2010
1、 NKOJ1985 中央暖气 时间限制 : 10000 MS 空间限制 : 65536 KB问题描述 冬天来了，但URAL大学的暖气系统还没启动。这个暖气系统包括许多阀门，只有所有阀门都打开了才能供应暖气。大学里有一些技术员，他们每人负责一个或多个阀门，有可能存在一个阀门由多个人负责的情况。当一个技术员接到启动暖气系统的指示后他就会把所有自己负责的阀门都转动一次。这意味着如果一个阀门
高斯消元法模板题
give it a try
11-12 281
链接 AC代码 #include <bits/stdc++.h> inline long long read(){char c = getchar();long long x = 0,s = 1; while(c < '0' || c > '9') {if(c == '-') s = -1;c = getchar();} while(c >= '0' && c <= '9') {x = x*10 + c -'0';c = getchar();} retur
闲聊高斯消元入门
Hee的博客~
08-21 793
前言：前一段时间看了看高斯消元，一直想把学习过程写下来，但有点懒=-=现在补上 一、关于高斯消元的题目常见的有： 1 . 求唯一整数解 2 . 求唯一浮点数解 3 . 求解得个数，等同于求自由元个数，矩阵的秩。 然后其中一般都会让你判断无解的情况 二、高斯消元的步骤 第一步：将给定矩阵化成阶梯矩阵。 第二步：根据题目的要求 ： 1 . 判断是否无解  2 . 求
POJ2947 Widget Factory（高斯消元模板题）
geng4512的专栏
05-17 597
传送门 大意：有n个变量，m个等式，求在 模7 意义下的解。 其实就是模板题，消完元之后如果有自由元就是有多个解，如果消完元之后有等式两边不等的情况，就是无解，否则有解。 代码：#include <cstdio> #include <cstring> #include <algorithm> #include <assert.h> using namespace std; #define MA
#1195 : 高斯消元·一（模板题）
qwesde
08-25 484
题目链接高斯消元，使用列主元的方法即可。 如果使用浮点数计算的话，要注意精度问题，还有一个题目的讲解有个小问题，我的提问#include<bits/stdc++.h> using namespace std; #define cl(a,b) memset(a,b,sizeof(a)) #define fastIO ios::sync_with_stdio(false);cin.tie(0); #d
HDU 4592 Boring Game(高斯消元好题)
代码改变世界
09-11 1344
传送门 Boring GameTime Limit: 8000/4000 MS (Java/Others)    Memory Limit: 65535/32768 K (Java/Others)Total Submission(s): 827    Accepted Submission(s): 80Problem Description Zero likes to play a boring
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值