o1推理无上限：集成CoT让Transformer解决P/poly类任意问题

作者：御坂美冰
原文：https://zhuanlan.zhihu.com/p/720520675

这篇文章主要探讨了“链式思维”（Chain of Thought, CoT）如何提升Transformer模型在处理复杂推理任务时的表达能力。其主要观点包括：

• • 链式思维：链式思维是指通过生成中间步骤来增强语言模型的推理能力。特别是在数学运算和符号推理任务中，链式思维被证明是有效的。传统的Transformer模型在没有足够的深度时，难以进行串行计算，而链式思维弥补了这一不足。

• • 理论分析：作者从计算复杂度的角度分析了Transformer模型的表达能力。通过构造布尔电路的类比，证明了在没有链式思维的情况下，固定深度的Transformer只能解决并行可计算的问题。但如果加入链式思维，Transformer可以解决需要串行计算的问题。这意味着通过生成足够多的推理步骤，Transformer能够处理复杂度更高的问题。

• • 链式思维的效果：作者通过实验验证了链式思维的有效性。文章选取了几类需要串行计算的问题，如置换群的组合、迭代平方和电路值问题。结果表明，启用链式思维后，即便是浅层的Transformer模型，也能够显著提升在这些任务上的表现。

• • 链式思维的复杂度类定义：定义了新的复杂度类CoT[T(n), d(n), s(n)]，用于描述使用链式思维的Transformer模型所能解决的问题。这一复杂度类明确了在不同的链式思维步数和嵌入维度下，模型的计算能力。

Paper:Chain of Thought Empowers Transformers to Solve Inherently Serial ProblemsAbs:https://arxiv.org/abs/2402.12875

1. 引言（Introduction）

该部分介绍了大型语言模型（LLM）在复杂推理任务（如数学问题求解和代码生成）方面表现出的卓越能力。文章指出，链式思维（CoT，Chain of Thought）通过生成中间推理步骤来增强这些模型的推理能力。虽然CoT的有效性在实践中已被证明，但其背后的机制尚未完全理解。本文通过理论和实验，分析了CoT如何赋予Transformer模型串行计算能力，这种能力是标准Transformer所不具备的。作者提出，CoT在增强模型的计算能力方面具有关键作用，特别是对于那些需要串行计算的问题。

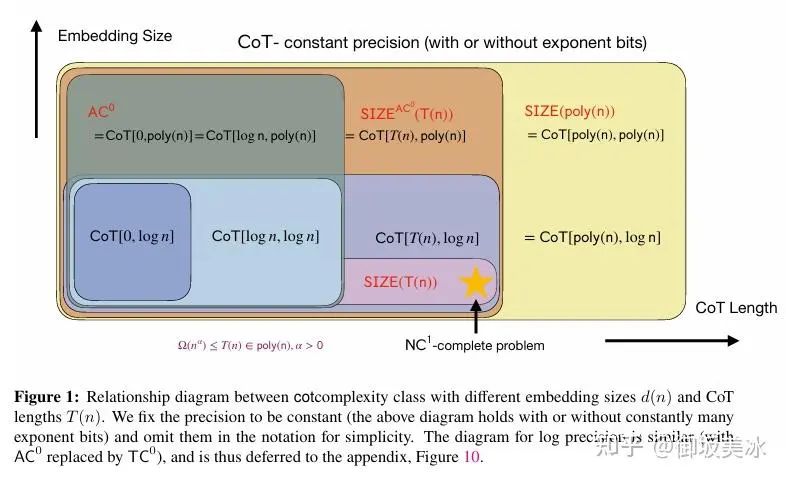
CoT复杂度类的关系图

这个图比较重要，详细介绍一下

• •  ：  是计算复杂度类，表示可以用常数深度的布尔电路解决的问题，这些电路的规模为多项式。它允许无穷多输入的AND和OR门，但不允许门限（多数表决）操作。AC^0类问题是非常简单的并行问题，比如判断所有输入是否全为1。

• • CoT[0, poly(n)]：表示没有链式思维（即CoT步数为0）且嵌入维度是多项式规模（poly(n)）的Transformer只能解决非常简单的并行计算任务，计算能力等同于 AC^0 。

• • CoT[logn, poly(n)]：表示链式思维长度为log(n)且嵌入维度是多项式规模的Transformer。虽然有一些链式思维步数，但由于嵌入维度较大，模型仍然只能处理 AC^0 类的简单并行问题。

：表示一个问题可以用规模为T(n)的 AC^0 电路解决。这种电路可以有效地处理简单的并行计算任务。

• • CoT[T(n), poly(n)]：表示链式思维长度为T(n)，嵌入维度为多项式规模的Transformer模型。链式思维的步数为T(n)，意味着模型可以通过逐步生成推理步骤来处理串行任务。但由于嵌入维度较大，它仍然在AC^0的范围内，适合解决并行问题。

• • SIZE(poly(n))：表示问题可以通过多项式规模的布尔电路来解决，且电路的深度没有限制。这意味着这些电路可以执行多步串行计算，因此可以解决P/poly类问题。P/poly类允许针对不同输入大小生成不同的电路，这使得它比AC^0和TC^0更强大。

• • CoT[poly(n), poly(n)]：表示链式思维长度和嵌入维度均为多项式规模的Transformer。这个模型能够通过逐步生成和处理复杂的推理步骤解决复杂问题，包括P/poly类问题。

• • CoT[poly(n), logn]：表示链式思维长度为多项式，但嵌入维度为log(n)的Transformer。虽然嵌入维度较小，但由于链式思维步数足够多，它可以处理与多项式规模电路相当的问题，因此同样可以解决P/poly类问题。

2. 符号和预备知识

该部分介绍了用于讨论Transformer模型的理论基础和符号。具体内容包括：

• • Transformer模型：描述了Transformer模型的结构，包括嵌入层、位置编码层、注意力机制、多层解码器等。

• • 电路复杂度（Circuit Complexity）：为了分析Transformer的计算能力，文章借鉴了电路复杂度理论。定义了布尔电路、并行计算类（如AC0、TC0）等复杂度类，这些类用于分析模型的计算能力。

3. 具有链式思维的Transformer表达能力（Expressiveness for Transformers with (CoT)）

文章的核心，主要从理论上探讨了具有链式思维的Transformer模型的表达能力。分为以下几个子部分：

3.1. 有限精度模型（Finite Precision Modeling）

讨论了在有限精度（即有限位数的浮点运算）条件下Transformer模型的计算模型。现实中的Transformer训练和推理通常使用16位或32位浮点数，因此该部分详细定义了浮点数的表示方式、舍入规则，以及如何将这些有限精度运算引入Transformer的架构中。

3.2. 带链式思维的Transformer的复杂度类（CoT: Complexity Class for Constant-depth Transformers with CoT）

引入了复杂度类CoT[T(n), d(n), s(n), e(n)]，用于描述具有T(n)步链式思维、嵌入维度为d(n)、精度为s(n)、指数为e(n)的Transformer所能解决的问题。定义了该类的模型，并讨论了这些模型在常深度条件下的计算能力。

3.3. Transformer表达能力的上界（Tighter Upper Bounds on Transformer Expressiveness）

文章首先展示了没有链式思维的情况下，具有常精度和常深度的Transformer只能表达AC0类的问题，即无法进行复杂的串行计算。然后通过复杂度理论证明了，当引入T步的链式思维后，模型可以表达更复杂的计算问题，甚至可以处理由布尔电路解决的问题。

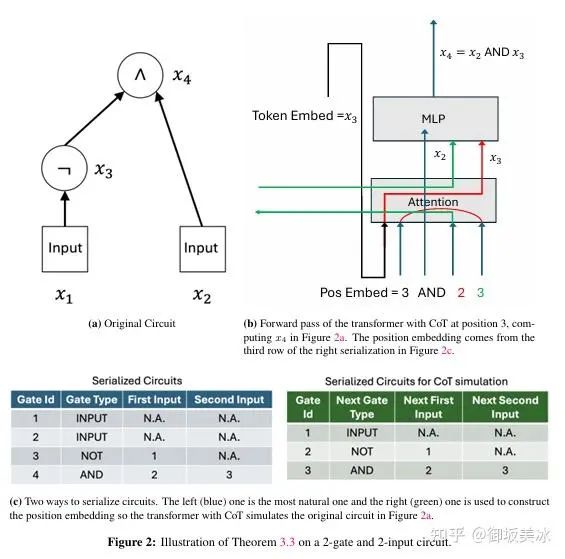
使用CoT模拟布尔电路的Transformer工作机制

• • 图2a：展示了一个布尔电路的示例，其中包含AND、NOT门的组合。

• • 图2b：展示了在CoT的帮助下，Transformer模型如何在特定位置进行串行计算，逐步模拟布尔电路门操作。

• • 图2c ：展示了两种序列化电路的方法，左侧的蓝色序列化是自然的方式，右侧的绿色序列化用于Transformer的位置嵌入，以便在CoT下模拟原始布尔电路。

• • 通过该图，解释了链式思维如何使Transformer能够模拟布尔电路，并通过逐步生成中间步骤来实现复杂的逻辑运算。图2c中的两种序列化方法展示了如何通过位置编码来辅助模型实现这一点。

Theorem 3.1: 固定深度Transformer的表达能力上界

定理内容：对于具有常数位精度的固定深度Transformer，它的表达能力仅限于AC0复杂度类，即无法处理需要计数操作的问题，甚至无法计算二进制字符串的奇偶性。

通俗解释：定理表明，当Transformer的深度固定，且其使用的位数有限时，它只能解决非常简单的并行计算任务。AC0类问题包括像“所有输入位是否全为1”的简单问题，不能处理像奇偶性检查这种涉及计数的任务。
案例：假设你有一个系统，它只能查看非常短的指令序列，不能记住之前发生的事情，也不能累积结果。比如，你让它判断一组灯是否全部亮着（这是一个AC0问题，可以并行判断每个灯），但如果你让它数有多少灯亮着（这是需要串行计数的任务，它就做不到）。

Theorem 3.2: 带有限精度的固定深度Transformer的TC0表达能力

• • 定理内容：当Transformer的深度固定，且精度为对数级别（即更多位数用于计算）时，它的表达能力可以扩展到TC0复杂度类。TC0允许多数表决操作，比如计算“超过一半的输入为1”。

• • 通俗解释：这个定理展示了如果我们允许Transformer有更多位数的精度，虽然它仍然是固定深度的，它可以处理更复杂的任务。TC0类问题包括像“多数决策”这样的任务，即判断输入中1的数量是否超过一半。

• • 案例：想象一个系统，它可以数出多少灯亮着，并做出决策，比如“是否超过一半的灯亮着”。这个任务比简单地检查所有灯是否都亮（AC0）更复杂，但Transformer通过增加位数可以解决这个问题。

3.4. 链式思维使Transformer更具表达力（CoT Makes Transformers More Expressive）

通过理论证明，链式思维显著提升了Transformer的计算能力。例如，具有多项式数量的链式思维步骤的Transformer可以解决多项式时间可解的问题（P/poly）。这一结果表明，链式思维将常深度的Transformer模型的计算能力从AC0提升到了更高的复杂度类。

Theorem 3.3: 链式思维显著提升Transformer的表达能力

• • 定理内容：带有T步链式思维的固定深度Transformer（使用对数级别的嵌入维度和常精度），可以表达所有由大小为T的电路所能计算的函数。特别地，带有多项式长度链式思维的Transformer可以解决P/poly问题类中的所有问题。

• • 通俗解释：如果我们允许Transformer生成中间步骤（即链式思维），即使它的深度保持固定，也可以解决更复杂的任务。通过逐步生成中间推理步骤，Transformer可以执行串行计算，这使得它能够处理更复杂的任务。

• • 案例：假设你想让一个系统完成一系列任务，每个任务需要依赖上一个任务的结果。原本这个系统只能并行处理一些简单任务，但现在你允许它逐步生成每个任务的中间结果，并用这些结果作为后续任务的输入（这就是链式思维）。结果，它能够处理复杂的流程，比如分步骤进行某种复杂的运算，类似于计算机执行一连串操作。

Corollary 3.4：所有正则语言都属于 CoT[n,log⁡n,1]

• • 推论内容：所有正则语言（regular languages）都可以通过使用链式思维步数为n、嵌入维度为log(n)、常数精度的Transformer模型来识别。

• • 正则语言：可以由有限自动机（finite automaton）识别的语言，通常用正则表达式表示，适合表示有限的模式匹配问题，如字符串的简单匹配、有限状态的输入序列处理。

• • CoT[n, logn, 1]：意味着模型使用n步的链式思维（逐步生成中间推理步骤），每个输入的嵌入维度是对数级别（logn），表示Transformer每次处理的信息量受限于输入长度的对数，但这足以处理正则语言。

• • 通俗解释：没有链式思维的限制：如果没有链式思维，传统的Transformer模型只能通过并行计算检查局部模式，无法处理状态之间的依赖。引入链式思维：通过链式思维，模型可以逐步处理输入序列，在每一步更新内部状态。相当于模拟了有限状态机的逐步状态转移，每次读取一个字符，决定是否转换到下一个状态。

Theorem 3.6: 置换群的字问题（Wording Problem of S5）可以通过链式思维解决

• • 定理内容：假设TC0和NC1复杂度类不同（这是复杂度理论中的一个广泛接受的假设），那么置换群S5的字问题（即判断一组置换的组合是否为单位置换）可以由带有链式思维的Transformer解决，但无法通过不带链式思维的Transformer解决。

• • 通俗解释：这个定理表明，链式思维可以让Transformer解决非常复杂的数学问题，像置换群中的字问题，这是典型的需要串行计算的问题，无法通过简单的并行方式解决。

• • 案例：假设你有五张卡片，每张卡片都有不同的排列方式。你想知道一连串的操作后，这些卡片是否恢复到了初始顺序。这个问题涉及多步串行操作，原本Transformer可能无法解决，但通过链式思维，它能够逐步计算每个排列后的结果，最终判断是否恢复原始状态。

Theorem 3.7 和 3.8: 大嵌入尺寸下的Transformer表达能力

• • 定理内容：对于多项式步数的链式思维，具有对数精度（Theorem 3.7）或常精度（Theorem 3.8）的Transformer能够模拟TC0（或AC0）类的所有电路。即使Transformer嵌入尺寸从对数级别扩展到多项式级别，链式思维的引入依然能显著提升模型的表达能力。

• • 通俗解释：如果我们允许模型使用更大的嵌入维度，模型在具有链式思维的条件下能解决更复杂的问题，甚至可以模拟更强的并行电路类。这意味着模型可以使用更丰富的信息来处理并行和串行计算。

• • 案例：可以把这类问题想象成拥有更大内存的计算机，它可以一次处理更多的信息。如果它有足够多的链式思维步骤，它不仅可以处理简单的并行计算，还能解决那些需要多步推理和复杂运算的任务。

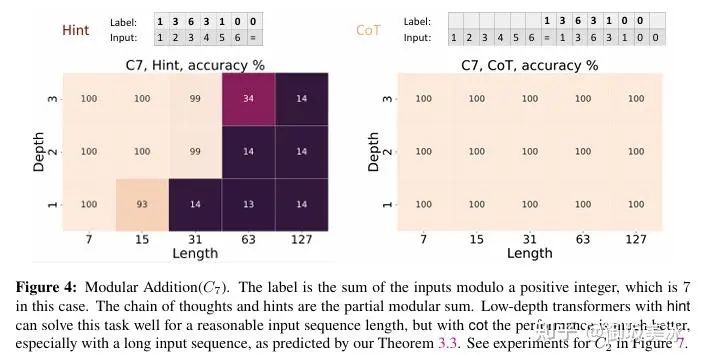
模加运算（C7）的实验结果图

• • 展示了一个模7加法问题的输入、输出和链式思维的中间步骤。输入为一系列数字，输出为这些数字的模7和。链式思维的标签是部分模和的结果。该图用于展示在模加运算任务中，启用链式思维能够有效提高Transformer模型在长序列输入情况下的性能。尤其是在较长的输入序列中，链式思维帮助模型更好地处理累积的模加运算

Theorem 3.9: 具有多项式CoT和多项式嵌入尺寸的Transformer比对数嵌入尺寸的Transformer更强

• • 定理内容：对于多项式步数的链式思维，Transformer如果嵌入尺寸从对数级别增加到多项式级别，其计算能力将显著增强，能够解决更多的复杂问题。

• • 通俗解释：这个定理表明，除了链式思维的步数外，嵌入维度的增加也会使Transformer的计算能力更强。当嵌入维度较大时，模型能够存储和处理更多的信息，从而解决复杂度更高的问题。

• • 案例：想象你有一个计算器，它不仅有很强的处理能力（链式思维），而且还有很大的内存（多项式级别的嵌入尺寸）。这个计算器不仅能一步步处理复杂的运算，还能同时保存大量的中间结果和信息，确保最终结果更加准确和全面。

4. 链式思维在低深度Transformer上的实证性提升（CoT Empirically Improves Expressiveness of Low-Depth Transformers on Inherently Serial Problems）

该部分通过实验验证了链式思维在提高Transformer模型解决复杂问题时的表现。实验任务包括：

• • 模加运算（Modular Addition）：该任务易于并行计算，因此标准的Transformer可以很好地解决该问题。

• • 置换群组合（Permutation Composition）：这是一个复杂的串行计算问题，实验显示只有引入链式思维后，模型才能很好地解决。

• • 迭代平方问题（Iterated Squaring）：一个难以并行计算的问题，使用链式思维的Transformer在这个任务上表现优异。

• • 电路值问题（Circuit Value Problem, CVP）：这是一个P类完全问题，需要串行计算。实验结果证明，启用链式思维后，模型表现显著提高。

通过这些实验，文章验证了理论预测，即链式思维可以增强Transformer在串行计算任务中的能力，特别是对于那些传统上很难并行计算的问题。

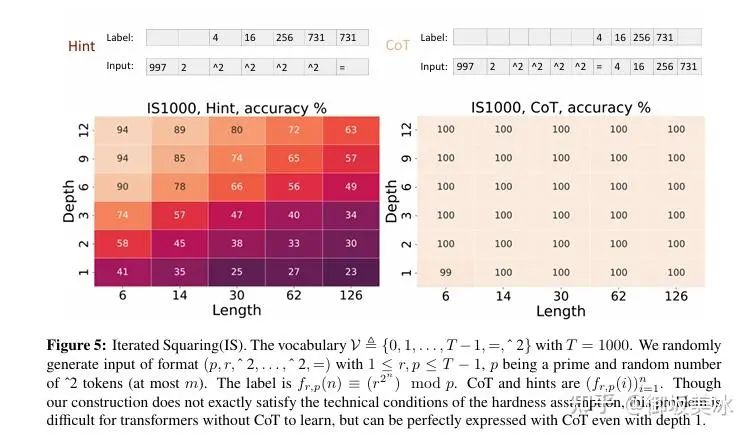
迭代平方问题的实验结果图

展示了迭代平方问题的实验设置和链式思维的中间步骤。输入为一个随机生成的质数和若干次幂运算的组合，输出为相应的模运算结果。链式思维通过提供每次平方的中间结果来帮助模型进行推理。通过该图展示了链式思维在处理迭代平方问题上的有效性。没有链式思维的Transformer难以学会这个问题，但启用链式思维后，模型能够准确地进行推理，甚至在浅层Transformer中也表现良好。

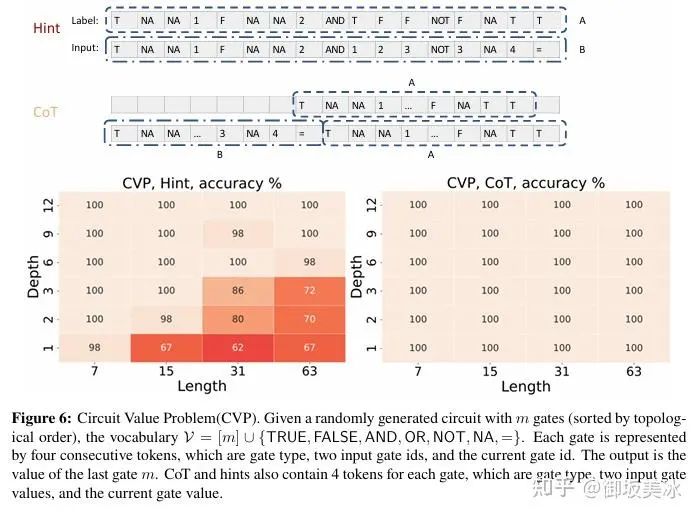
电路值问题的实验结果图

展示了电路值问题的实验设置和链式思维的中间步骤。输入为一个随机生成的布尔电路，包含若干门类型及其输入和输出。链式思维通过提供每个门的中间输出值，帮助模型进行推理。通过该图展示了在电路值问题上，链式思维帮助Transformer模型更好地处理这种P类完全问题。启用链式思维后，模型的推理能力显著提升。

5. 其他补充

1.CoT的集成缩小了Transformer与图灵机之间的差距？

• • Transformer的局限性：经典的Transformer模型是一种“并行”计算模型，其架构擅长处理并行计算任务，但由于深度有限，它无法直接处理那些本质上需要串行计算的复杂任务。并行计算意味着在多个独立任务上可以同时进行操作，但串行计算则要求任务一步接一步地完成。

• • 链式思维的作用 ：CoT通过允许模型生成中间推理步骤，使得Transformer可以逐步完成计算任务。这种机制弥补了Transformer在处理串行问题上的不足，使得它能够处理需要多个步骤依次完成的复杂问题，比如解决置换群的问题，或模拟布尔电路中的逐步运算。通过在每一步生成并利用前一步的中间结果，链式思维让Transformer更像图灵机，因为它可以有效地“记住”每一步的计算结果，并将其用于后续推理。

因此，CoT的集成缩小了Transformer与图灵机之间的差距，因为它赋予了Transformer某种形式的记忆和序列处理能力，这是图灵机具备的关键特性。Transformer不仅能够解决并行任务，还能够通过串行推理解决复杂问题。

2. 怎样的Transformer是图灵完备的？

要实现图灵完备，Transformer必须具备一些关键特性，这些特性确保模型能够模拟图灵机执行的任意计算任务：

无界的存储

• • 图灵机的存储能力是无界的，即它可以使用无限长的磁带来存储信息。对于Transformer，要实现图灵完备，它需要在某种形式上能够处理“无限长度”的输入序列或生成无限长的推理链。

• • 链式思维虽然为模型提供了在固定输入长度内的多步推理能力，但它仍然受限于Transformer的有限深度和输入序列长度。为了实现图灵完备，Transformer需要具备扩展性，能够处理非常长的输入或产生非常长的推理链。

循环与递归能力

• • 图灵机能够执行循环和递归，重复执行某些操作直到满足某种条件。对于Transformer，它需要能够在不受限的情况下重复处理某些输入或中间结果。经典的Transformer架构由于层数有限，无法实现无限循环或递归计算。

• • 为了实现图灵完备，Transformer需要引入某种记忆机制或递归结构，如自循环网络（RNN）或堆栈结构，允许它在有限深度内模拟循环或递归过程。

条件分支

• • 图灵机可以根据条件做出不同的计算路径选择。对于Transformer，它需要具有根据中间推理结果选择不同操作路径的能力。这种条件分支可以通过注意力机制或额外的控制信号实现，允许Transformer根据特定的条件进行不同的计算。

• • 链式思维在一定程度上提供了这类能力，因为它允许模型根据先前的中间推理结果决定下一步操作，但为了完全实现图灵完备，还需要更灵活的分支选择机制。

所以图灵完备的Transformer需要满足以下条件：

• • 无限长的输入和输出序列，这意味着模型需要能够处理和生成任意长的序列，而不受输入长度的限制。

• • 循环结构或递归能力，例如通过引入某种形式的记忆机制（如RNN的自回路）来模拟图灵机的磁带操作。

• • 条件分支能力，模型需要能够根据推理过程中产生的中间结果选择不同的计算路径。

3.计算复杂性类

是一个计算复杂度类，它代表可以在常数深度下使用多项式规模的布尔电路解决的问题。

是一个计算复杂度类，它代表可以在对数深度下用多项式规模的布尔电路解决的问题。

 -complete问题是该类中最难的问题。即，该类中的任何问题都可以被化简为complete问题。

是另一个复杂度类，代表可以使用多项式规模且深度为常数的布尔电路解决的问题

是一个非均匀复杂度类，表示可以用多项式规模的布尔电路解决的问题。它不限制电路的深度，但电路的规模必须是多项式的。

P类问题：通过一个确定性图灵机在多项式时间内解决。这是经典复杂度类之一，代表那些可以有效计算的问题。

NP类问题：可以在多项式时间内验证其解的问题，即给定一个问题的解后，可以在多项式时间内验证解是否正确。NP问题的求解时间可能是指数级，但其解可以在多项式时间内验证。

EXPTIME类问题：可以通过确定性图灵机在指数时间内解决的问题，即其计算时间是输入规模的指数函数。通常，EXPTIME问题比P和NP类问题要难得多。

PSPACE类问题：可以在多项式空间内解决的问题，意味着问题的求解过程中使用的内存是输入规模的多项式级别。它包括所有可以在多项式空间内解决的确定性和非确定性问题。

BPP问题（Bounded-error Probabilistic Polynomial Time，带有错误概率的多项式时间）：可以通过随机算法在多项式时间内解决的问题，并在大多数情况下（概率至少为2/3）能给出正确答案。

LSpace问题：可通过确定性图灵机在对数空间内解决的问题。问题求解过程只需使用输入规模对数级别的内存。

NL类问题：可以通过一个非确定性图灵机在对数空间内解决的问题。

4.计算复杂性类的关系

• • 电路类: AC^0 ⊆ TC^0 ⊆ NC^1

• • 时空类:NC^1 ⊆ L ⊆ NL ⊆ P ⊆ NP ⊆ PSPACE ⊆ EXPTIME

• • 非均匀类:P ⊆ P/poly

• • 概率类:P ⊆ BPP ⊆ P/poly

5.千禧年数学难题的计算复杂度

黎曼猜想（Riemann Hypothesis）

黎曼猜想是关于黎曼ζ函数的非平凡零点分布的猜想。具体地，它提出所有非平凡的ζ函数零点都位于复平面的实部为1/2的直线上。黎曼猜想尚未被完全证明或反驳，属于开放性问题，因此很难直接将其归类为某种确定的计算复杂性类问题。黎曼猜想的复杂性可能涉及高维、非线性问题的深刻数学结构，尽管其验证过程可以通过数值方法进行有限精度的计算（即尝试验证一些零点的位置），但没有已知的多项式时间算法来验证其全部结论，因此它可能属于非常高阶的复杂性问题，如EXPTIME甚至更高的类。

霍奇猜想（Hodge Conjecture）

霍奇猜想涉及代数几何中的拓扑问题，提出在代数簇上，某些同调类可以用代数循环来表示。霍奇猜想是一个深刻的几何和拓扑问题，目前没有已知的直接算法表述。因此，很难将其归类为P类、NP类或更高阶复杂性问题。由于涉及代数几何中的高维几何结构，它可能属于超出P和NP复杂性类的问题。

Poincaré猜想

Poincaré猜想已经在2003年由佩雷尔曼（Grigori Perelman）成功证明。该猜想是拓扑学中的一个重要问题，提出了关于三维闭合流形的特性。在被证明之前，Poincaré猜想是一个非常难解的拓扑问题，属于几何拓扑复杂性类。佩雷尔曼通过黎曼几何和Ricci流等高阶数学工具解决了这个问题，这些方法本质上涉及非常复杂的高维非线性计算和分析。。

其他千禧年难题

• • Yang-Mills存在性与质量缺口（Yang-Mills Existence and Mass Gap）：涉及理论物理中的量子场论问题，复杂性可能与物理模拟和数值计算密切相关。

• • BSD猜想（Birch and Swinnerton-Dyer Conjecture）：涉及数论中椭圆曲线的有理点和L函数，复杂性可能非常高，甚至与NP或更高阶复杂性类相关。

• • 纳维-斯托克斯方程的存在性与光滑性（Navier-Stokes Existence and Smoothness）：涉及流体力学中的偏微分方程，计算复杂性可能与PDE的数值求解和混沌动力学相关。

所以即使o1的方法可以无上限使用（不考虑成本），但也解决不了这些千禧年难题。