【机器学习】拉格朗日乘子法求解最优化问题

目录

引言：

一个约束条件例子：

多个约束条件：

---

引言：

拉格朗日乘子法是解决带有约束条件的优化问题的一种常用方法，也适用于不等式约束条件。它的基本思想就是用过拉格朗日乘子来把含有m个变量和n个约束条件的约束优化问题转换成含有（m+n）个变量的无约束优化问题。

一个约束条件例子：

以一个一元函数为例，假设有一个约束条件g(x)≤0，原优化问题可以描述为：

函数：min f(x)

约束条件：s.t. g(x)≤0

引入拉格朗日乘子λ，整合得到拉格朗日函数L(x,λ)：

L(x,λ) = f(x) + λg(x)

其中，λ为拉格朗日乘子。

为求解原问题，我们要分别对目标函数和约束条件分别求导得到：

∂L/∂x = ∂f/∂x + λ∂g/∂x = 0

∂L/∂λ = g(x) ≤ 0

由于g(x)≤0，故λ≥0。

因此，我们可以得到拉格朗日方程组：

∂f/∂x + λ∂g/∂x = 0

g(x) ≤ 0

λ ≥ 0

λg(x) = 0

最后，我们解出拉格朗日方程组即可得到原问题的最优解。

需要注意的是，由于有不等式约束条件，故约束条件不一定在最优解处取到等号，因此需要对约束条件的取等和不取等情况进行分类讨论，去掉不满足条件的解，最终得到该问题的最优解。

多个约束条件：

我们要求解的函数为：

 求解多个约束条件下的最小值，形式如下：

整合函数得到：（为拉格朗日乘子）

修改目标函数： 

修改约束条件：

 整合后结果为：

约束条件为：

然后利用对偶性质求解： 

 可得：

再根据已知条件代入计算： 

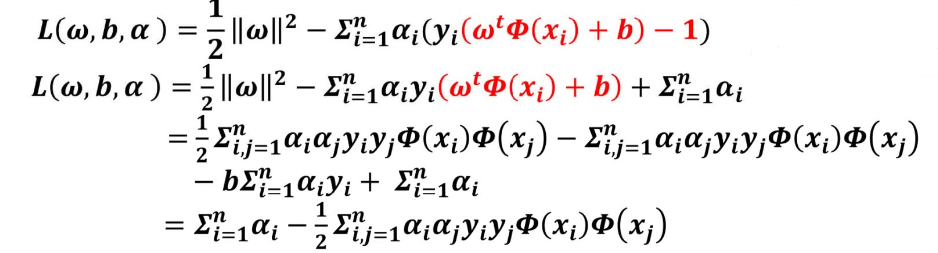
 最后根据约束条件：

最后可求得约束条件下的最小值。