PCA降维的推导（超详细）

最新推荐文章于 2023-12-31 16:20:50 发布
最新推荐文章于 2023-12-31 16:20:50 发布
阅读量1.2k 收藏 6
点赞数 1
文章标签： 人工智能 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/AI_dataloads/article/details/133689402
版权
本文介绍了PCA（主成分分析）作为一种常见的数据降维方法，通过找出数据的主要特征，减少冗余，优化数据表示。文章详细阐述了PCA的数学推导过程，包括中心化、协方差矩阵、特征值和最大特征值的寻找，以及降维的实际步骤。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

目录

前言

什么是PCV降维

应用场景

PCA的数学推导

PCA降维的过程

PCA的流程

前言

什么是PCV降维

PCA（Principal Component Analysis）是一种常用的降维技术，即将高维数据转换为低维数据的方法。通俗地说，PCA降维就是通过找到数据中的主要特征，并将其用较少的特征来表示，从而减少数据的维度。

下图为例，所有的数据是分布在三维空间中，PCA将三维数据映射到二维平面u，二维平面由向量<u1,u2>表示，u1与u2垂直

应用场景

假设你有一个数据集，它有很多特征（维度），比如说100个。但是你发现这些特征之间可能存在冗余或者相关性，有些特征对数据的贡献可能不是很大。在这种情况下，你可以使用PCA来降低数据的维度。

PCA的数学推导

假设对n个样本x_{i}进行PCA处理，先对数据进行中心化，即将数据的均值变为0（为了后面计算的方便，不用减去mean）

则数据集的协方差矩阵为：

由于上面已经将数据中心化\mu _{i},\mu _{j}均为0，所以这里的协方差可以简化为下面的式子

PCA的主要目的是找到一个线性变换，让数据投影的方差最大化

内基的补充

假设找到线性变化\mu _{1}单位向量）,对x _{i}做线性变化的投影,可知:

然后计算投影后的均值和方差

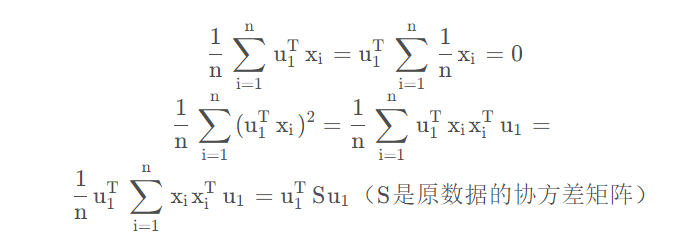
我们要投影后的方差取最大，可以得到优化函数，如下

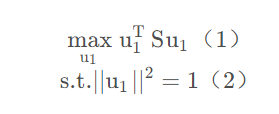
这里的（1）是我们的目标函数，（2）是约束条件，然后构建拉格朗日函数得

要求得（1）式的max，即要λ \lambdaλ最大，而λ \lambdaλ是矩阵S的特征值，问题就转换为求S的最大特征值，求解的方法有SVD矩阵分解和特征值分解。

PCA降维的过程

  • x投影后的方差，就是x协方差矩阵的特征值，想要方差最大，就是要找协方差矩阵最大的特征值，最佳投影方向就是最大特征值对应的特征向量
  • 协方差的特征值有特征向量有\lambda _{1},\lambda _{2},.....\lambda _{n},特征向量有\mu _{1},\mu _{2},....\mu _{n}
  • 将所有特征值从大到小排列，将相应的特征向量随之排列，选择特征向量的前k行组成的矩阵(\mu _{1},\mu _{2},....,\mu _{k})乘以原始数据矩阵X，就得到我们需要的降维后的数据矩阵Y

PCA的流程

假设n个d维样本x_{i}进行PCA处理

  • 将原始数据按列组成d行n列矩阵X
  • 将X的每一行去中心化，即减去这一行的均值
  • 求出X的协方差矩阵
  • 求出协方差矩阵的特征值和对应的特征向量
  • 将特征向量根据对应的特征值大小从上到下按行排列，取前m行组成矩阵P
  • Y=PX即为降维到m维的数据
AI_dataloads
关注
PCA降维全过程
Deepin_L的博客
10-31 1954
PCA的目的 将原有的d维数据集，转换成k维的数据（k<d） 新生成的k维数据尽可能的包含原来d维数据的信息 PCA的数学推导 假设对n个样本xix_ixi​进行PCA处理，先对数据进行中心化，即将数据的均值变为0（为了后面计算的方便，不用减去mean） 1N∑i=1Nxi=0 \frac{1}{N}\sum_{i=1}^{N}x_i=0 N1​i=1∑N​xi​=0 则数据集的协方差矩阵为 Cov(xi,xj)=1n∑i=1n(xi−μi)(xj−μj) Cov(x_i,x_j)=\frac{1
知识：PCA降维
weixin_44340277的博客
02-18 2872
参考了两篇关于PCA的帖子： CodingLabs - PCA的数学原理 【机器学习】降维——PCA（非常详细） - 知乎 里面讲的比较详细，我只做个小简化 PCA（Principal Component Analysis）：用于高维数据的降维，可用于提取数据的主要特征分量 这里需要一些数学的基础知识： 1. 内积和投影 设 A=(x1,y1)，B=(x2,y2)，那么A·B = x1*x2 + y1*y2 =|A|*|B|*cos(α)（α...
PCA数学推导过程
03-19
PCA降维过程的数学简单推导
pca降维详细过程
weixin_34406086的博客
05-18 160
pca降维详细计算过程 转载于:https://www.cnblogs.com/Wanggcong/p/5505799.html
PCA主成分分析（降维）过程推导
以梦为马，不日抵达。
12-22 1万+
主成分分析的作用是降维。当数据量有多个维度时，有些维度对于数据的贡献大，有些维度对数据的贡献小。通过主成分分析，找到重要的维度，能大大减少计算量。 PCA的中心思想： 一个中心：原始特征空间的重构。 两个基本点：最大投影方差，最小重构距离。 --------------------------------------------------------------------------------------------------------------------------------...
PCA数据降维详解
weixin_30745553的博客
02-25 116
转：PCA数据降维详解 转载于:https://www.cnblogs.com/akrusher/articles/6442541.html
PCA降维推导
weixin_33724046的博客
07-28 152
为什么80%的码农都做不了架构师？>>> ...
PCA降维算法讲解和公式推导
08-21
"PCA降维算法讲解和公式推导" PCA（Principal Component Analysis，主成分分析）是一种常用的降维算法，旨在将高维数据转换为低维数据，同时保留原始数据的主要信息。PCA的思想是将原始数据投影到新的坐标系上，...
pca降维的基本思想_三种常用降维方法的思想总结
weixin_42554151的博客
01-17 2026
一.判别分析降维LDA降维和PCA的不同是LDA是有监督的降维，其原理是将特征映射到低维上，原始数据的类别也能清晰的反应在低维的数据上，也就是低维的数据也可以用来判别分类。我们先看看二维的情况，我们希望找到一个向量，使得数据点映射到这个向量上后，两个类间的距离尽可能，两个类内的样本的距离尽可能小。这样就得到了一个目标函数，分子是投影后两个类间均值的差的平方，我们希望这个值尽可能大，分母是投影后的类...
python实现pca降维_PCA降维的原理、方法、以及python实现。
weixin_39520988的博客
12-03 1667
参考：菜菜的sklearn教学之降维算法.pdf!!PCA(主成分分析法)1. PCA(最大化方差定义或者最小化投影误差定义)是一种无监督算法，也就是我们不需要标签也能对数据做降维，这就使得其应用范围更加广泛了。那么PCA的核心思想是什么呢？例如D维变量构成的数据集，PCA的目标是将数据投影到维度为K的子空间中，要求KPCA其实就是方差与协方差的运用。降维的优化目标：将一组 N 维向量降为 K 维...
PCA算法推导过程及案例分析
10-17
即主成分分析技术，又称主分量分析。主成分分析也称主分量分析，旨在利用降维的思想，把多指标转化为少数几个综合指标。
主成分分析（PCA）降维
m0_62501000的博客
12-31 7772
在机器学习和数据分析领域，主成分分析（PCA）是一种常用的降维技术，旨在减少数据维度并保留主要信息。通过将高维数据映射到低维空间，PCA使得数据更易于可视化、理解和处理。本文将深入探讨PCA的原理、应用和实现。通过去除冗余信息，减少数据的维度，提高计算效率和模型训练速度。选择主成分相当于选择了原始特征中最具代表性的信息，有助于提取关键特征。PCA可以帮助去除数据中的噪音，提高模型的鲁棒性。PCA基于线性变换，可能无法很好地处理非线性关系。对异常值敏感，可能受到极端值的影响。
PCA———降维方法详解
watermel__的博客
03-19 185
一篇非常好的PCA讲解文章 转载于【机器学习】降维——PCA（非常详细） - 阿泽的文章 - 知乎 https://zhuanlan.zhihu.com/p/77151308
《推荐系统学习（二）》PCA降维方法的数学推导
qq_30841655的博客
06-25 339
前言 PCA降维方法将一组数据看成是一个随机变量生成的，通过将这个随机变量投影到待找的基向量上，这个投影后得到的一维随机向量方差最大。这个待找的基向量方向上，能够将投影后的数据最大程度区分开来。 推导 输入：数据集 T={x1,x2,...,xN}T=\{x_1, x_2, ..., x_N\}T={x1​,x2​,...,xN​}，xi∈Rnx_i\in\mathbb{R}^nxi​∈Rn；目标维数 kkk 输出：降维后的数据集 T={x1,x2,...,xN}T=\{x_1, x_2, ..., x_
图解机器学习算法(14) | PCA降维算法详解（机器学习通关指南·完结）
ShowMeAI研究中心
03-11 1万+
PCA（主成分分析）可以在对数据完成降维「压缩」的同时，尽量减少信息损失。本文讲解PCA算法的原理、步骤与Python代码实践，并讲解PCA的必要数学基础知识——基变换、方差、协方差等。
PCA推导
qq_36018024的博客
03-08 157
PCA推导
PCA降维的原理及步骤
热门推荐
每天进步一点点
04-10 5万+
*****降维的作用***** ①数据在低维下更容易处理、更容易使用； ②相关特征，特别是重要特征更能在数据中明确的显示出来；如果只有两维或者三维的话，更便于可视化展示； ③去除数据噪声 ④降低算法开销 *****降维通俗点的解释***** 一些高维度的数据，比如淘宝交易数据，为便于解释降维作用，我们在这假设有下单数，付款数，商品类别，售价四个维度，数据量上百万条，对于下单
PCA降维(公式推导)
TH_NUM的博客
05-09 1269
PCA PCA线性投影降维的方法。当维度p高，样本少。 p>> N , S=1NXXT S= \frac{1}{N}XX^T S=N1​XXT 因为 xn是Rp×1x_n 是 R^{p \times 1}xn​是Rp×1 所以Rank(xnxnT)≤1Rank(x_nx_n^T) \leq 1Rank(xn​xnT​)≤1 所以 Rank(S)≤NRank(S) \leq NRank(S)≤N 这种情况下，矩阵运算的复杂度O(p3)O(p^3)O(p3)，浪费了很多的时间，得到了很多是0的矩阵。
pca降维算法
最新发布
03-28
<think>好的，用户想了解主成分分析（PCA）的工作原理和实现方法。首先，我需要回顾一下PCA的基本概念，确保自己理解正确。PCA是一种通过线性变换将高维数据投影到低维空间的技术，保留数据的主要特征，常用于降维和去噪。 接下来，我应该分步骤解释PCA的工作原理。第一步通常是数据标准化，确保每个特征的均值为0，方差为1，这样不同量纲的特征不会影响结果。然后计算协方差矩阵，协方差矩阵能反映特征间的相关性，这对找到主成分很重要。 接下来是计算协方差矩阵的特征值和特征向量。这一步是关键，因为特征向量代表了数据的主成分方向，而对应的特征值则表示了各个主成分的重要性，即方差大小。按特征值从大到小排序，选择前k个特征向量作为新的坐标轴，这样就能将数据投影到这些主成分上，实现降维。 用户可能需要具体的实现步骤，比如如何用代码实现。Python中使用NumPy和sklearn是比较常见的方法。我需要写出示例代码，并解释每一步的作用，比如标准化数据、计算协方差矩阵、特征分解等。同时，提醒用户在实际应用中使用sklearn的PCA类会更方便，但自己实现有助于理解原理。 还要注意用户提供的引用内容，特别是引用[1]到[4]，需要适当引用到回答中。例如，引用[1]提到PCA通过线性组合提取信息，引用[2]和[4]提到了代码实现，可以结合起来说明。 用户可能对数学推导有疑问，比如为什么选择协方差矩阵，或者为什么要用特征值分解。这时候需要解释协方差矩阵反映了变量之间的关系，而特征向量则指向方差最大的方向，也就是数据变化最显著的方向，这样保留的主成分能最大程度保留原始数据的方差，减少信息损失。 另外，可能需要解释方差贡献率，即选择多少个主成分合适，通常通过累计贡献率超过某个阈值（如95%）来决定k的值。这部分在数学推导中可以提到特征值的累加比例。 在实现方法中，手动实现和库函数调用的对比也很重要。手动实现有助于理解，但实际应用中使用库函数更高效，特别是处理大数据时。 最后，生成相关问题需要考虑用户可能进一步想知道的内容，比如PCA的优缺点、优化方法、与其他降维技术的对比等。根据引用[3]，提到PCA与最大可分性的关系，可以引导用户深入理解其数学基础。 需要检查是否遵循了系统级指令，比如数学公式使用$...$和$$...$$，LaTeX语法正确，引用标识自然添加。例如，在解释协方差矩阵时用$$...$$单独成段，特征值分解的公式也用正确格式。 总结下来，回答的结构应该是：原理分步骤讲解，数学推导，手动实现代码，库函数使用示例，最后相关问题。确保每个部分都清晰，并引用适当的参考文献。</think>### 主成分分析(PCA)降维算法详解 主成分分析（PCA）是一种通过正交变换将高维数据投影到低维空间的无监督降维方法，其核心目标是保留数据中的最大方差信息[^1]。以下从原理和实现两个层面进行说明： --- #### 一、工作原理（数学推导） 1. **数据标准化** 对原始数据矩阵$X$（$n$个样本，$m$维特征）进行标准化，使每个特征均值为0，方差为1： $$ z_{ij} = \frac{x_{ij} - \mu_j}{\sigma_j}, \quad \mu_j = \frac{1}{n}\sum_{i=1}^n x_{ij}, \quad \sigma_j = \sqrt{\frac{1}{n}\sum_{i=1}^n (x_{ij} - \mu_j)^2} $$ 2. **计算协方差矩阵** 协方差矩阵反映不同特征间的相关性： $$ C = \frac{1}{n} Z^T Z $$ 其中$Z$为标准化后的数据矩阵。 3. **特征值分解** 对协方差矩阵$C$进行特征分解，得到特征值$\lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_m$和对应的特征向量$v_1, v_2, \dots, v_m$。每个特征向量代表一个主成分方向[^3]。 4. **选择主成分** 根据方差贡献率（$\frac{\lambda_i}{\sum \lambda_j}$）选择前$k$个主成分，构造投影矩阵$W = [v_1, v_2, \dots, v_k]$。 5. **数据投影** 将原始数据投影到低维空间： $$ Y = Z \cdot W $$ 其中$Y$为降维后的$n \times k$维矩阵。 --- #### 二、实现方法（Python示例） **手动实现步骤** ```python import numpy as np # 1. 数据标准化 def standardize(X): mean = np.mean(X, axis=0) std = np.std(X, axis=0) Z = (X - mean) / std return Z # 2. 计算协方差矩阵并特征分解 def pca(Z, k): cov_matrix = np.cov(Z, rowvar=False) eigenvalues, eigenvectors = np.linalg.eigh(cov_matrix) sorted_indices = np.argsort(eigenvalues)[::-1] top_k_indices = sorted_indices[:k] W = eigenvectors[:, top_k_indices] return Z @ W # 示例调用 X = np.random.rand(100, 5) # 100样本，5维特征 Z = standardize(X) Y = pca(Z, 2) # 降维至2维 ``` **使用scikit-learn库** ```python from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler scaler = StandardScaler() Z = scaler.fit_transform(X) pca = PCA(n_components=2) Y = pca.fit_transform(Z) ``` --- #### 三、关键点说明 1. **最大可分性**：PCA通过最大化投影方差保留数据可分性，数学上等价于协方差矩阵的特征值分解[^3]。 2. **正交性约束**：主成分之间相互正交，消除冗余信息。 3. **应用场景**：图像压缩、特征提取、数据可视化等[^4]。 ---
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值