【数据结构基础整理】图--03：十字链表，邻接多重表

具体实现十字链表和邻接多重表的代码

0x01.十字链表

由来：

邻接表只适合对某个顶点的出度相关信息进行判断，逆邻接表只适合对入度的相关信息进行判断，当同时需要判断的时候，就需要引入一种新的结构：十字链表。

为什么叫十字链表？

首先来看一下十字链表的顶点结构：

data指顶点的数据域；firstin表示顶点第一个指向由顶点作为弧头的弧（顶点为终点）；firstout表示顶点第一个指向由顶点作为弧尾的弧（顶点为弧的起点）。

然后看一下边表结构：

tailvex指该弧的弧尾的所在数组下表；headvex指该弧的弧头所在数组的下标；headlink是指向起点相同的下一条边；taillink是指向终点相同的下一条边；info也可叫wight，记录边的权值。

从一个顶点开始，可以选择firstin指针，开始指向边，然后到某一条具体的边，又可以选择是指向起点相同的下一条边，还是指向终点相同的下一条边，每进一条路有多个选择，像一个十字，故称之为十字链表。

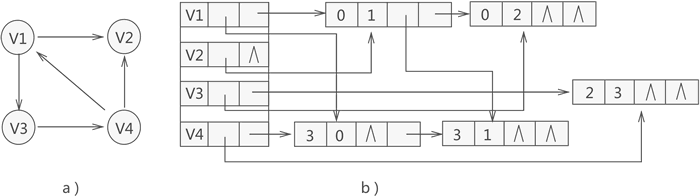
注意：十字链表只适用于有向图。

十字链表结构：

#define MAXSIZE 100

//边表结构
typedef struct EdgeNode
{
	int tailvex;//弧起点在顶点表中的下标
	int headvex;//弧终点在顶点表中的下标
	struct EdgeNode* headlink;//指向起点相同的下一条边
	struct EdgeNode* taillink;//指向终点相同的下一条边
	int weight;//存储权值
}EdgeNode;

//顶点表结构
typedef struct VexNode
{
	char data;//顶点数据域
	EdgeNode* firstin;//以该顶点为弧终点（弧头）的边表头指针
	EdgeNode* firstout;//以该顶点为弧起点（弧尾）的边表头指针
}VexNode,VexList[MAXSIZE];//同时创建了一个顶点表数组

//十字链表图结构
typedef struct
{
	VexList vexlist;//顶点表
	int numv;//顶点数
	int nume;//边数
}OLGraph;

十字链表创建：

void CreateOLGraph(OLGraph* G)
{
	int i, j, k, w;
	printf("请输入图的顶点数和边数：\n");
	scanf("%d %d", &G->numv, &G->nume);
	while (getchar() != '\n');//清空缓冲区
	for (i = 0; i < G->numv; i++)//录入顶点信息
	{
		scanf("%c", &G->vexlist[i].data);
		G->vexlist[i].firstin = NULL;//初始化
		G->vexlist[i].firstout = NULL;
	}
	for (k = 0; k < G->nume; k++)//录入边信息
	{
		printf("请输入弧的起点在数组中的下标，终点在数组中的下标，和权值:\n");
		while (getchar() != '\n');//清空缓冲区
		scanf("%d %d %d", &i, &j, &w);
		EdgeNode* e = (EdgeNode*)malloc(sizeof(EdgeNode));
		e->tailvex = i;
		e->headvex = j;
		e->weight=w;
		e->headlink = G->vexlist[j].firstin;//头插法
		e->taillink = G->vexlist[i].firstout;//头插法
		G->vexlist[j].firstin = e;
		G->vexlist[i].firstout = e;
	}
}

十字链表的普通遍历：

void PrintOLGraph(OLGraph G)
{
	for (int i = 0; i < G.numv; i++)
	{
		EdgeNode* p = G.vexlist[i].firstin;
		printf("以顶点 %c 为头的边有：\n", G.vexlist[i].data);
		int numhead = 0;//记录入度数
		while (p)
		{
			printf("顶点 %c 到顶点 %c ，权值为 %d \n",G.vexlist[p->tailvex].data,G.vexlist[p->headvex].data,p->weight);
			numhead++;
			p = p->headlink;
		}
		printf("该顶点的入度为 %d \n", numhead);
		printf("以顶点 %c 为尾的边有：\n", G.vexlist[i].data);
		int numtail = 0;//记录出度数
		p = G.vexlist[i].firstout;
		while (p)
		{
			printf("顶点 %c 到顶点 %c ，权值为 %d \n", G.vexlist[p->tailvex].data, G.vexlist[p->headvex].data, p->weight);
			numtail++;
			p = p->taillink;
		}
		printf("该顶点的出度为 %d \n", numtail);
	}
}

0x02.邻接多重表

由来：

十字链表是对于有向图的优化，对于无向图的邻接表来说，如果我们更关注对已访问过的边做标记，删除边等关于边的操作，那么我们需要用到邻接多重表。

顶点表结构图示：

顶点结构和邻接表一样，data指数据域；firstedge指第一条指向的边。

边表结构图示：

mark：作为标志变量，用于记录此边的结点是否被访问过；
ivex：记录边一端在顶点数组中的下标；
jvex：录边另一端在顶点数组中的下标；
ilink：指针，指向与 i 端相关联的下一条边；
jlink：指针，指向与 j 端相关联的下一条边；

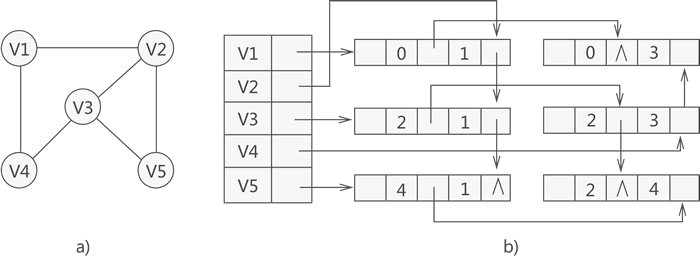
结构：

#define MAXSIZE 100

//边表结构
typedef struct EdgeNode
{
	int mark;//标志域 0 为未访问过 1 为访问过
	int ivex;//边的 i 端
	int jvex;//边的 j  端
	struct EdgeNode* ilink;//指向和  i  相关的边
	struct EdgeNode* jlink;//指向和  j  相关的边
	int weight;
}EdgeNode;

//顶点表结构
typedef struct VexNode
{
	char data;
	struct EdgeNode* firstedge;
}VexNode,AdjList[MAXSIZE];

//邻接多重表结构
typedef struct
{
	AdjList adjlist;
	int numv;
	int nume;
}AMLGraph;

邻接多重表创建：

void CreateAMLGraph(AMLGraph* G)
{
	int i, j, k, w;
	printf("请输入图的顶点数和边数：\n");
	scanf("%d %d", &G->numv, &G->nume);
	while (getchar() != '\n');//清空缓冲区
	for (i = 0; i < G->numv; i++)
	{
		scanf("%c", &G->adjlist[i].data);
		G->adjlist[i].firstedge  = NULL;//初始化
	}
	for (k = 0; k < G->nume; k++)
	{
		printf("请输入边的两顶点在数组中的下标和边的权值:\n");
		while (getchar() != '\n');//清空缓冲区
		scanf("%d %d %d", &i, &j, &w);
		EdgeNode* e = (EdgeNode*)malloc(sizeof(EdgeNode));
		e->mark = 0;
		e->ivex = i;
		e->jvex = j;
		e->weight = w;
		e->ilink = G->adjlist[i].firstedge;
		e->jlink = G->adjlist[j].firstedge;
		G->adjlist[i].firstedge = e;
		G->adjlist[j].firstedge = e;
	}
}

普通遍历邻接多重表：

void PrintAMLGraph(AMLGraph G)
{
	for (int i = 0; i < G.numv; i++)
	{
		EdgeNode* p = G.adjlist[i].firstedge;
		printf("和顶点 %c 有关的边有：", G.adjlist[i].data);
		while (p)
		{
			if (p->ivex == i)//判断时边的何端与 i 相等
			{
				//if (p->mark == 1)//当某条边是需要访问一次时采用标志变量，否则不用
				//{
					printf("%c 到 %c ，权值为 %d\t", G.adjlist[p->ivex].data, G.adjlist[p->jvex].data, p->weight);
					//p->mark = 1;
				//}
				p = p->ilink;
			}
			else
			{
				//if (p->mark == 0)
				//{
					printf("%c 到 %c ，权值为 %d\t", G.adjlist[p->jvex].data, G.adjlist[p->ivex].data, p->weight);
					//p->mark = 1;
				//}
				p = p->jlink;
			}
			printf("\n");
		}
	}
}