助你稳过高校离散结构 --（系列一）-CSDN博客

0x01.说明

离散数学其实是计算机领域一门比较重要的学科，对某些算法，底层原理的研究起到了非常重要的作用。
离散结构是逻辑学，集合论（包括函数），数论基础，算法设计，组合分析，离散概率，关系理论，图论与树，抽象代数（包括代数系统，群、环、域等），布尔代数，计算模型（语言与自动机）等汇集起来的一门综合学科。
如果以后的你想要深究其中某个领域，它一定是必不可少的工具，如果不去探讨这些，其实也可以稍作了解，重要的是，现在高校的计算机专业中，大都会有这门课程，所以，还是好好学一学吧。
本文对高校中需要的离散结构知识做一些总结，也许，对期末正复习的你有帮助哦！

0x02.逻辑与证明

1.命题：

一个命题就是一个陈述句，陈述的事情需要能够判别真假。
- 注意1：要么真，要么假，不能又真又假。
- 注意2：陈述句，能判断真假，缺一不可。
- 注意3：悖论不是命题。
- 注意4：在判断命题真假时，需要明确其所在的场景（表述的上下文）。
  - 例如：x+2=3不是命题，但如果进行赋值x=1，就是命题了。
命题的真假叫做命题的真值。
- 真值可以表示为：【True，False】 或 【0，1】
- 真值表：枚举复合命题中，所有命题变量的所有真值情况。（如否定命题的真值表）
原子命题：其真假独立于其它命题的最小命题。
- 原子命题是数理逻辑的基本单位。
- 原子命题的符号化表示：
  - 一般使用小写字母，如p，q，r，s表示命题变量。

2.逻辑运算符：

用于组合命题的符号，表示原子命题之间的逻辑关系，也叫逻辑联接词。
基本逻辑运算符：
- 否定（非）：
- 合取（且）：【同为真时且为真】
- 析取（或）：【同为假时或为假】
- 异或：【当且仅当一个为真时异或为真】
复合命题：已有命题用逻辑运算符组合成的新命题。
- 永真式：重言式。
- 矛盾式：永假式。
- 可能式：有真有假。（可满足性）

3.条件语句–蕴涵：p→q 【p真q假才为假，否则则为真】

p：表示假设、前项、前提。
q：表示结论、推论。
语义化：【如果 p，则 q】，【p 推出q】，【p 仅当q】，【只有 q，才有p】，【q 当 p】。
蕴含的逆：
蕴含的反：
蕴含的逆否：

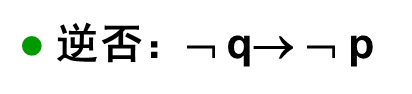
4.双条件语句–双蕴涵：

在这里插入图片描述

p、q之间互为充要条件。

5.逻辑运算符的优先级：

在这里插入图片描述

6.系统规范

每条规范说明，就是一个命题。
规范集合是一致的。
- 全部规范都能够得到满足。
- 全部对应命题真值都为真。
判断系统是否规范的核心：【存在一组命题的赋值，使得全部命题都为真】

7.逻辑等价：

在这里插入图片描述

证明命题等价的方法：真值表、恒等式变换
- 真值表：画出两个命题的真值表，如果对应真值情况完全相同，则等价。
- 恒等式变换：通过已知的恒等式变换，最终由一个命题变换成了另一个命题。
重要逻辑等价式：
- 恒等率：
- 支配率：
- 幂等率：
- 双重否定率：
- 否定率：
- 交换律：
- 结合律：
- 德.摩根律:
- 分配率：
与蕴含有关的等价：

List item 在这里插入图片描述

双蕴含有关等价式：
利用恒等式证明逻辑等价的核心思路：【努力让左边变得向右边（或者右边像左边），差什么，用什么公式去构造】

8.谓词

含变量的陈述句不能直接表示成命题，当我们把这个命题看成一个函数时，通过变量赋值，含变量的陈述句就能直接表示成命题。这个函数称为命题函数。
- 注意1：命题函数不是命题！
- 注意2：变量赋值后，就是命题。
谓词：在命题函数中，表明变量具有的性质。
定义域（论域）+ 取值范围+ 命题函数= 命题
例如：命题函数P(x): x＞3 不是命题，P(4)、P(2) 是命题。

9.量词

在这里插入图片描述

论域：变量的取值范围，全总论域= { 万事万物}。
排中律：对任何事物在一定条件的判断都必须有明确的“是”或“非”，不存在中间状态。【不能证明是假就是真】
量词后面有条件就是约束论域的量词。
量词的优先级:
含量词的逻辑等价式：

在这里插入图片描述

量化命题的否定：
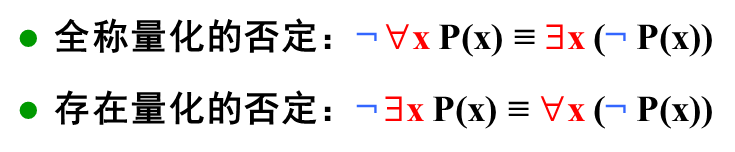
量词的顺序：
- 相同类型量词嵌套时，顺序不重要，顺序的交换，不会影响命题的含义。
- 不同类型量词交叉嵌套，顺序很重要。顺序不同，命题的含义不同。
否定嵌套量词：从外向内连续应用否定，直到所有的量词前没有否定。

10.证明与推理

证明：建立数学命题真实性的有效论证。
论证：一个命题序列。
论证是有效的：若所有前提为真，则结论必真。
证明方法：
- 直接证明法：p→q
  - ① 假定p 为真
    ② 结合已知成果(定义+公理+定理)＋推理规则
    ③ 推出q 为真
- 间接证明：p→q ≡ ¬q→¬p
  - 假定 ¬q 为真，推出¬p。
- 归谬法(反证法)
  - 要求证明p 为真，假设 ¬p 为真，在上述假设下，若能推导出矛盾式，则p为真。
- 空证明：前提为假，蕴涵式自动为真。
- 平凡证明：结论已为真，蕴涵式自动为真→无需前提为真
- 分情形证明法：每个子前提与结论构成一种情形。
- 穷举证明：枚举所有可能情况。
- 唯一性证明：存在性＋唯一性。

0x03.集合

1.集合的表示方法

列举法：直接枚举所有(或部分)的元素。
构造法：用谓词描述所有元素的性质。

在这里插入图片描述

文氏图。

2.集合与元素

集合与元素的关系：成员关系。
元素的性质：确定性、无序性、相异性、嵌套性。

3.集合与集合的关系

相等：

在这里插入图片描述

包含：
真包含：
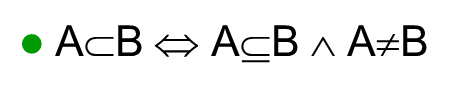
空集：不含有任何元素得到集合
- 注意1：空集是任何集合的子集
- 注意2：空集是唯一的

4.基数和幂集

基数是集合 S 的元素个数，记为|S|
幂集：
- 举例：
如果 |S|=n，则 |P(S)|=2^n
全集 U：所有元素组成的集合。

5.笛卡尔积

在这里插入图片描述 - 例如：

在这里插入图片描述

笛卡尔积不满足交换律。

6.集合间的运算

并：

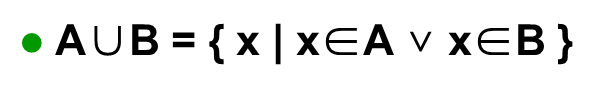
在这里插入图片描述

交：

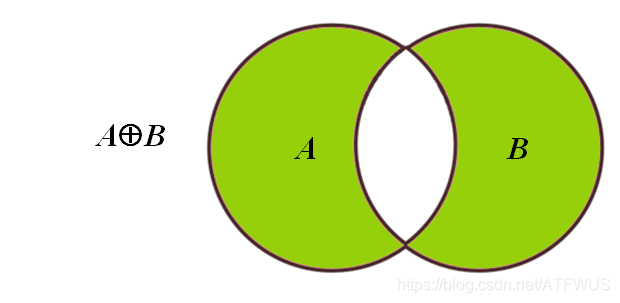
在这里插入图片描述

差：

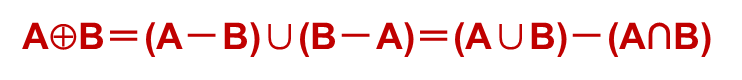
在这里插入图片描述

对称差：

在这里插入图片描述

补：

在这里插入图片描述

运算优先级：

7.集合恒等式

在这里插入图片描述

证明集合恒等式的方法：
- 方法一：集合相等定义法【在集合A中任取元素x，通过推理和变换，证明x属于B】
- 方法二：集合构造定义法【将集合A表式成构造式，通过变换，表示成集合B的构造式】
- 方法三：成员表法【列举两个集合的成员表，完全一致则相等】
- 方法四：集合恒等式变换法【通过集合恒等式的变换证明两个集合相等】