对不知情感到愤怒[Outraged by not knowing]

翻译过程中如果存在问题，欢迎大家指正。

简要总结：奥斯卡·兰德尔-威廉姆斯从事的是拓扑学领域——这一数学领域研究在允许弯曲、拉伸或压缩对象，但不切割或撕裂的情况下，哪些属性保持不变。他非常接近回答关于欧几里得空间的基本问题——这些空间就是你在学校里学到的，可以通过坐标轴来确定的最基本的拓扑空间。他和他的同事们认为他们找到了一种方式，最终完成对欧几里得空间所有对称性的描述。

当你第一次了解数学时，它可能看起来像是一个坚固的知识堡垒——完整且不变。但有时候，即使是基本问题也仍然没有答案，而当这样的答案可能就在眼前时，总是非常激动人心的。我们很幸运能够与我们在剑桥大学数学科学中心的邻居奥斯卡·兰德尔·威廉姆斯进行交谈，他非常接近这样的答案。

兰德尔-威廉姆斯从事的是拓扑学——数学的一个领域，研究在允许弯曲、拉伸或压缩对象，但不切割或撕裂的情况下，哪些属性保持不变。众所周知，一个有中间洞的甜甜圈在拓扑上与一个咖啡杯相同——如果它们都是由可塑性黏土制成的，你可以将一个弯曲和拉伸成另一个。但它们与球体在拓扑上不同——你不能不通过撕裂或切割就将一个球体变成一个甜甜圈。

这些——甜甜圈、咖啡杯和球体（或更准确地说是这些的表面）——都是拓扑空间的例子。但在拓扑学中最基本的空间是你在学校学过的空间——欧几里得空间。这些是最具体的空间，通过一些坐标轴（如你在学校绘图时使用的垂直和水平轴）来确定。你的空间的维度由你需要映射它的坐标轴数量给出。兰德尔-威廉姆斯正试图回答的问题是：欧几里得空间，特别是五维或更高维度空间的对称性是什么？

Topology in action

平滑对称性

旋转，连同反射，是我们本能想到的对称性，但当应用于欧几里得空间时，这意味着什么呢？考虑我们都熟悉的三维欧几里得空间，它有两个垂直的水平轴（用于前后和左右）和一个垂直轴。然后，该欧几里得空间中的每个点都用这三个轴来表示。比如说，围绕某个旋转轴将这三个轴旋转45度，空间本质上保持不变。例如，一切仍然相距相同的距离，坐标轴仍然是彼此垂直的直线。旋转作为欧几里得空间的一种对称性。

旋转和反射及其向更高维度的推广，被称为平滑对称性。我们可以通过将它们想象为在某个空间中的点来思考所有这些平滑对称性之间是如何相关的。你可以想象从上面描述的旋转开始，在这个对称性空间中轻微移动。这可能会带你到一个略微多于或少于45度的旋转，或者是旋转轴稍微移动了一点的旋转。“那么那是一个类似的旋转——它不相同，但它与你之前的旋转相近，”兰德尔-威廉姆斯说。“考虑在对称性空间中行走是有意义的。”对于欧几里得空间的平滑对称性空间，大约一个世纪以来已经被很好地理解了——数学家们已经用它的拓扑来描述了这个空间。

连续对称性

但还有另一种对称性，称为连续对称性，与平滑对称性相比，它要难以理解得多：“你不能真正直接思考连续对称性，这有点像直视太阳一样！”连续对称性难以想象。像平滑对称性一样，连续对称性也必须将临近点映射到临近点。但它们可能表现得更为奇特，比如，它们可以将一个轴映射到某个非常崎岖的曲线上。

不能直视太阳！而且你不能真正直接思考连续对称性！

2019 年 12 月 26 日从斯里兰卡贾夫纳看到的日环食。雷曼·阿布巴克尔摄

连续对称性的空间包括所有的平滑对称性，但数学家自1970年代以来就已知道存在一些不是平滑的连续对称性。但到目前为止，我们还没有欧几里得空间的连续对称性空间的描述。

对于数学家来说，包括兰德尔-威廉姆斯在内，描述欧几里得空间的所有对称性，而不仅仅是平滑对称性，是一个基本问题。“我的主要动力是对不了解事物感到愤怒！”他说。“这是如此根本的一件事，是我们对这些空间的对称性意味着什么的一种真正基本的理解。”

欧几里得空间可以被认为是拓扑学中最基本的案例，拓扑学更广泛地处理流形（即，任何在局部看起来像欧几里得空间的东西）。“所以，如果你能回答欧几里得空间的问题，你就在回答更多问题的道路上。”

兰德尔-威廉姆斯和他的同事们现在正濒临为每一个维度为5或以上的欧几里得空间的连续对称性提供一个完整的描述。“我们还没有完全详细地证明它，但它内在逻辑如此充分，我相信它一定是正确的。”

重新表述问题

由于直接考虑连续对称性非常困难，兰德尔-威廉姆斯及其同事亚历山大·库珀斯和曼努埃尔·克兰尼希找到了一种重新表述这个问题的方法。结果表明，理解欧几里得空间的连续对称性与理解一个圆盘（在二维中是圆内区域的数学名称，以及这个概念向更高维度的推广）的平滑对称性或多或少是可以互换的。

通过这种新的视角，兰德尔-威廉姆斯及其同事能够发展并找到他们猜想的有力证据：任何高维欧几里得空间的连续对称性空间可以用称为图复形的代数对象来表示。

图复形在过去的10到15年里才真正被详细研究。（我们现在讨论的是另一种数学图——这种图你通常可能会称为网络。）“它们是由图构建的——就是点和连接它们的线的意义上，”兰德尔-威廉姆斯说。图复形是由有限图构建的——具有有限数量的点（节点）和连接它们的线（边）的图——和一个捕捉收缩边的所有方式的操作。

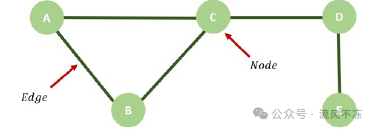
具有五个节点和五个边的网络（或图）

兰德尔-威廉姆斯说，这些图复形之所以令人难以置信的是它们非常基础。上面的定义很模糊，但即便是一个严谨的数学定义对于数学家来说也出奇地容易表述。“而且相同的图复形在数学的极其不同领域中出现。我说的不仅仅是相同类型的东西，我是指字面上的相同图复形。”

惊人的联系

他在欧几里得空间对称性工作中出现的图复形也在数学物理中出现（这是图复形首次出现的领域），并且与数学其他领域的问题相关，如代数几何（使用代数研究几何的数学领域）。“这真是不可思议，确实是同一个[图复形]回答了这些不同的问题。特别是，这表明那些问题在某种方式上是相关的，因为它们都与同一个小的组合对象相关。”但如果不考虑图复形，很难看出这些数学领域之间是如何相关的。“这确实是某种原始的东西。就像质数一样——它是出现在许多不同建筑中的构建块。”

图复形提供了兰德尔-威廉姆斯及其同事所寻找的描述这一事实相当令人惊讶。“联系相当间接。为什么欧几里得空间的对称性应该与有限图有任何关系？这一点一点都不明显。”他们现在正在与图复形世界专家托马斯·威尔瓦彻合作，进行下一步的工作以证明他们的猜想。敬请关注——我们将会及时更新他们在拓扑学这一基本问题上的证明进展！

Oscar Randal-Williams

关于这篇文章

奥斯卡·兰德尔-威廉姆斯是剑桥大学的萨德勒纯数学教授。你可以在他参加2022年国际数学家大会的论文、他与曼努埃尔·克兰尼希在2021年的论文，以及他与亚历山大·库珀斯在2024年1月的论文中找到关于本文探讨的工作的一些数学细节。

原文：https://plus.maths.org/content/outraged-not-knowing